K-SVD

breeze5428

于 2014-09-06 11:11:46 发布

阅读量1w

点赞数 7

分类专栏：机器学习数学文章标签： KSVD 字典 SVD sparse coding 稀疏

本文链接：https://blog.csdn.net/breeze5428/article/details/24964031

版权

K-SVD是一种字典学习算法，用于稀疏表示问题，是K-means的推广。它通过迭代优化数据在字典中的表示和更新字典，广泛应用于图像、语音等领域。算法首先固定字典求最佳系数，然后更新字典的每一列，利用SVD进行优化。尽管存在非凸优化问题导致局部最优，但在实践中表现良好。

摘要由CSDN通过智能技术生成

参考网址：http://en.wikipedia.org/wiki/K-SVD

K-SVD 是一种关于稀疏表示的字典学习算法。之所以称之为K-SVD ，是因为该算法K次迭代使用SVD（singular value decomposition）。K-SVD是 k-means的一种推广，该算法采用迭代交替学习方式，通过迭代优化输入数据在当前字典的表示和更新字典中的单词（atom）以更好地拟合数据^1]^[2] 。 K-SVD在图像处理、语音处理、生物和文件分析等众多领域被广泛应用。

稀疏表示问题描述

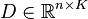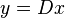给定一个过完备的字典 $D \in \mathbb{R}^{n \times K}$ ，该字典包含 $K$ 个单词，在此每一列都被视作一个单词。一个信号 $y \in \mathbb{R}^{n}$ 能够被表示为这些单词的线性组合。为表示 $y$ ，稀疏表示 $x$ 应当满足精确条件 $y = Dx$ , 或者满足近似条件 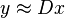$y \approx Dx$ , 或者满足条件 $\|y - Dx\|_p \le \epsilon$ . 向量 $x \in \mathbb{R}^{K}$ 由表示 $y$ 的系数组成. 通常来说, 范数