动态规划(DP)---LCS(the Longest Common Subsequence)

0 暴力求解两个序列的最长公共子序列(LCS)

$string \quad x$: B D C A B A
$string \quad y$: A B C B D A B

字符串 $x\quad y$ 的几个最长公共子序列是这个样子的:

$$BDAB \quad BCBA\quad BCAB$$

第一次遇到这种题时，我会不假思索地将字符串 $x \quad y$ 所有的子序列找出来，然后一个个地比较来找出它们的最长子序列（LCS）。那么问题来了，一个长度为 $m$ 的字符串到底有多少个子序列呢？

$$含\quad 1 \quad个字符的子串有 \quad C_m^1 \quad个子串$$

$$含\quad 2 \quad个字符的子串有 \quad C_m^2 \quad个子串$$
$$含\quad 3 \quad个字符的子串有 \quad C_m^3 \quad个子串$$
$$.....$$
$$含\quad m \quad个字符的子串有 \quad C_m^m \quad个子串$$

子序列的个数为: $C_m^1 + C_m^2+C_m^3+...+C_m^m$

这个跟二项展开式很像，二项展开式是这个样子的：

$$(a+b)^m = C_m^0a^m + C_m^1a^{m-1}b^1+C_m^2a^{m-2}b^2+...+C_m^ra^{m-r}b^r+...+C_m^mb^m$$

所以，一个长度为 $m$ 的字符串一共有 $2^m-1$ 个子序列。

那么，使用暴力的方式，找出两个长度分别为 $m, n$ 的字符串的 LCS 的时间复杂度是多少呢？

$$1st,\quad 找出两个字符串的所有子序列:\quad=>\quad 2^m-1+2^n-1=\Theta(2^m+2^n)$$
$$2nd, \quad 将各自的所有子序列两两比较:\quad=>\quad (2^m-1)\times(2^n-1) = \Theta(2^{m+n})$$
由此，暴力破解的时间复杂度就是： $$\Theta(2^m+2^n)+\Theta(2^{m+n})=\Theta(2^{m+n})$$
如何？暴力破解所消耗的时间是 指数规模（exponential time）的，这样的速度就是龟速！

---

1 动态规划（Dynamic Programming）

动态规划通常用来求解最优化问题（optimization problem）。这类问题可以有很多可行解，每个解都有一个值，我们希望寻找具有最优值（最小值或最大值）的解。我们称这样的解为问题的一个最优解（an optimal solution），而不是最优解（the optimal solution)，因为可能有多个解达到最优值。

我们通常按如下4个步骤来设计一个动态规划算法：

1，刻画一个最优解的结构特征。
2，递归地定义最优解的值。
3，计算最优解的值，通常采用自底向上的方法。
4，利用计算出的信息构造一个最优解。

————自《算法导论》机械工业出版社

并不是所有的最优问题都可以使用动态规划来求解，使用动态规划必须满足两个问题：

1. 最优子问题（optimal subproblems）。
2. 重叠子问题（overlapping subproblems）。

---

2 使用动态规划求解LCS

按照上面提到的4个步骤来设计一个求解LCS的动态规划算法。

2.1 刻画一个最优解的结构特征

定义：

$$c[i,j] = |LCS(x[1...i],\quad y[1...j])|\quad \quad......(1)$$
$c[i,j]$ 为字符串 $x[1...i]$ 和 $y[1...j]$ 的 LCS 的长度。

那么：

$$c[m,n] = |LCS(x,\quad y)|\quad m,n\quad 为字符串\quad x,y\quad的长度$$
因此，LCS 最优解的结构特征就是 $c[m,n]$。

2.2 递归定义最优解的值

根据2.1定义的最优解的结构特征，写出 $c[i,j]$ 的归纳表达式如下：

$$c[i,j]= \begin{Bmatrix} c[i-1,j-1]+1 & if\quad x[i]==y[j]\\ max\{c[i-1,j], \quad c[i,j-1]\} & otherwise \end{Bmatrix}\quad \quad......(2)$$
下面证明式(2)的正确性。

     $if\quad x[i]==y[j]$

$$令\quad z[1...k]\quad 等于\quad LCS(x[1...i],y[1...j])，那么\quad c[i,j]=k\quad且\quad z[k]=x[i]=y[j]$$
$$z[1...k-1] = LCS(x[1...i-1],y[1...j-1])\quad c[i-1,j-1]=k-1$$
$$假设存在一个公共子序列\quad w=CS(x[1...i-1],y[1...j-1]),\quad 其长度\quad |w|>k-1，使用w后接z[k]组成一个新序列，则新序列的长度\quad c[i,j]=|w,z[k]|>k，这与之前的\quad c[i,j]=k\quad 相矛盾！这种证明方法就是 Cut Copy方法$$

     $other\quad x[i]!=y[j]$证明略。

2.3 计算最优解的值，通常采用自底向上

2.3.1 自顶向下

参照归纳表达式(2)，写出LCS递归算法如下：

LCS(x,y,i,j)
if x[i] == x[j]
    c[i,j]=LCS(x,y,i-1,j-1)+1
else
    c[i,j]=max(LCS(x,y,i-1,j),LCS(x,y,i,j-1))
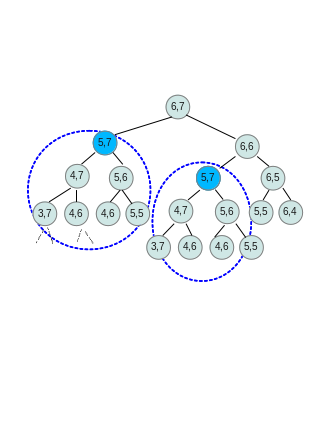
return c[i,j]

在最坏情况下，即 $x[i]!=y[j]$，参数$string \quad x, \quad y$ 的部分递归树，如下：

递归树的高度为：$m+n=13\quad$ m,n为两个字符串的长度。根据满二叉树的性质，知道高度 $h$，就可以算出二叉树节点的总数为$2^h-1$，从上面的递归树可以知道，一个节点就是一个子问题，那么算法的时间复杂度有一个渐进紧确上界为：$O(2^{m+n})$。

由蓝色虚线框出的部分可以看出，递归算法存在重复运算，这也验证了动态规划的第二个特征：重叠子问题。
改进算法，将子问题的解存储起来（备忘法），下次求解相同子问题时直接取出解：

LCS(x,y,i,j)
if c[i,j]!=nil
    return c[i,j]
if x[i] == x[j]
    c[i,j]=LCS(x,y,i-1,j-1)+1
else
    c[i,j]=max(LCS(x,y,i-1,j),LCS(x,y,i,j-1))
return c[i,j]

使用备忘法后，独立子问题的规模就只有 $m\times n$，相应的时间复杂度为 $\Theta(m\times n)。$
那么，独立子问题的规模是怎么知道的呢？答案就在算法中的数组$c[i,j]$，整个算法就是在填充二维数组$c$，所以独立子问题的规模就等于二维数组$c$的大小 $m\times n$。

2.3.2 自底向上(bottom-up)

从前面的自顶向下可以看出，算法有很多的重复计算，虽然采用备忘法可以去掉重复，但是程序极为不清晰。一般来说，真正的动态规划更多的是采用自底向上的方法来去重复。

参照式（2）归纳式，可以很容易地写出自底向上的伪代码，其求解方法就是自底向上填充数组$c$：

LCS（x,y,m,n)
for i=0 to m-1
    for j=0 to n-1
        if x[i]=y[j]
            c[i,j]=c[i-1,j-1]+1
        else 
            c[i,j]=max(c[i-1,j],c[i,j-1])
return c[m,n]
//代码没有考虑 c[-1,-1]，由于 c[-1,-1]没有任何前缀字符，所以 c[-1,-1]=0, c[-1,*]=c[*,-1]=0

根据代码来填充数组 $c$，如下图所示：

如图所示，蓝色边框就是计算后的数组$c$，在 $c$ 中，红色元素为上面代码中满足 $x[i]=y[j]$ 的情形，蓝色情况为不满足情形。

2.4 利用计算出的信息构造一个最优解

那么利用数组 c <script type="math/tex" id="MathJax-Element-50">c</script> 的信息如何找出真正满足LCS的条件呢？