一、线性筛
namespace G
{
bool vis[_+10];
int pnt,pri[_+10],phi[_+10],miu[_+10];
void go()
{
phi[1]=miu[1]=1;
for(int i = 2;i <= _; i++)
{
if(!vis[i])
{
pri[++pnt] = i;
phi[i] = i-1;
miu[i]=-1;
}
for(int j=1; j<=pnt && i*pri[j]<=_; j++)
{
vis[i*pri[j]]=1;
if(i%pri[j]==0)
{
phi[i*pri[j]] = phi[i] * pri[j];
miu[i*pri[j]] = 0;
break;
}
else
{
phi[i*pri[j]] = phi[i] * (pri[j]-1);
miu[i*pri[j]] = -miu[i];
}
}
}
for(int i=1;i<=25;i++)printf("%d %d\n",i,miu[i]);
}
}二、积性函数
d是n约数 ∑ φ(d) = n
d与n互质 ∑ d = n * φ(n) / 2
莫比乌斯 μ(n) = (-1) ^ k [ n = p1 p2 ... pk , k distinct primes ]
d是n约数 ∑ μ(d) = [ n = 1 ]
φ(n) = ∑ (-1) ^ k * n / (p1 p2 ... pk) = ∑ μ(d) * n / d
反演 F(n) = ∑ f(d) 那么 f(n) = ∑ F( n/d ) * μ(d)三、例题
【题目1】
【题目2】
【题目3】








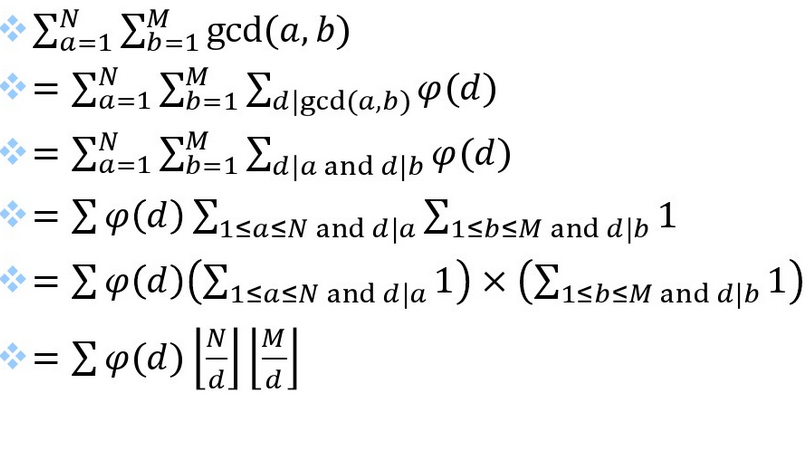
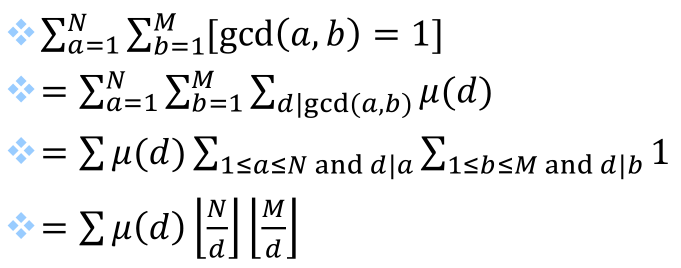














 3379
3379

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








