数据分布类型及处理方式

数据类型

1. 离散型数据：固定取值，值的数量是有限的
   随机变量$X$的分布律为：$P(X=x_i)=p_i,i=1,2,\cdots$,期望和方差如下
   $$E(x)=\sum _i{x}_i{p}_i,D(x)=\sum _i(x_i-E(x){)}^2{p}_i$$
2. 连续性数据：在给定范围内有无数取值
   $$E(x)={\int }_a^{b}xf(x)dx,D(x)={\int }_a^b(x-E(x){)}^{2}f(x)dx$$
   其中，$f(x)$表示随机变量的概率密度函数
   期望和方差的关系：（$E(x)$为常数，则$E[E(x)]=E(x)$）
   $$D(x)=E([x-E(x){]}^2)=E(x^2-2xE(x)+E(x{)}^2)=E(x^2)-2[E(x){]}^2+[E(x){]}^2=E(x^2)-[E(x){]}^2$$

期望和方差性质

期望：
来量化一个随机变量可能的平均水平。在实际应用中，期望常常被用来预测未来可能发生的平均情况

1. 设 $C$是常数，则有 $E(C)=C$
2. 设$X$是一个随机变量，$C$是常数，则有 $E(CX)=CE(X)$
3. 设$X,Y$ 是两个随机变量，则有 $E(X+Y)=E(X)+E(Y)$
4. 设 $X,Y$ 是相互独立的随机变量，则有 $E(XY)=E(X)E(Y)$

方差：
用来衡量随机变量或一组数据离散程度的度量。在实际应用中，方差常常被用来描述数据的波动性

1. 设 $C$是常数，则 $D(C)=0$
2. 设$X$是随机变量，$C$是常数，则有 $D(CX)=C^{2}D(X),D(X+C)=D(X)$
3. 设$X,Y$是两个随机变量，则有$D(X+Y)=E([(X+Y)-E(X+Y){]}^2)=D(X)+D(Y)+2E[(X-E(X))(Y-E(Y))]$，特别，若$X,Y$相互独立，则有 $D(X+Y)=D(X)+D(Y)$
4. $D(X)$的充要条件是$X$以概率 1 取常数$E(X)$，即 P { X = E ( X ) } = 1 P\{X=E(X)\}=1 P{X=E(X)}=1

数据分布类型

正态分布

正态分布，也称为高斯分布，是一种在数学、物理及工程等领域都非常重要的概率分布。在统计学中，正态分布的数据形态呈现为钟型，两头低，中间高，左右对称。
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-u{)}^2}{2{\sigma }^2}},-\infty <x<\infty$$
$$E(X)=\mu ,D(x)={\sigma }^2,X\sim N(\mu ,\sigma )$$

标准正态分布的均值为$0$,方差为$1$，密度为$f(x)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}$

处理方法：正态分布是许多统计模型的基础，如果数据不符合正态分布，可以通过对数变换、平方根变换等方法尝试将其转化为正态分布。

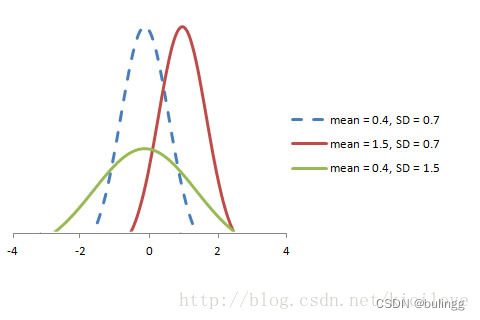
均匀分布

均匀分布是最简单的概率分布，它的所有值在相同长度的间隔内出现的概率是相等的。
$$f(x)=\frac{1}{b-a}$$
$$E(x)={\int }_a^{b}xf(x)dx={\int }_a^b\frac{x}{b-a}dx=\frac{a+b}{2}$$
$$D(x)={\int }_a^b(x-E(x){)}^{2}f(x)dx$$
处理方法：均匀分布通常不需要特殊处理，但如果需要，可以通过分箱、离散化等方法进行处理。

二项分布

二项分布是一种离散概率分布。它描述了在一系列独立的是/非试验中成功的次数的概率分布，其中每次试验的成功概率为p。
重复$n$次实验，每次实验都是独立的，实验成功$x$的概率为
$$p(x)=C_n^x{p}^x(1-p{)}^{n-x}=\frac{n!}{(n-x)!x!}{p}^x(1-p{)}^{n-x}$$
$E(x)=np,D(x)=np(1-p)$
处理方法：二项分布通常用于分类问题中，可以通过逻辑回归、决策树等模型进行处理。
$p!=0.5$时：

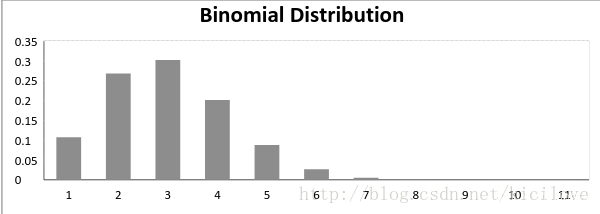
$p=0.5$时：

泊松分布

泊松分布是一种离散概率分布，描述了在固定时间或空间内发生的事件的次数的概率分布。

1. 任何成功的事件都不应该影响另一个成功事件的结果。
2. 在较短的时间间隔内成功的概率必须等于在较长的时间间隔内成功的概率。
3. 随着间隔变小，间隔内成功的概率接近零
   $$P(X=x)=e^{-u\frac{{\mu }^x}{x!}},x=0,1,2,\cdots$$
   $$E(x)=\mu ,D(x)=\mu$$
   其中，

• $\mu$表示时间$t$内事件发生的平均次数，$\mu =\lambda t$,
• $\lambda$表示时间发生的速率，
• $t$表示时间间隔长度
• $X$表示时间间隔$t$内时间发生的次数
  处理方法：泊松分布通常用于计数数据的模型，如泊松回归。
  

指数分布

指数分布是一种连续概率分布，可以用来表示独立随机事件发生的时间间隔。
$$f(x)=\lambda e^{\lambda x},x\ge 0$$
$$E(x)=\frac{1}{\lambda },D(x)=\frac{1}{{\lambda }^x}$$
其中，$\lambda$表示速率，速率越大，曲线下降越快，速率越低，曲线越平滑

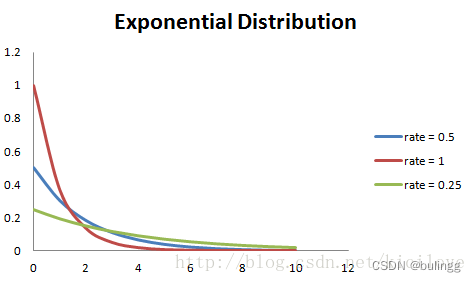
处理方法：指数分布通常用于生存分析或者可靠性分析的模型。

对数正态分布

对数正态分布是一种连续概率分布，如果一个随机变量的对数服从正态分布，那么该随机变量就服从对数正态分布。
$$log(x)\sim N(\mu ,\sigma )$$

处理方法：对数正态分布的数据可以通过对数变换转化为正态分布，然后使用基于正态分布的统计模型进行处理。

分布之间关系

1. 伯努利分布与二项分布

• 伯努利分布为二项分布的一个特例，只有一次实验
• 两者均只有两种可能的结果，即成功和失败

2. 泊松分布与二项分布
   泊松分布是二项分布的极限分布，条件如下：

• 试验次数足够多或者说$n\to \infty$
• 每次试验成功的概率相同，无穷小,
• $\lambda =np$，有限。

3. 正态分布和二项分布 & 正态分布和泊松分布
   正态分布是在以下条件下二项分布的另一种极限形式，条件如下：

• 试验次数无限大$n\to \infty$
• $p$和$q$都不是无限小的。

正态分布也是参数$n\to \infty$的泊松分布的一个极限情况。

CSDN: 数据科学家必知常见概率分布