由于自己最近在学习贝叶斯网络,在学习中遇到一些问题,查找相关资源的博客很少,自己就写了点学习笔记。
首先,介绍贝叶斯网络(Bayesian Network,简称BN)是一种特殊的图形模型,是有向无环图(Diected Acyclic Graph,简称DAG)。也就是说,在贝叶斯网络中,所有的边都是有方向的(即指向一个特殊的方向),而且不存在回路(即不存在这样的一条路径,从某个节点出发,沿着一组有向边前进又回到出发点)。下图是贝叶斯网络的一个简单的例子:
其中,节点集合为{A,B,C},边的集合为{BA,BC}。这组成了一个有向无环图:
1. 没有任何无向边(没有双向的边)。
2. 没有环路(从任何一个节点出发,经过有向边,无法回到出发节点)。
上图中,已知节点B的情况下,节点A和C相互独立,则P(A|B,C)=P(A|B)。根据此贝叶斯网络,可知所有变量的联合概率密度函数为:
P(A,B,C)=P(A|B)*P(B)*P(C|B)
对于通常的贝叶斯网络,已知节点X=X1,X2,...,Xn,根据链式准则(Chain Rule),其联合概率密度函数为:
其中,parant(Xi)是节点Xi的父节点(parant)的集合。
1 贝叶斯网的学习简介:
贝叶斯网的学习就是确定贝叶斯网的网络结构和与之相应的参数,在已知节点数目的条件下,贝叶斯网的结构和参数可以有3中方式确定:
1. 通过专家只是确定网络的结构,并指定它的分布参数。
2. 通过专家只是确定网络的结构,然后从数据中学习网络的参数。
3. 直接从数据中学习贝叶斯网的结构和参数。
贝叶斯定理:在贝叶斯解释下。事件的先验概率表示为,提供概率的主体所据有的知识。贝叶斯定理把事件的先验概率与后验概率联系起来,用来表示事件的后验概率:
当不知道p(x|ε)时,bayes做了如下假设:如果没有任何先验知识确定p(x|ε),则采用均匀分布作为其分布,这个称为贝叶斯假设。
贝叶斯网把贝叶斯理论应用于图中,在图中,如果从节点A有一条指向节点B的弧,则节点A叫做节点B的父节点,所有父节点组成父节点集,用∏i表示第i个节点的父节点集,给一个域U={x1,x2,…,xm},其中x1,x2,…,xm为m个离散变量,用这些变量表示网络的节点,因此,网络的节点也叫节点变量。在根据变量间的依赖关系用有向弧把节点连接起来,就构成域U的贝叶斯网,它就表示域中变量的联合概率分布。把节点进行排序,即每个节点都排在其父节点的后面,根据概率的链规则,节点变量的联合概率为:

根据变量间的独立性关系,对于每一个变量xi,存在一个子集∏i⊆{x1,x2,…,xm},使得xi和{x1,x2,…,xm}在给定∏i时条件独立,则:
2 贝叶斯网的学习:
贝叶斯网的学习就是确定贝叶斯网的网络结构和参数。当前比较流行的方法是从数据中学习贝叶斯网,数据指的是域U的一组观测值:D={x1,x2,…,xn},其中xi=(x1i,x2i,…,xmi)为一个观测实例,i=1,2,…,n,n为实例个数。根据观测状况数据可分为完备数据集和不完备数据集。完备数据集中的每个实例,都具有完整分观测数据,不完备数据集是指对某个实例的观察有部分缺值或者观测异常的情况。结合对贝叶斯网了解的先验知识,贝叶斯网的学习可分为4种情况:
1. 知道网络结构,数据完备
2. 知道网络结构,数据不完备
3. 不知道网络结构,数据完备
4. 不知道网络结构,数据不完备
3 贝叶斯网参数的学习:
贝叶斯网的参数学习就是在已知网络结构(从先前已知或者从数据中学习得到)的条件下,来确定每个节点的条件概率表。根据贝叶斯网节点变量的取值不同,将贝叶斯网分为离散型贝叶斯网,连续型贝叶斯网和混合型贝叶斯网。目前研究的最多的是离散贝叶斯网,对于含有连续变量的贝叶斯网,参数学习可分两大类:
1. 先对连续变量进行离散化,再用离散变量学习的学习方法
2. 通过设置一些约束条件,直接对其进行处理。
文献[2] 提出了一种叫做LCGBN(LinearConditional Gaussian Bayesian Net-works)的方法用于混合贝叶斯网的参数学习.LCGBN作了如下假设:①连续随机变量服从正态分布;②离散变量节点的父节点只能是离散的,连续变量节点的父节点可以是离散的或连续的.LCGBN作了如下假设:
1. 连续随机变量服从正态分布;
2. 离散变量节点的父节点只能是离散的,连续变量节点的父节点可以是离散的或连续的
对于不完备数据,先要用近似的方法,如Monte-Carlo方法、Gaussian逼近、EM算法和Gibs抽样法等对缺失数据进行估计.这些估计方法都是基于数据缺失是随机的假设,但在实际中,这一假设常常不成立,针对这一情况,文献[3]提出了一种叫做RBE(Robust Bayesian Estimator)的不基于这一假设的贝叶斯网的参数学习算法,它通过进行灵敏度分析来增强算法对数据缺失的健壮性.对完备数据D进行参数学习的目标是找到能以概率p(xi+θ)形式概括数据D的参数θ.寻找θ一般先指定一定的概率分布,如β分布、多项分布、正态分布、泊松分布等,然后估计这些分布的参数.
对完备数据,有2种常用的贝叶斯网的参数学习算法:最大似然估计法和贝叶斯方法.这2种方法都是基于独立同分布(IndependentIdentifyDistribution)假设的:
1. 样本数据是完备的;
2. 各实例之间是相互独立的;
3. 各实例服从统一的概率分布.
4 贝叶斯网的结构学习
贝叶斯网的结构学习的目的就是在给定数据D的条件下,找到一个与D最匹配的有向无环图。
以后会在深入学习每个阶段,学习中,希望一起讨论。
文章参考文献可以参考《贝叶斯网的学习与应用研究综述》论文。









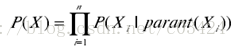
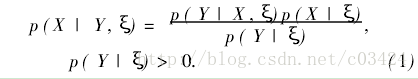
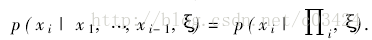

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








