现代密码学（四） 哈希函数和应用

定义

1. Hash函数简单定义：接受一定长度的输入并压缩成短而固定长度的输出的函数
2. 好的Hash函数:有较弱的碰撞性(碰撞是一定存在的，因为长度缩短)
3. 碰撞性：指有一对不同的输入量a和a’满足H(a)= H(a’);这种情况也称作a和a’在H下发生碰撞。
4. Hash函数：当且仅当输入参数x的长度l’(n)>l(n)时，就称(Gen,H)是输入长度为U(n)的定长散列函数。
5. 要求低碰撞函数，有两个地方与之前我们使用的key不同
   1. 不是所有的字符串都需要对应有效的密钥（即H^s®可能对某些s没有定义)。因此密钥s由Gen算法产生，而不是均匀随机选取的。
   2. 密钥s并不是保密的 。 它只是用在一个特定的函数H^S中,所以将它放在函数右上方
      
6. 碰撞发现实验7. 散列函数安全性有三种不同的安全水平
   1. 抗碰撞：最强的安全定义
   2. 抗第二原像：如果给定输入s和r，对概率多项式时间的敌手来说，找到x≠x’满足H(x’)= H(x)是不可行的。
   3. 抗原像:如果给定输入s和y = H(x)(不是x本身)，对概率多项式时间的敌手来说，找到一个x’使得H(x’)= y是不可行的。（理解一下，就是H（x）时单向的）

域扩展：The Merkle-Damg˚ard Transform

The Merkle-Damg˚ard Transform是将压缩函数扩展到成熟的哈希函数的一种常见方法。它的意义在于当要构建一个抗碰撞的Hash函数时，我们可以先只考虑固定长度的输入

如何通过The Merkle-Damg˚ard Transform将固定长度的输入扩展成任意长度的输入：
图示：
定理：如果（Gen , h）是一个定长抗碰撞散列函数， 那么（Gen , H）是一个抗碰撞散列函数

证明：原理是将（Gen , H）的安全性规约到（Gen , h）的安全性，证明任何（Gen ,H）的碰撞导致了（Gen , h）的碰撞。假设x1和x2是两个不同的串，长度为l1和l2

使用Hash函数的消息认证

将输入l（n）扩展到任意长度也能保证安全性的构造方法：
if Π is a secure MAC for fixed-length messages and (Gen, H) is collision resistant
上面结果的两个因子中第一个碰撞概率可以忽略不计，第二个在不碰撞下新建一个新建一个消息正确对应的t可以忽略不计

HMAC

意义：构造一个直接使用Hash函数不需要使用块密码就能解决任意长度安全MAC算法
内部计算：之所以要将k纳入内部计算值，是因为HMAC使用的是抗第二原像，

外部计算：

其中y^表示内部计算后，加上计算后长度的填充到分组长度，假设这是一个安全的固定长度MAC，那么HMAC可以看做hash-and-mac的实例化

图示：

生日攻击

假设给定一个散列函数H:{0,1}*→{0.1}”。(为了简单起见，假定散列函数的输入为任意长度，尽管攻击略微改动后对定长散列函数也适用。既然攻击独立于任何密钥，在这里省略密钥s.）攻击照下面的方式进行:任意选择q个不同的输入x1,…,xq∈{0,1}^2l，计算yi:=H,，并检查是否有两个yi相等。

1. 如果q>2^l，该事件的概率为1
2. 当q=0(2^l/2)时，这种碰撞的概率大约是1/2。在生日攻击的案例中对于365天，如果有23个人在房子里，那么两个人生日相同的概率就大于1/2。
3. 缺陷是需要大量存储空间来存储结果，比如生日攻击中需要365，如果对于长度为128的密钥来说就最多需要2^128这么多存储空间来存储键值对

小存储空间的生日攻击

在每一步中，对x和x’进行比较;如果相等，那么H(x)和H(H(x’))是一个碰撞（除非刚好相等，但是如果定义H是随机函数，这个事件发生的概率可忽略)。关键问题是这里需要的存储仅仅是存储x和x’。

Time/Space Tradeoffs for Inverting Functions

翻转算法即给了y=H(x)，目标是找到x’满足H(x’)=y

1. 对于{0,1}^l →{0,1}^ l的H，找到反转最简单的方法是记录下每一个｛x，H（x）｝,这需要存储O(2^l)个点，并使用O(2 ^l)这么多时间
2. 如果H定义了一个循环，即x，H(x),H(H(x))，代表了以x为起点的所有情况，N=2^l,记
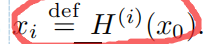
   然后将整个环划分成√N段，每段长√N，存储的时候只需要存储每段的开始点和结束点的键值对，即：
   那么当攻击者想要找到y的反转函数，只需要计算H(y),H(H(y)),看这些值有没有对应哪一个后端点，因为y是在整个环中的一部分，所以在最多√N次尝试下就可以找到一个后端点使得H^k(y)=x<i+1>.√N>。找到了这个后端点后，根据键值对，可以找到相应的前端点，那么在做√N-k次H运算，就可以找到y的反转函数了。

this attack stores O(√N) points and finds preimages with probability 1 using O(√N) hash computations.

Hellman’s time/space tradeoff

同前面所讲，Hellman的时空权衡也是存储起始点和终点。其中起点统一从
里选取，每个起点对应的终点通过t重迭代H函数得到

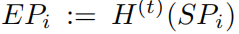
所以当收到一个y准备找其反转时，有两种情况：

1. 成功：y，H(y),…H^(t-1)(y)等于上述其中之一的端点（最先匹配），便可以直接通过序号进行计算
2. 失败：
   1. y不在生成表的初始过程中获得的s·t值（不计算起点）的集合中，并且就算将s*t的值设置的很大，甚至大过了N，也不能保证一定会有y，因为超过N^1/2后，碰撞会经常发生
   2. 尽管匹配了一个端点，但是计算的第二原像结果不是y，这是因为有可能存在碰撞，导致不是y的计算值被先匹配了（这被称为假阳性false positives）当然在一个抗碰撞的序列里，概率可忽略不计

随机预言机模型

只是一个将二进制字符串作为输入，并返回一个二进制字符串作为输出。盒子的内部工作是未知的，难以理解，并且任何人都可以使用，且相同的查询会返回相同的结果。没有人“知道”整个函数H，充其量，所有已知的是迄今为止已明确查询的字符串上的H值。

• 有两种方法可以让H有统一的选择

  1. 一次性完成映射
  2. 查询x时，它首先检查表中的某些对(xi，yi)是否有x=xi；如果是，则返回相应的值yi。否则，选择统一字符串y∈{0,1}`

• 随机预言机的三个特性：

  1. 如果x尚未被查询到H，则H(x)的值是一致的
  2. 如果查询x到H，还原可以看到此查询并学习x
  3. 还原可以将H(x)的值（即对查询x的响应）设置为其选择的值，只要该值正确分布，即均匀分布。

• 若Lin<Lout,随机预言机可以用作伪随机生成器，但他不是，因为参数不是固定的

• 若Lout<Lin,随机预言机可以作为抗碰撞哈希函数

• 用随机预言机构造一个为随机函数

• 反对使用随机预言机的原因：随机预言机模型使用H函数不能达到真正的随机，因为在现实世界中H在使用时一定是被固定了的

• 支持：在随机预言机模型下的安全性证 明 比起没有任何证明要好得多 。（即先完美证明，在考虑伪随机替换随机）

Hash的一些其他应用

Fingerprinting and Deduplication

1. Virus fingerprinting：存储一个包含已知病毒Hash的数据库

2. Deduplication:重复数据消除可以通过首先让用户上传他们要存储的新文件的Hash来实现；如果具有此哈希的文件已经存储在云中，则云存储提供商可以简单地添加一个指向现有文件的指针

3. Peer-to-peer (P2P) file sharing:服务器中将存储文件的Hash和唯一标识符，真正传输时再从源文件提供方进行传输

4. Merkle Trees:当上传多个文件存储时，可以使用O(logt)的时间来验证t个输入，这是一种折中的方法
   当需要验证某个文件时，只需要计算该文件和根节点之间的值，最后得到这次计算的根节点值，与之前根节点值做对比，如果H是抗碰撞的，则服务器不可能发送将导致验证成功的错误文件
   

5. 密码：将密码对应的Hash值存储到数据库，当用户输入密码时做Hash然后再比较，但用户的密码通常有规律（选择域），容易被暴力破解，有两种方法可以缓解这种攻击：

   1. 多次Hash
   2. 加盐hpw=H（s、pw）

6. 密钥导出：若将Hash看作是随机预言机，便可简单从高最小熵中导出随机均匀的密钥

   1. 最小熵

7. 承诺系统：允许一方通过发送承诺值com来“承诺”信息m，它有两个特点：

   1. com不显示m的任何信息
   2. com唯一标记一个m

   通常情况下，首先由Gen生成params，COM收到params和m并输出结果com=COM（params,m,r）,r为随机数。发送方选择一个r，计算后将com发送给接收方。发送方之后可以发送m和r给接收方来承诺（揭示）m