更多算法详解见:gitee
回文串定义:即正着看反着看都一样的字符串,如 a b a 、 a a a 、 c a c aba、aaa、cac aba、aaa、cac,回文串可以分为奇回文串和偶回文串, a b b a abba abba就是一个偶回文串, a b a aba aba就是一个奇回文串
求最长回文串的其他思路
求最长回文子串的方法,最容易想到的就是暴力枚举,将所有的回文子串都找出来,然后找做大的,时间复杂度就相当高了 O ( n 3 ) O(n^3) O(n3)。
还有比较容易想到的就是区间 d p dp dp,想法就是 S [ i ] S[i] S[i]到 S [ j ] S[j] S[j]是回文串的前提是 S [ i + 1 ] S[i+1] S[i+1]到 s [ j − 1 ] s[j-1] s[j−1]是回文串,是区间 d p dp dp时间复杂度就是 O ( n 2 ) O(n^2) O(n2),对于暴力枚举来说有所优化。
还有另一种枚举的方法,是中心扩散法,利用了回文串的对称性,枚举每一个字符,然后从中心向两边比较,时间复杂度也为 O ( n 2 ) O(n^2) O(n2)
今天介绍的这个算法可以将时间复杂度降到线性的 O ( n ) O(n) O(n)。
算法思路
马拉车算法充分利用了回文串的对称性和之前遍历过的区间。算法的主要思路是维护一个最右回文子串,利用该区间的对称性,计算当前遍历位置为中心的回文半径,回文半径就是从中心(如果为奇回文串,就包含中心位置)到回文串一端的距离。
我们设有字符串 S S S, S [ l … r ] S[l\dots r] S[l…r]为串 S S S中区间为 [ l , r ] [l,r] [l,r]的子串, S [ i ] S[i] S[i]表示串 S S S中第 i i i个字符,我们用 d [ i ] d[i] d[i]表示以第 i i i个字符为中心的回文半径。为了便于理解我们这里先只考虑奇回文串。
我们现在维护一个最右回文子串 S [ l … r ] S[l\dots r] S[l…r],设该回文串的中心是 S [ m i d ] S[mid] S[mid],设这个回文子串的回文半径为 d [ m i d ] d[mid] d[mid]。那么我们要求的当前位置的回文半径 d [ i ] d[i] d[i]就要有下的几种情况
i i i在 [ l , r ] [l,r] [l,r]的范围内
我们假设 j j j为 i i i关于 m i d mid mid的对称点,对应 j j j又有三种情况
- 以
j
j
j为中心的回文子串在
[
l
,
r
]
[l,r]
[l,r]内
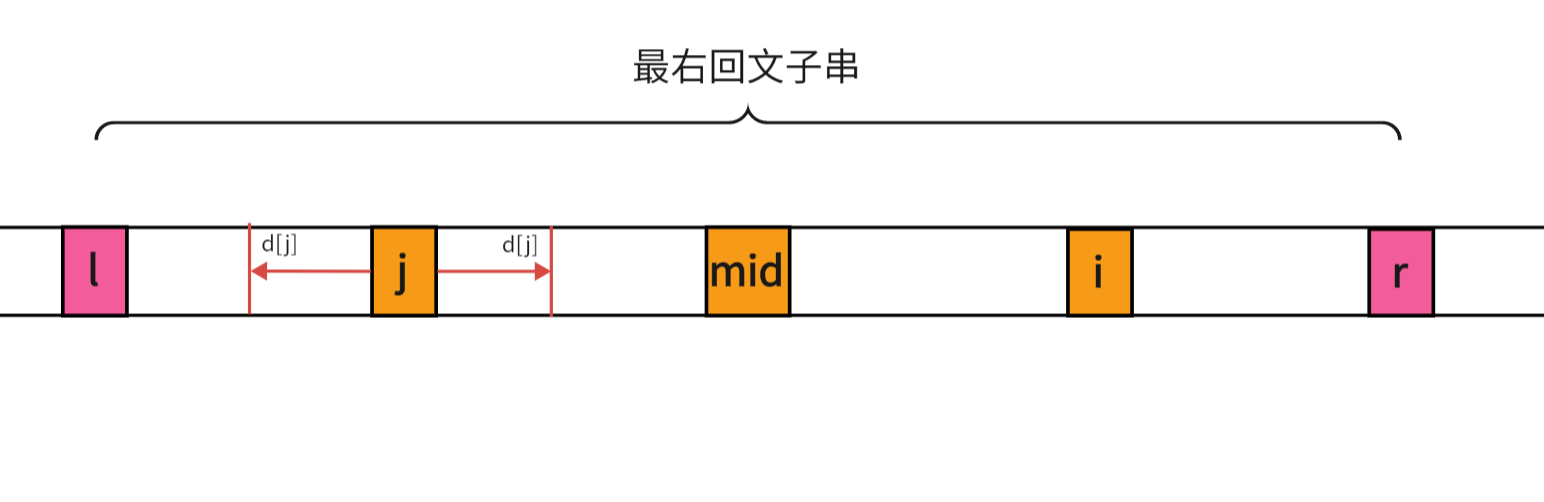
根据回文串的对称性,我们很容易就可以知道 d [ i ] = d [ j ] d[i]=d[j] d[i]=d[j] - 以
j
j
j为中心回文子串有部分在最右回文子串的外面
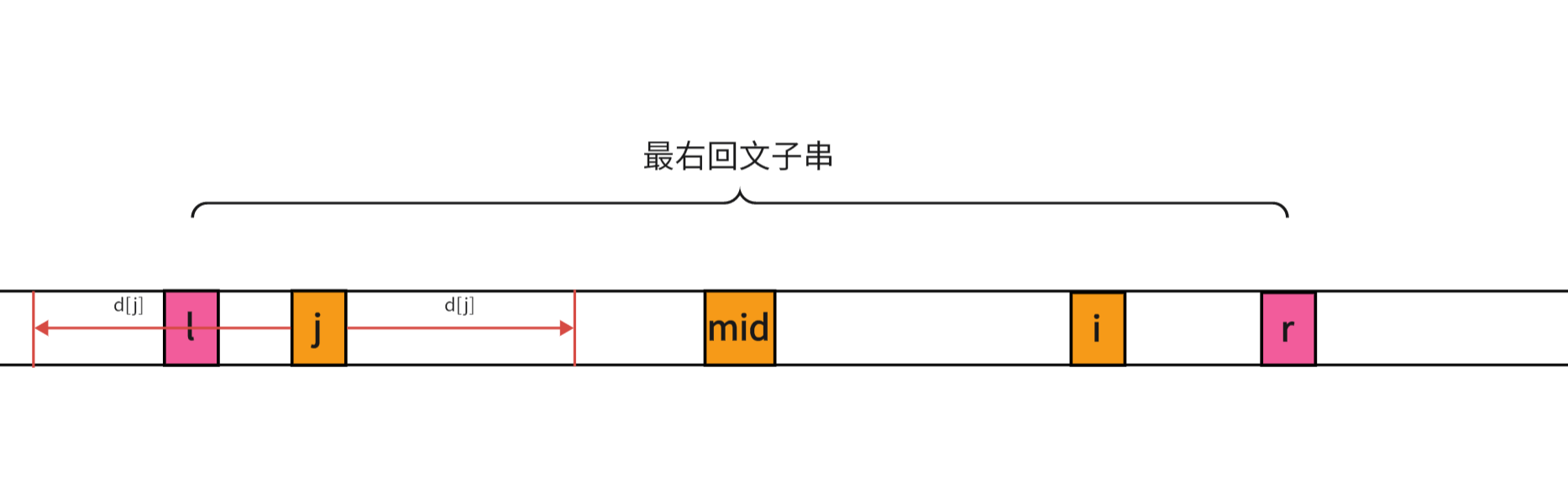
显而易见的, j − l = r − i = c j-l=r-i=c j−l=r−i=c, [ j − c , j + c ] [j-c,j+c] [j−c,j+c] 可以由 m i d mid mid对称到 i i i,所以 [ i − c , i + c ] [i-c,i+c] [i−c,i+c]是回文子串,那么以 i i i为中心的回文半径还可以继续增加吗?答案是不行,假如我们让 i i i的回文半径再增加 1 1 1
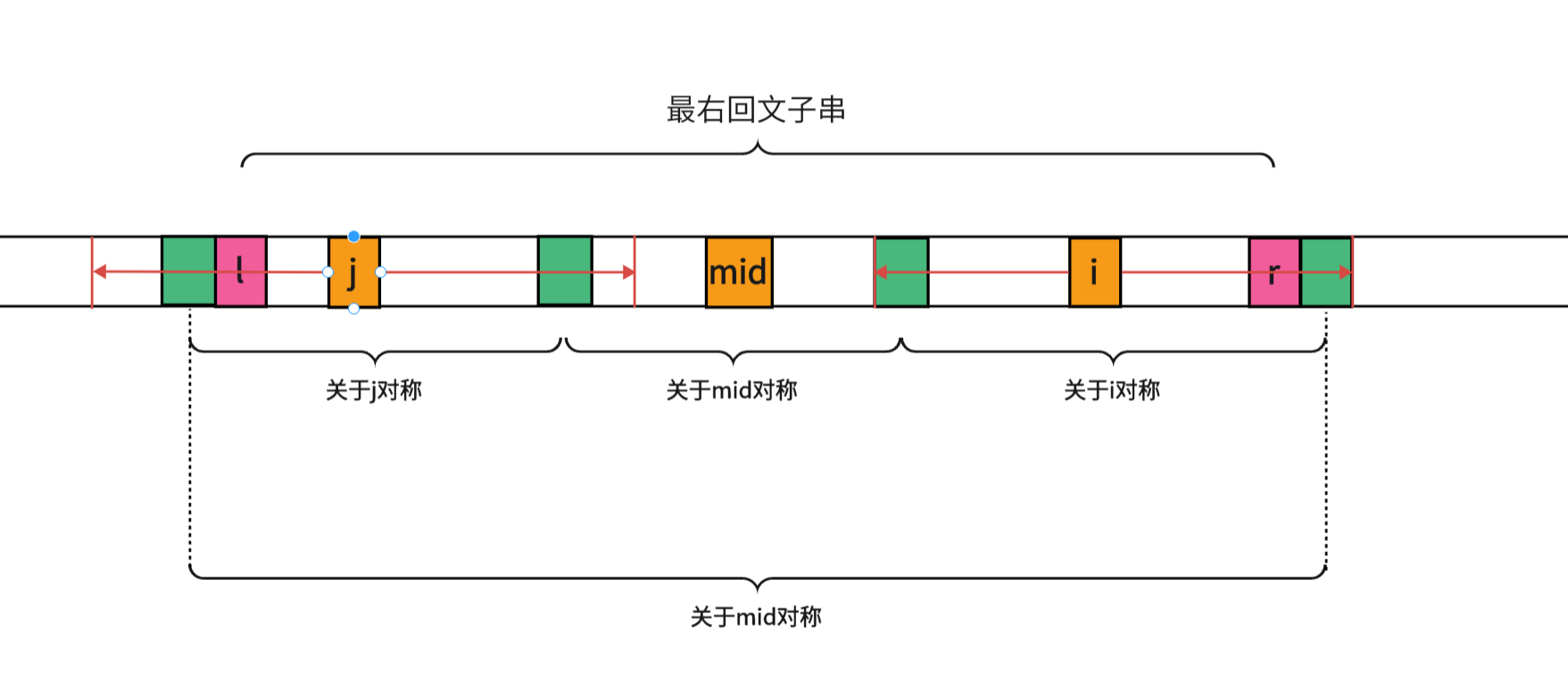
图中绿色的方块都是通过对称性得到的相等的字符,但是最右和最左的两个绿色方块一定是不相等的,因为如果相等 d [ m i d ] d[mid] d[mid]也会增加,从而使得最右回文子串包含他们,但是这里并没有包含,所以最左和最右的两个字符一定不相等,与对称性得到的结论相悖,所以以 i i i为中心的回文半径就是 r − i + 1 r-i+1 r−i+1 - 以
j
j
j为中心的回文子串的左边界和最右回文子串重合
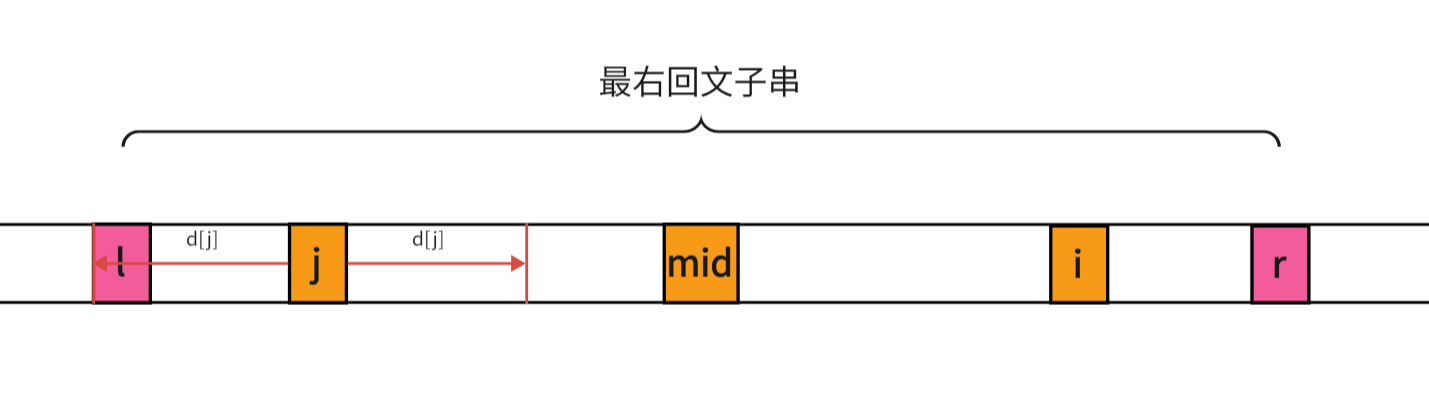
这种情况我也可以很容易的看出 d [ i ] ≥ d [ j ] d[i]\ge d[j] d[i]≥d[j]的,这时 d [ i ] d[i] d[i]是可以继续增加的,所以我们就要用中心扩散法来求得 d [ i ] d[i] d[i]
i i i在 [ l , r ] [l,r] [l,r]外
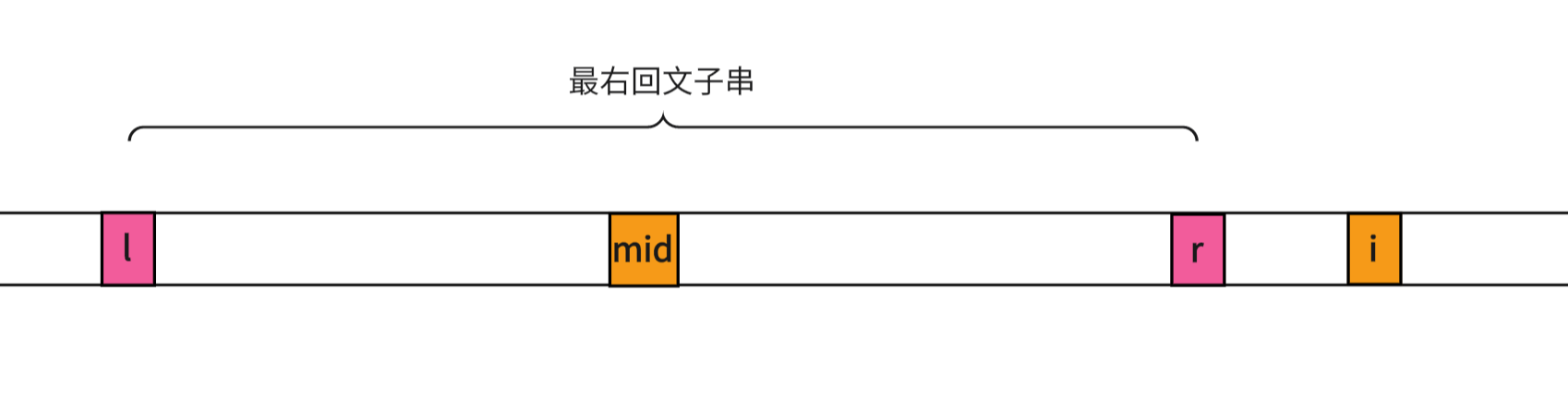
这时我们不能利用对称性来判断回文半径,就要用中心扩散法来求
d
[
i
]
d[i]
d[i]的值。
算法运行过程种,如果有比 [ l , r ] [l,r] [l,r]更靠右的回文子串区间,就要更新最右回文子串
根据上面的分析,我们很容易可以看出:
当
i
i
i在
[
l
,
r
]
[l,r]
[l,r]内时
d
[
i
]
=
m
i
n
(
d
[
j
]
,
r
−
i
+
1
)
d[i]=min(d[j],r-i+1)
d[i]=min(d[j],r−i+1),但是当边界重合时,还是要中心扩散法求
d
[
i
]
d[i]
d[i]
当
i
i
i在
[
l
,
r
]
[l,r]
[l,r]外时要中心扩散法求
d
[
i
]
d[i]
d[i]
处理奇偶回文串
上面的方法只适用于判断奇回文串,因为偶回文串没有中心字符,就不适用了。我们可以再每个字符之间加入特殊字符,奇回文串的中心不变,偶回文串的中心就变成了特殊字符。
我们还可以在字符首尾加上两个不同的特殊字符,这样边界也不用考虑了。
e
g
:
a
b
c
b
a
⟶
@
#
a
#
b
#
c
#
b
#
a
#
!
eg:abcba \longrightarrow @\#a\#b\#c\#b\#a\#!
eg:abcba⟶@#a#b#c#b#a#!
C o d e Code Code
实现时我们用 m i d mid mid最右回文子串的中心和 r r r最右回文子串的右端点,来维护最右回文子串区间
int Manacher(string& s) {
vector<int> d(s.size() * 2 + 3);
//初始化字符串
string str("@");
for (char ch : s)
str += "#",str+=ch;
str += "#$";
//我们用mid,r来维护最右回文子串
//len是最长回文子串的长度
int r = 0, n = str.size(), len = 0, mid = 0;
for (int i = 1; i < n - 1; ++i) {
//判断i是否在最右回文区间内
if (i <= r)d[i] = min(d[(mid << 1) - i], r - i + 1);
else d[i] = 1;
//中心扩散法求d[i]
//这样写是为了追求代码简洁,因为其他情况并不会进入循环,不影响时间复杂度
//就不写额外的判断来区分情况了
while (str[i + d[i]] == str[i - d[i]])++d[i];
//更新最右回文子串
if (i + d[i] - 1 > r)mid = i, r = i + d[i] - 1;
//更新最长回文子串的长度
len = max(len, d[i] - 1);
}
return len;
}























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










