傅里叶思想漫谈：从希尔伯特空间到不确定性原理

©PaperWeekly 原创 · 作者｜Maple小七

学校｜北京邮电大学硕士生

研究方向｜自然语言处理

绪言

傅里叶分析理论是数学史上最为辉煌的成就之一，由此发展和延伸出来的一系列理论在大量学科领域有着深刻的应用，让一代代科学家家为之倾倒与奋斗。因此，傅里叶级数展开式是大学本科数学基础课的重点内容之一，也是广大理工科学生最难以理解的公式之一。 

傅里叶级数往往会首先出现在本科一年级数学分析的教材中，可惜的是，大多数教材都太过严肃，它们往往从无穷多个简谐振动的叠加原理引出三角函数系的概念，然后直接对傅里叶级数下定义，而没有深入探讨这里面蕴藏的思想。

有了定义之后，教材就会直接给出周期延拓与收敛定理，并抛出一堆练习题，似乎只是为了把公式印在学生的脑子里。面对这样突兀奇怪的公式，大多数人只能死记硬背，且仅仅满足于能套公式做题，完全忽略了傅里叶级数背后的美感与能够颠覆人们世界观的思维模式。

虽然笔者的本科专业是数学与应用数学，但直到大三学习随机过程的时候（平稳过程的谱分析）才真正接触到了傅里叶变换，遗憾的是，教材也仅仅让我们记住变换公式及其一些有用的性质，没有深入探讨其蕴含的思想，更没有将其与傅里叶级数对比。直到在泛函分析与数学物理方程的学习中，笔者才了解到了傅里叶级数与变换是如何与分析学和物理问题联系起来的，并渐渐领略到了傅里叶级数与变换及其一系列理论的精妙之处。

1.1 函数观念的变革

约瑟夫·傅里叶是法国著名数学家，物理学家，他的一生并不平坦，甚至富有一些传奇色彩。1807 年，傅里叶向巴黎科学院呈交了一篇关于热传导的论文《热的传播》，后被拉格朗日等人审阅后拒绝。傅里叶在 1811 年又提交了修改后的论文，修改后的论文虽获了奖，但仍被批评其论证不够严密。

傅里叶最后只能将自己的论文扩充成一本书，也就是他一生中最为辉煌的成就——《热的解析理论》。该书出版两年后，傅里叶被评为科学院的终身秘书，这是一个极有权力的职位，从而使得他的论文终于得以发表。

傅里叶在他的论文中大胆给出如下命题：

一个变量的任意函数，不论是否连续或不连续，都可展开为正弦函数的级数，而这正弦函数的参数为变量的倍数。

但是欧拉，拉格朗日等人认为解析的正弦函数无法表示非解析的函数，即使被表示的函数是解析的，也不一定会有周期性。 不仅是这两位数学家，18 世纪的大部分数学家都相信在特定区间上与正弦函数一致的函数也意味着在整个区间上与正弦函数是完全相同的，但实际上，这只是解析函数具有的性质，而欧拉等人将该性质错误地推广到了一切函数上。

傅里叶是第一个指出当一个函数在自变量的一个给定区间上确定时，在这个区间以外函数不能确定的数学家。他意识到只能在一段区间上而不是在整个定义域内用三角级数表示函数，超出这个特定区间展式不一定成立。除此之外，傅里叶还将奇函数与偶函数联系在一起，比如他曾将偶函数 展成如下多重弧的正弦级数：

傅里叶的做法遭到了很多数学家的反对，即奇函数和偶函数是不能互化的，但实际上，当考虑到公式的成立区间时，这种冲突就消失了。

虽然傅里叶的断言严格上说是错误的，傅里叶本人也没有给出证明（实际上，傅里叶级数收敛性的充分必要条件至今没有人能够给出），但这一断言里蕴藏的思想是极富有价值的，其直接改变了数学家对函数的概念，将人们从解析函数与可展成泰勒级数的函数中解放出来，引发了数学家对不连续函数的探讨，使得泛函分析与调和分析等领域得以诞生。

三角级数收敛性问题更是刺激了集合论的建立，直接影响了 19 世纪的数学研究方向。直到现在，傅里叶分析也是现代分析数学的核心领域之一，其辉煌的成就让一代代分析学家为之倾倒与奋斗。

当然，傅里叶一生的成就不仅仅只局限于热力学与微分方程，傅里叶在他的论文中还提出了量纲齐次原理，他对方程论有很广泛的研究，并在线性规划和力学上也有研究，他也是最早使用定积分符号 的人，他甚至是温室效应的发现者。这一系列成就也使得傅里叶在数学史上能与拉普拉斯，勒让德等人齐名。接下来，我们将深入讨论傅里叶级数、傅里叶分析理论方法的思想与应用。

漫谈傅里叶级数

傅里叶级数的导出不乏很多精妙的方法，傅里叶级数本身起源于傅里叶在解下面的热传导方程时遇到的问题：

2.1 内积空间中的傅里叶级数

空间是数学中最为重要的概念之一，当一个集合被定义了运算，就形成了空间。当我们定义了空间内元素的加法与乘法运算，并使其满足八条特定规则，空间就有了线性的结构。除此之外，我们还希望空间能有长度，角度等概念。

当我们定义了满足平移不变性和齐次性的长度概念后（若不满足，则只能称其为度量空间），线性空间就有了距离的结构，即赋范线性空间或 Banach 空间（不妨默认我们讨论的距离空间均是完备的），当我们进一步定义了角度，就得到了内积空间或 Hilbert 空间，这时候，我们就有了正交与投影等概念。

Euclidean 空间可以说是最简单的 Hilbert 空间，在二维和三维 Euclidean 空间中，长度（Norm），距离（Distance），垂直（Orthogonality）这些几何概念都是很直观的。然而，我们当然不能仅仅满足于在几何直观上讨论这些概念，我们完全可以将其抽象到 上面去。类似地，我们定义了向量的点积（内积）之后，也就是：

我们便可以讨论向量的长度（或范数）：

向量之间的距离：

与向量之间的垂直（或正交）

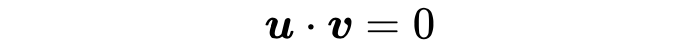
的概念了。不仅如此，向量空间的正交系，正交投影，正交分解这一系列概念都变得更加丰富了起来。

当然，在数学家眼中，向量和数字的概念一样，都是抽象的，并不依赖于其表达的实际含义。 中向量的元素是可数的，当我们把一个向量中的元素数量扩展到无穷的时候，向量就变成了函数。我们同样可以仿照之前给出的定义，对函数空间定义范数、内积、正交。

以区间 上所有连续函数（函数应满足平方可积的条件，即应属于 勒贝格空间）构成的向量空间 为例，仿照 内积的定义，将求和化为积分，则连续函数的内积定义为：

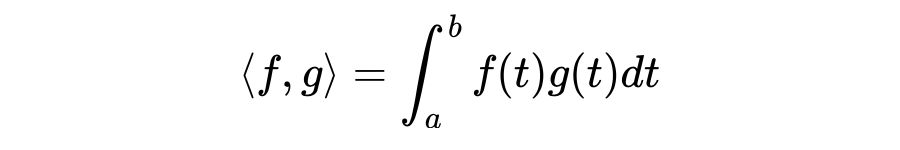
这个时候，我们便可以自然地定义两个函数的正交：

同样，我们对函数空间也有了正交基的概念，即可以考虑函数的正交分解。因为对任何 ，三角函数系：

关于如下的内积是正交的：

易见由三角函数系生成的空间 是 中的子空间，我们考虑 上的函数 ， 中用函数对 的最佳逼近称为 在 上的 阶傅里叶逼近，由于三角函数系正交，因此给出的最佳逼近是