重温状态空间模型SSM：有理生成函数的新视角

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 科学空间

研究方向 | NLP、神经网络

在前三篇文章中，我们较为详细地讨论了 HiPPO 和 S4 的大部分数学细节。那么，对于接下来的第四篇文章，大家预期我们会讨论什么工作呢？S5、Mamba 乃至 Mamba2？都不是。

本系列文章主要关心 SSM 的数学基础，旨在了解 SSM 的同时也补充自己的数学能力。而在上一篇文章我们简单提过 S5 和 Mamba，S5 是 S4 的简化版，相比 S4 基本上没有引入新的数学技巧，而 Mamba 系列虽然表现优异，但它已经将 A 简化为对角矩阵，所用到的数学技巧就更少了，它更多的是体现了工程方面的能力。

这篇文章我们来学习一篇暂时还声名不显的新工作《State-Free Inference of State-Space Models: The Transfer Function Approach》[1]（简称 RFT），它提出了一个新方案，将 SSM 的训练、推理乃至参数化，都彻底转到了生成函数空间中，为 SSM 的理解和应用开辟了新的视角

基础回顾

首先我们简单回顾一下上一篇文章关于 S4 的探讨结果。S4 基于如下线性 RNN

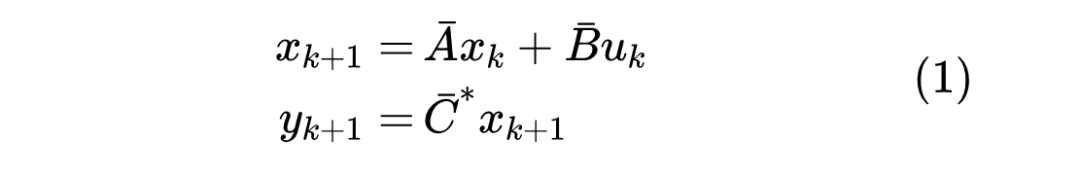
其中 ，这里旨在做一般化的讨论，所以我们绕过了 与 的联系，假设 为一般矩阵。设初始状态为零，那么直接迭代可以写出：

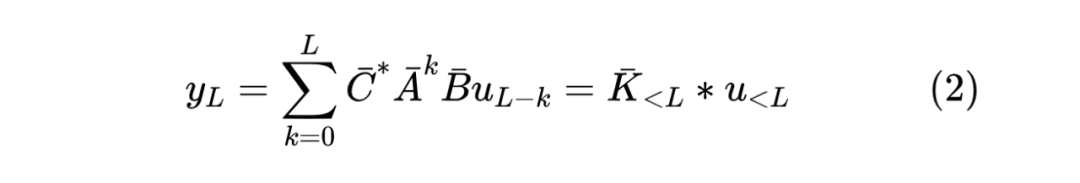
其中 是卷积运算，而

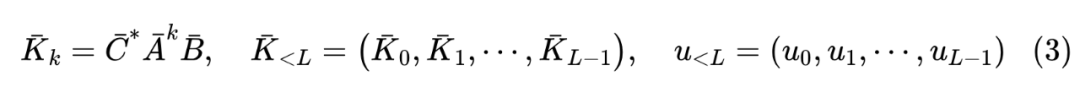
由于卷积可以通过离散傅里叶变换（DFT）高效计算，所以剩下的问题是如何高效地将 算出来，这就是 S4 的核心贡献。为此，S4 引入了生成函数

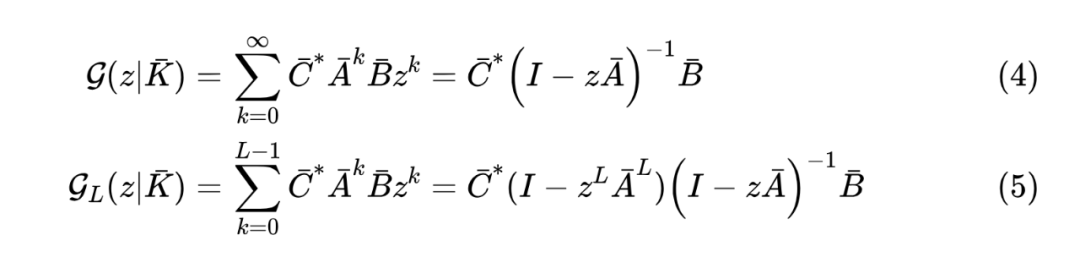
如果能够高效地计算 ，那么就可以代入 ，其结果就是 的 DFT，于是进一步逆变换（IDFT）后就可以得到 ，由于此时的 总满足 ，所以我们也可以设 ，那么 的形式就跟 一致了：

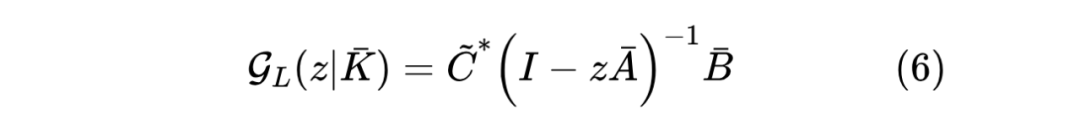
那怎么高效计算 或者 呢？S4 将 分解为“对角+低秩”的形式，然后通过 Woodbury 恒等式进行计算，其最终结果为

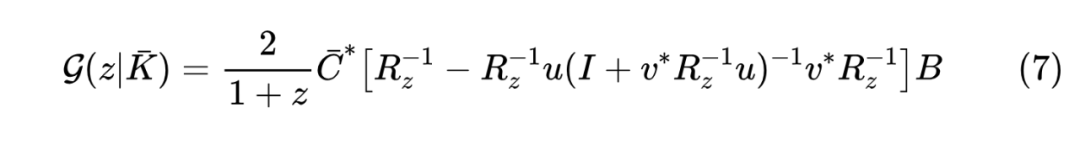
其中 是 的对角阵， 都是 的列向量，这意味着给定 计算 的复杂度为 ，而如果要对 进行计算，那么朴素实现的计算量是 。S4 提出可以将其转化为 Cauchy 核问题进行计算，复杂度进一步降低到 。

不管哪一种，我们可以发现其复杂度不仅依赖于 ，还依赖于 （state size），而 RFT 则提出了一种新方法，将复杂度直接降低到了最理想的 ，不依赖 state size，而且推导过程相比 S4 还明显简化，同时也不依赖于 是对角阵或者“对角+低秩”的假设。

有理函数

RFT 是 Rational Transfer Function 的缩写，它的重点是 Rational Function，即我们所说的有理函数（两个多项式相除）。它跟生成函数有什么关系呢？RFT 的作者们非常高明地观察到， 实际上是一个有理函数！具体来说，我们有

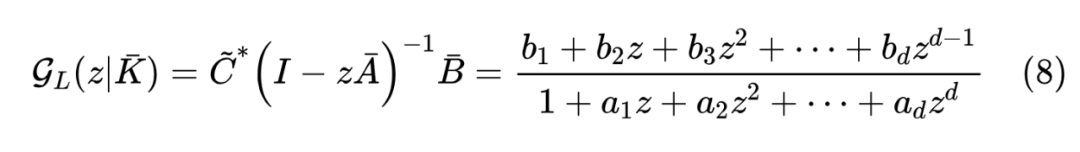
其中 都是标量，如果   都是实矩阵，那么它们都是实数。如果单纯想要意识到存在这么个相等的形式，我们只需要利用矩阵求逆的一个经典公式：

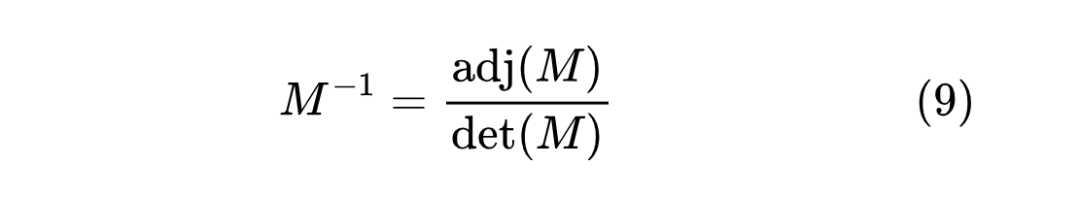
其中 是 的行列式，而 是 的伴随矩阵 [2]，由于伴随矩阵涉及到大量行列式计算，所以这个求逆公式在实际计算中通常没什么价值，但在理论分析时通常能起到奇效。比如，我们将它代入到 中，就得到

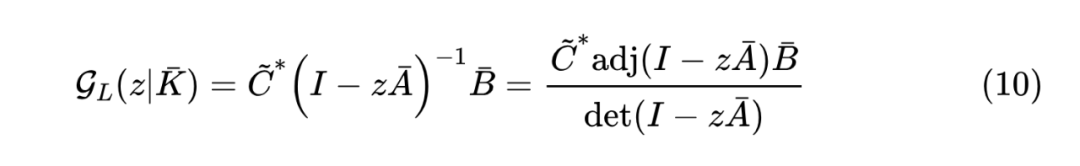
我们知道， 阶行列式多项 个元素相乘的求和，所以 是关于 的 次多项式；接着根据伴随矩阵的定义，它的每个元素都是 阶行列式，也就是 次多项式，左乘 和右乘 只不过是将这些元素加权求和，所以结果还是 次多项式。因此， 是 的 次行列式除以 的 次行列式，再将分母的常数项系数标准化为 1，就得到了式（8）。

对应关系

进一步，我们可以利用一个行列式恒等式来确定系数 与 的关系。这个恒等式是

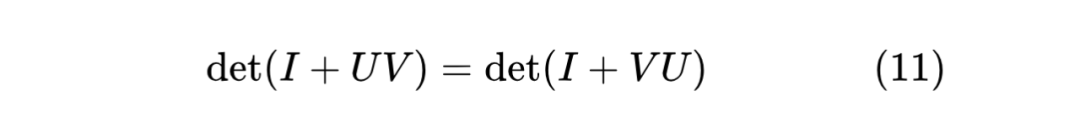
直接证明这个行列式不难，算是一道普通的考研题，只需要注意到

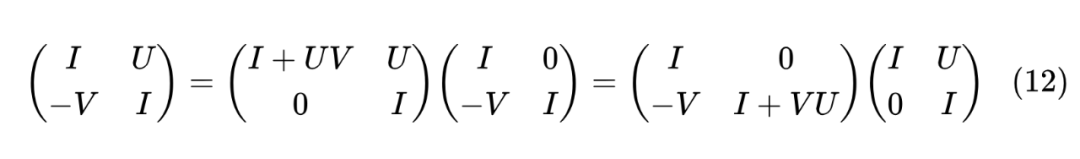
根据行列式的定义和形式，中间部份的行列式就是 ，最右边的行列式就是 ，它们同一个矩阵的行列式，所以结果相等。这个结果还可以进一步推广到（当 都可逆时）

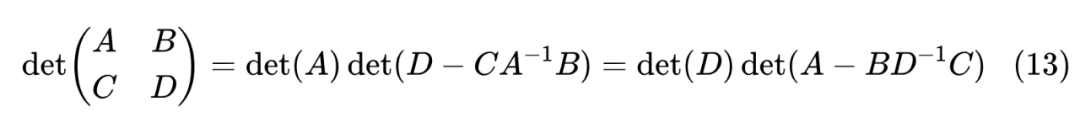
更远一点的话，它还可以一般化为我们在《两个多元正态分布的 KL 散度、巴氏距离和 W 距离》提过的“舒尔补（Schur complement）” [3] 理论。

回到正题，注意在式（11）及其推导中，我们不需要假设 都是方阵，所以实际上式（11）对于非方阵也是成立的，只要单位阵 自动匹配 和 的大小就行。特别地，如果 分别是列、行向量，那么 就是一个标量，对应的 就是 1，其行列式就是自身，即 。利用这个特例，我们有

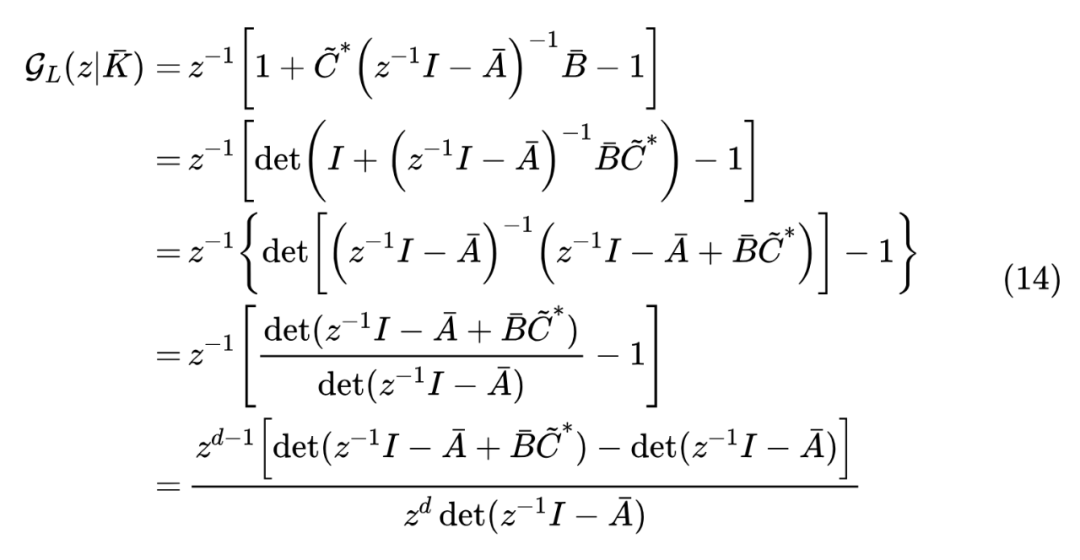
分母中的 ，是以 为变量的矩阵 的特征多项式，它是 的 次首一多项式，乘以 后变成了z的常数项为 1 的 次多项式；同理，分子中的 是 的特征多项式（ 的 次首一多项式），减去 后正好得到 的 次多项式，乘以 变成 的 次多项式。

所以， 向量正好是多项式 除最高次项外的各系数，而 b 向量则是多项式 的各系数（次数从高到低排序）。

惊喜突现

现在我们先缓一缓，思考一下我们做了什么，要往哪里去。

我们的出发点是线性系统（1），为了让它可以并行训练，我们将其转化为了 与 的卷积，就可以通过先 DFT 后相乘再 IDFT 来高效计算，因此这一步的效率不成问题。现在 是现成的，但 未知，所以问题变成了如何高效计算卷积核 ，为此我们进一步引入了生成函数 ，只要能够高效计算 ，那么就有

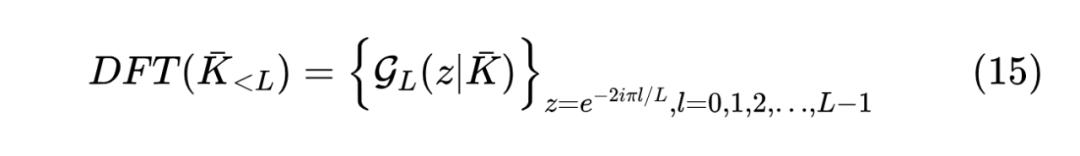
然后IDFT就可以恢复原本的 。对于 ，我们有 ，于是

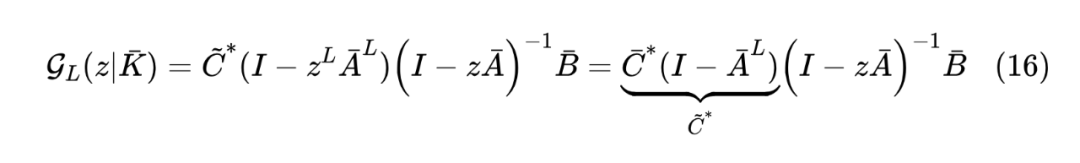
也就是我们可以先将整个 视为训练参数 ，事后再解出对应的 用于推理。

S4 通过“对角+低秩”的分解来计算 ，而这篇文章则指出 实际上是一个有理函数，即式（8）。如果我们此时代入 ，就会发现一些让人惊喜的结果，比如分母

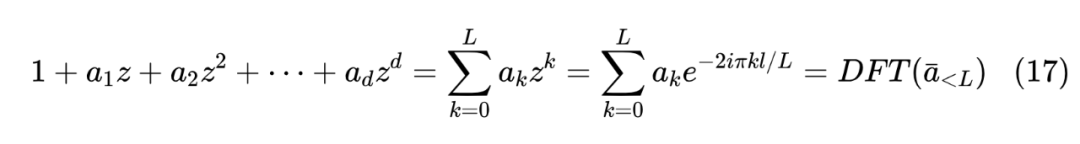
其中 ，也就是说，根据定义分母就是将 左边拼一个 1、后边拼若干个 0、凑成 个数后的 DFT！同理，定义 ，那么分子就是 DFT()，于是我们可以简单地写出

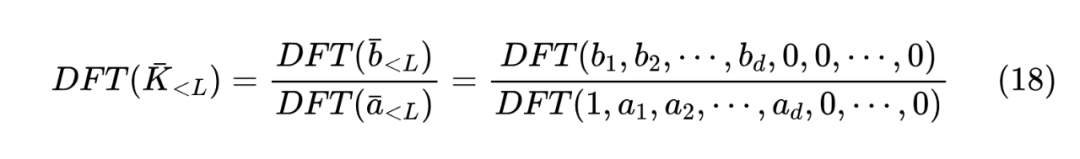
然后 IDFT 就可以得到 ，其中 DFT 和 IDFT 的计算复杂度都是 ，跟 无关（只需要 ）！这就是 RTF 的复杂度与 state size 大小 d 无关的核心思想。

另起炉灶

按照上面的引入顺序，我们的计算过程应该是先给定 ，然后计算 和 的特征多项式系数，进而得到 和 ，最后计算 DFT、相除然后 IDFT 来得到 。如果是单纯的计算，那么这个过程没啥问题，但我们面对的是训练场景， 可能带有训练参数，这时候计算 和 的特征多项式这一步就不那么容易传播梯度了。

对于这个问题，更加干脆的方案是“另起炉灶”——直接以 RTF 形式的式（8）为出发点，将 和 设为可训练参数，那么我们连特征多项式的计算都省了，直接就可以 DFT 和 IDFT 去算 。

不仅如此，原本 共有 个参数，现在 两个向量一共就 个参数，大大节省了参数量。而因为任意的 都可以算出对应的 ，所以 RFT 的理论能力是不差于原始的 RNN 形式的。

当然，RTF 只是提供了一种直接以 为参数的高效训练的方式，如果要做 step by step 推理，那么还是要转回 RNN 形式，这意味着给定训练好的 ，我们要找出一组 ，然后代入式（1）来推理。注意 是 个参数到 个参数的映射，肯定有无穷多组解，而我们只需要找出尽可能简单的一组解就行了。

友之矩阵

怎么求这组解呢？前面我们已经证明了， 向量正好是多项式 除最高次项外的各系数，所以给定 求 ，就是已知特征多项式的情况下求对应的矩阵，最简单的解是对角矩阵，假设 为 的 个根，那么让 即可。不过，这样可能会出现虚数根，某种程度上可能不够简洁，同时这种纯粹的形式解也无法直接观察 与 之间的联系。

事实上，求一个实矩阵使其特征多项式为给定的实系数多项式，这个问题早有研究，其答案有一个有趣的名字，叫做“友矩阵（Companion matrix）”[4]，其形式为（为了对齐原论文的结果，这里相比维基百科的格式多了个翻转）：

事后去证明该矩阵满足

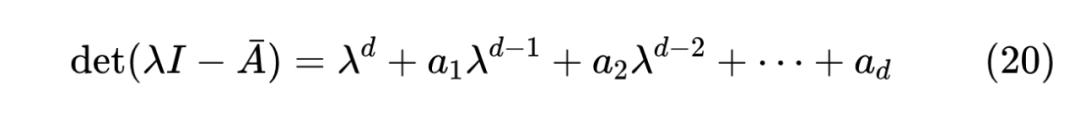
并不难，直接根据行列式的定义对 的第一行展开即可。更深刻的问题是如何想到这个构造，这里笔者提供自己的想法。根据特征多项式来构造矩阵，本质上就是逐渐将多项式变换为一个 只出现在对角线上的行列式，比如 时我们有

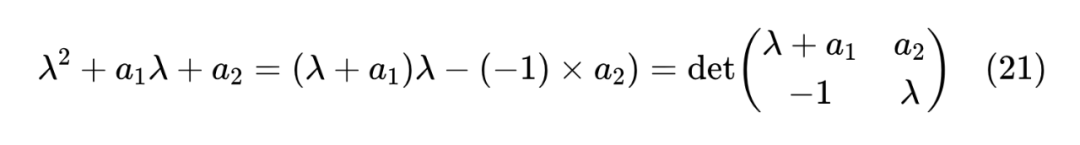
这就可以抽出对应的 。对于一般的 ，我们有

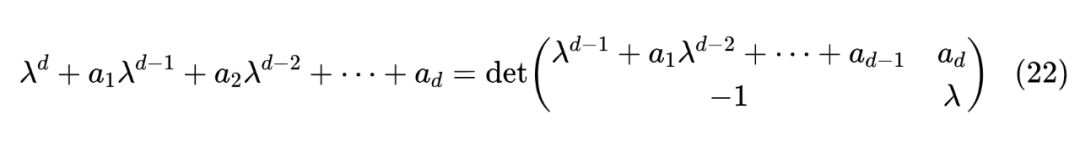
这当然还不是最终答案，但这成功将多项式的次数减少了一，这启示我们或许可以考虑递归地构建，即左上角再以 为特征多项式构造原矩阵，然后微调一下右上和左下的行列，形成分块矩阵。细心多尝试一下，就有机会自己构造出式（19）的结果。

有了 ，构造 就容易多了。还是根据前面的结论，我们有

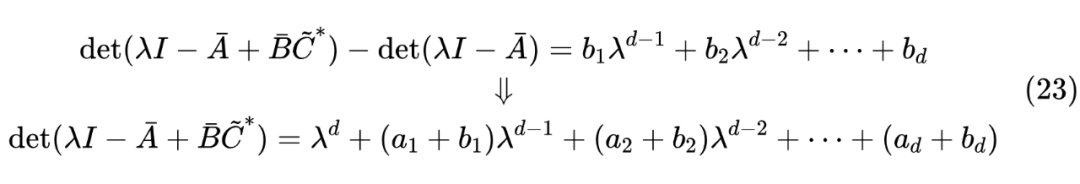
也就是 的特征多项式为上式，那么根据 的构造方式，我们得到 的一个解是

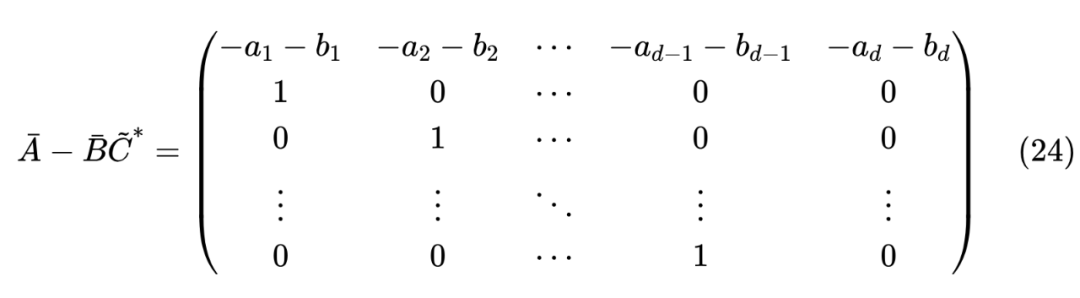
于是

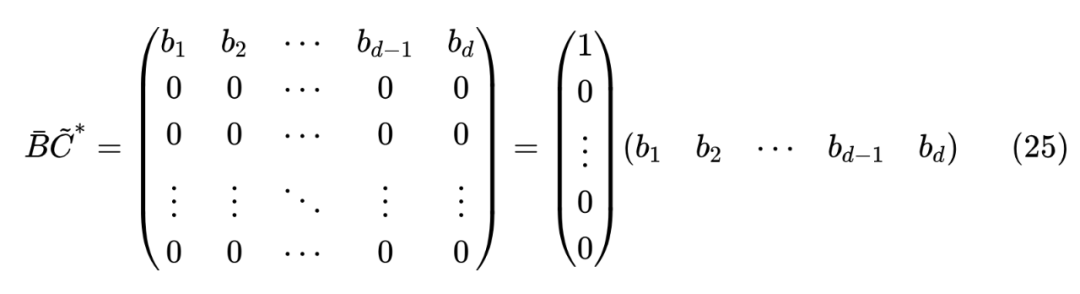
这意味着我们可以找到一组解 ，然后进一步解得 。

初始方式

我们来完整地 的递归形式：

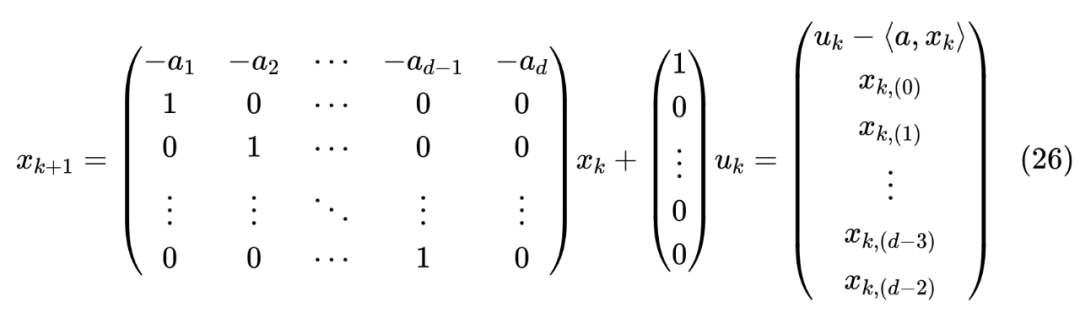
由于 极其稀疏的特点，每一步递归可以在 而不是 完成。特别地，当 时，我们可以得到：

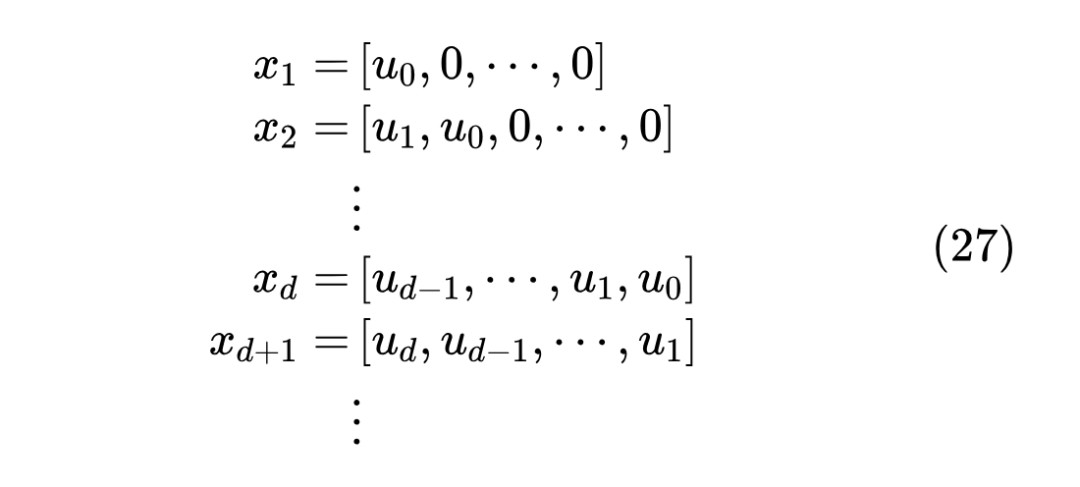
也就是说，模型一直在滚动储存最近的 个 ，如果没有任何其他先验知识，那么这很明显是一个很合理的初始解，所以原论文在初始化阶段将 设为零。

原论文对这个初始化还有一个增强数值稳定性、防止梯度爆炸的解释。从上一篇文章我们知道，线性系统（1）具备相似不变性，这意味着它的动力学跟将 对角化后的动力学在数学上是一致的，而 的对角化矩阵，就是它的特征多项式的所有零点组成的对角矩阵，如果某个零点 的模大于1，那么经过多步递归后就可能发生数值/梯度爆炸。

换句话说，我们最好可以约束 ，使得多项式 的所有零点的模都不大于 1，以获得更好的数值稳定性同时避免梯度爆炸。然而，保证多项式的零点都在单位圆内的充要条件依然不得而知，但有一个相对简单的充分条件是 。

结论：当 时，多项式 的所有零点模长都不超过 1。

证明：用反证法。假设该多项式有一个模大于1的零点 ，那么 ，于是

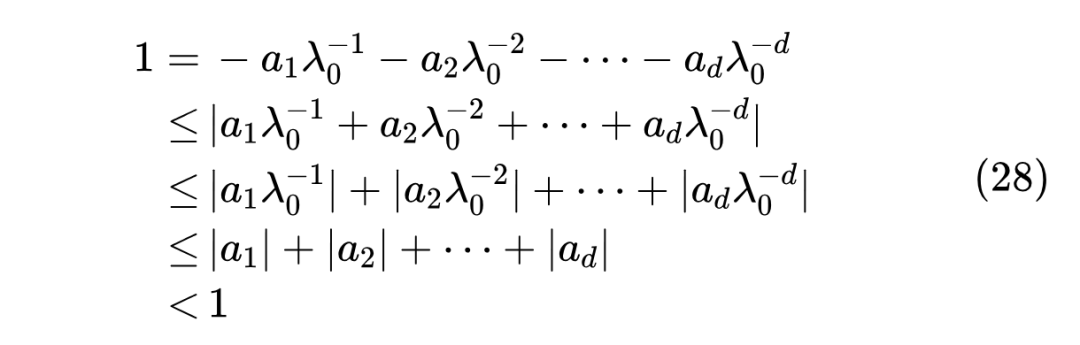
这就出现了 的矛盾，因此假设不成立，多项式的所有零点模长都不大于 1。

然而，RTF 指出，如果直接约束 满足 ，会大大削弱模型的表达能力，弊大于利；RTF 进一步发现，只需要在初始化阶段尽可能满足该条件，然后让模型自己慢慢学就行了。最满足这个条件的取值自然是 ，所以 RTF 选取了全零初始化。

实验效果

关于实验部份，下面两张图表就可以看出 RTF 的显著特点：

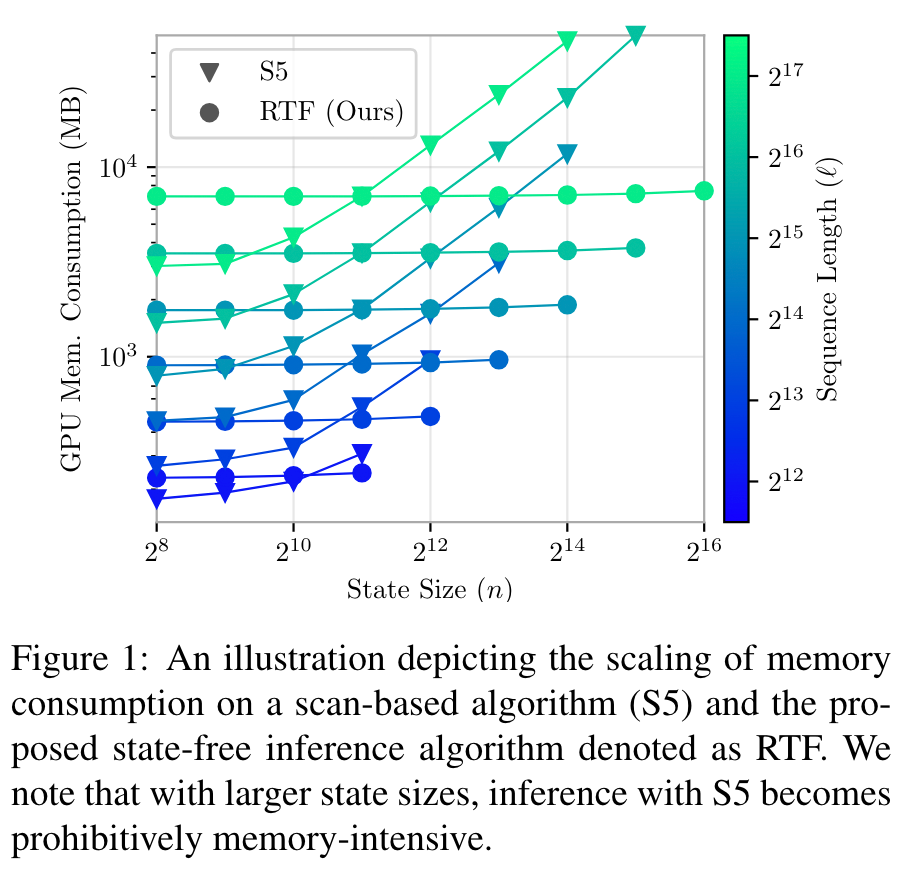
▲ RTF 的复杂度基本上跟 state size 无关

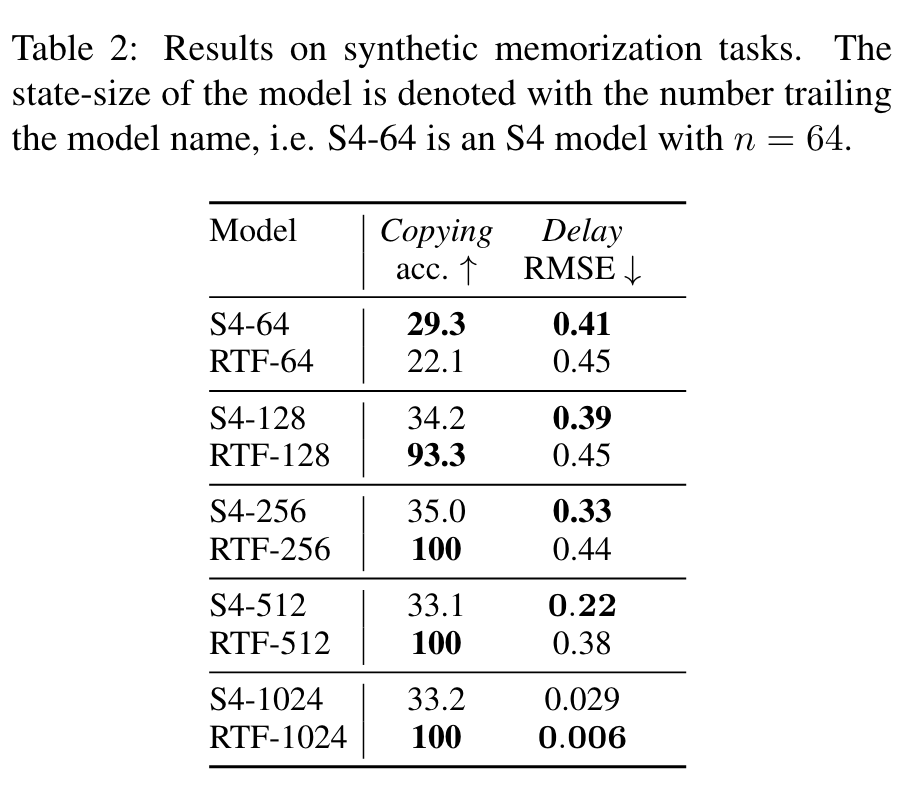
▲ RTF 可以通过增大 state size 来提高效果

第一张图显示了 RTF 的计算复杂度（时间、空间）跟 state size 没有明显关系，而正因为如此，我们可以通过增大 RTF 的 state size 来改善 RTF 的效果（反正不增加复杂度），也就是第二张图表所显示出来的效果。其他实验结果读者自行翻阅原论文即可。

文章小结

本文介绍了 SSM 模型的一个新工作 RTF，它观察到线性 RNN 的卷积核的生成函数实际上可以表示为一个有理函数（分式多项式），利用这个特点，我们可以将 SSM 的参数化全部转移到生成函数空间上去，并利用离散傅立叶变换来加速，这使得整个计算流程显著简化。跟 S4 的“对角+低秩”分解相比，RTF 也显得更为简明直观。

参考文献

[1] https://papers.cool/arxiv/2405.06147

[2] https://en.wikipedia.org/wiki/Adjugate_matrix

[3] https://en.wikipedia.org/wiki/Schur_complement

[4] https://en.wikipedia.org/wiki/Companion_matrix

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·

·

·