低秩近似之路：伪逆（Pseudo Inverse）

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 科学空间

研究方向 | NLP、神经网络

可能很多读者跟笔者一样，对矩阵的低秩近似有种熟悉而又陌生的感觉。熟悉是因为，低秩近似的概念和意义都不难理解，加之目前诸如 LoRA 等基于低秩近似的微调技术遍地开花，让低秩近似的概念在耳濡目染间就已经深入人心；然而，低秩近似所覆盖的内容非常广，在低秩近似相关的论文中时常能看到一些不熟悉但又让我们叹为观止的新技巧，这就导致了一种似懂非懂的陌生感。

因此，在这个系列文章中，笔者将试图系统梳理一下矩阵低秩近似相关的理论内容，以补全对低秩近似的了解。而在第一篇文章中，我们主要介绍低秩近似系列中相对简单的一个概念——伪逆。

优化视角

伪逆（Pseudo Inverse），也称“广义逆（Generalized Inverse）”，顾名思义就是“广义的逆矩阵”，它实际上是“逆矩阵”的概念对于不可逆矩阵的推广。

我们知道，对于矩阵方程 AB=M，如果 A 是方阵且可逆，那么直接得到 ，可如果 A 不可逆或者干脆不是方阵呢？这种情况下我们很可能找不到 B 满足 AB=M，这时候我们如果还想继续下去的话，通常是转为优化问题

其中 ，注意数域是 ，表明本系列文章关注的都是实矩阵，而 是矩阵的 F 范数（Frobenius Norm），用来衡量矩阵 AB - M 与全零矩阵的距离，其定义为

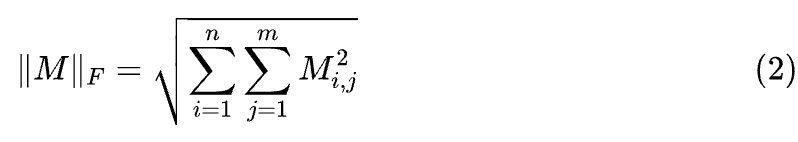
说白了，就是从求精确的逆矩阵改为最小化 AB 与 M 的平方误差。本系列的主题是低秩近似，所以下面假设 ，其机器学习意义就是通过低维的、有损的输入矩阵A和线性变换B来重建完整的M矩阵。

当 m=n 且 M 取单位阵 时，我们就得到一个只依赖于 A 的结果，记为

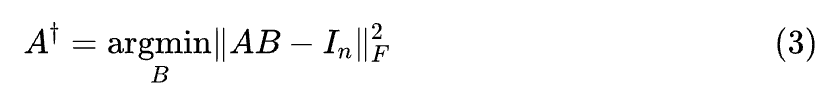
它的作用类似于 A 的逆矩阵，所以称为 A 的“(右)伪逆”。类似地，如果给定的是B矩阵，那么我们也可以将优化参数改为 A，得到 B 的“(左)伪逆”：

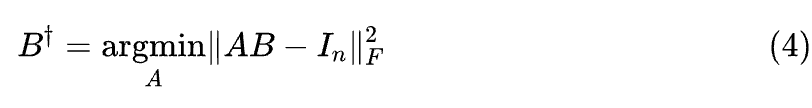
范数相关

在进一步推导之前，我们先补充一下 F 范数的相关介绍。向量的范数想必很多读者已经熟知，比较经典的就是“p-范数”：对于 ，其 p-范数定义为

而 p-范数中，最常见的就是 p=2 的情形，它就是我们经常说的向量模长，也叫“欧几里得范数”，如果省略范数的下标只写 ，那么基本上就是默认 p=2。

矩阵的范数稍微复杂一些，它至少有两种不同但都常用的范数，其中一种就是上一节已经提到的 F 范数，它是直接将矩阵展平为向量来计算的范数：

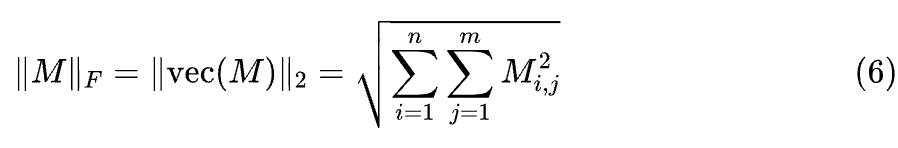
其他矩阵范数我们遇到时再作介绍。由于矩阵范数的多样性，所以 的下标 通常不能省略，以免引起混淆。F 范数是将矩阵当成向量然后照搬向量范数的定义而来的，由此启发我们可以尝试把更多的向量运算搬到矩阵中去，比如内积：

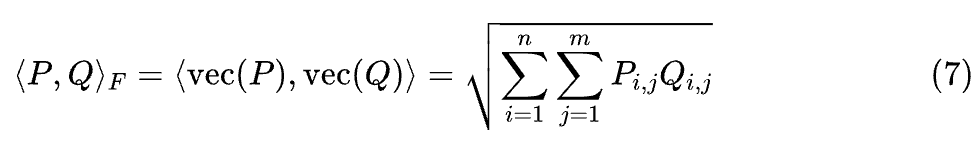
这称为矩阵 P,Q 的 F 内积（Frobenius Inner Product），其中 ，它可以用向量的迹运算来表示

这可以直接由矩阵乘法和迹的定义来证明（请读者尝试一下）。当 P,Q 是由多个矩阵连乘而来时，转换为等价的迹运算通常能帮助我们进行化简。比如，利用它我们可以证明正交变换不改变 F 范数：假设 U 是一个正交矩阵，利用以及 F 内积与迹的关系，得到

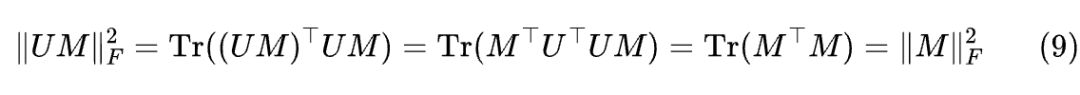
矩阵求导

言归正传，对于一个优化目标，最理想的结果自然是能够通过求导来求出解析解，而（1）正好能实现这一点！改结论可以简单“目测”出来：AB-M 是关于 B 的线性函数，所以 是关于 A 或 B 的二次函数，二次函数的最小值有解析解的。

要求 关于 B 的导数，首先要求 关于 E=AB-M 的导数，然后求 E 关于 B 的导数，最后通过链式法则组合起来，即

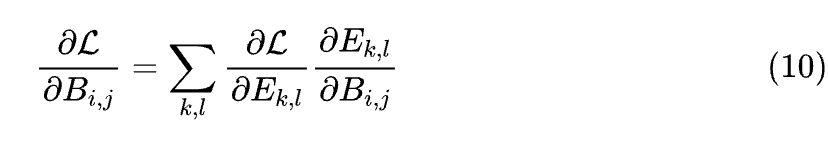
根据定义 ，很明显在求和的众多平方中只有当 (i,j)=(k,l) 时，关于 的导数才不为零，所以 关于 的导数就是 关于 的导数，即 ；接着，根据矩阵乘法的定义有

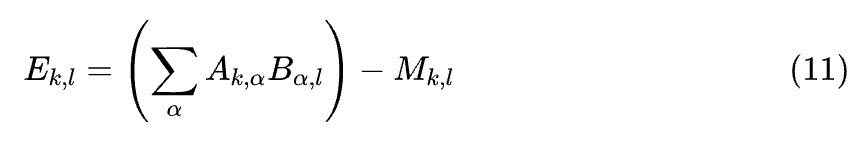
类似地，只有当 时，上式对 的导数才会产生非零的结果 ，所以我们可以写出 ，这里的 是 Kronecker 符号，用来声明 l=j 的条件。将结果组合起来，我们就得到

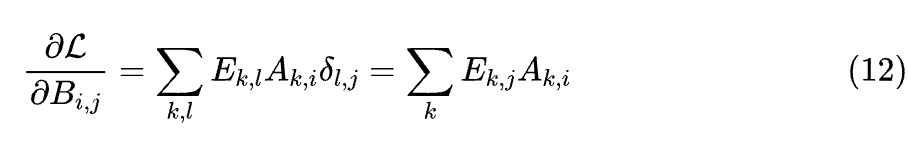
如果我们约定，标量对矩阵的梯度形状跟矩阵本身一致，那么可以写出

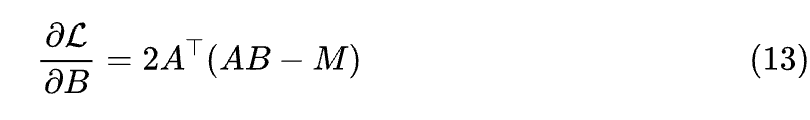
虽然推导过程破费周折，但好在结果还是很直观的：直觉上 就是 2(AB-M) 与 A 的乘积（类比标量求导），而我们已经约定 形状跟 B 形状一致（即 ），所以就要想办法通过 和 相乘来凑出一个 的结果来，结果就只有上式右端一种方式。根据同样原理，我们可以快速写出

基本结果

现在我们已经分别求出了 和 ，让它们等于零便可以解出相应的最优解

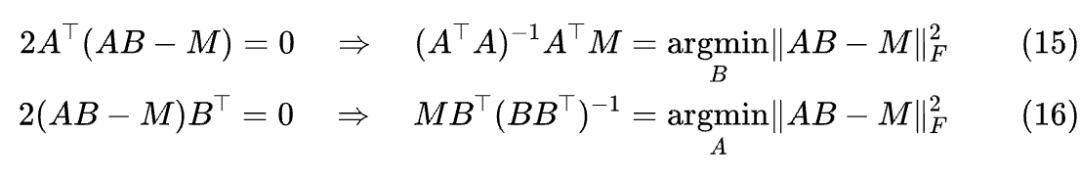
代入 ，就得到

如果 A 或 B 是可逆方阵，那么容易证明伪逆就等于逆矩阵，即 。此外，根据上式我们还可以验证：

1. ，即伪逆的伪逆等于自身，这意味着伪逆在作为近似逆矩阵的同时，保全了自身的信息；

2. ，即 虽然没法成为单位阵 I，但对 来说它们起到了单位阵的作用。

顺便说一下，矩阵的伪逆实际上是一个很宽泛的概念，它有很多种不同的形式，这里我们介绍的实际上是最常见的“Moore–Penrose 逆 [1]”，除此之外还有“Drazin 逆”、“Bott–Duffin 逆”等，但这些笔者也不了解，所以就不作展开，读者可以自行参考维基百科的“广义逆 [2]”条目。

一般形式

不过，事情还没完。式（17）、（18）成立还有个关键前提是相应的 或 可逆，如果不可逆呢？

我们以 为例，假设 不可逆，那么意味着 A 的秩不足 r，我们只能从中找到 个列向量构成的极大线性无关组构成矩阵 ，然后A可以表示成 ，其中 是 到 A 的矩阵。此时

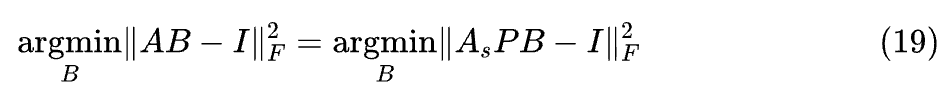
如果 B 的最优解仍然记为 ，那么我们只能确定

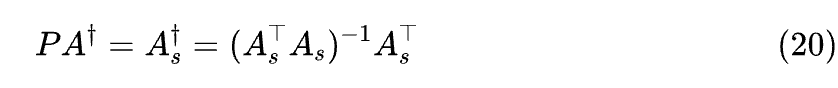
由于已经假设了 是极大线性无关组，所以 必然可逆，因此上式是良好定义的。然而，从 到 是一个降维到过程，这意味着存在多个 使得 ，即此时目标（3）的最优解并不唯一，换言之当 不可逆时我们无法只凭目标（3）来确定唯一的伪逆 。

一个可能的思路是补充 或 ，这样结合 就可以唯一地确定 。然而，这样打补丁的味道太浓了，实际上我们可以用一个精妙的技巧更优雅和统一地处理这个问题。问题出在当 不可逆时，目标函数（3）不是严格正定的，我们可以加上一个正则项让它变得正定，求出结果后再让正则项的权重趋于零：

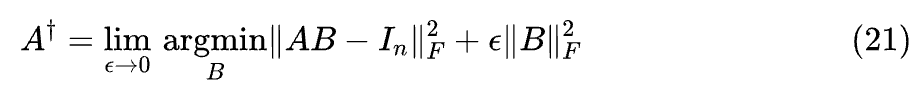
这里 ， 是指正向趋于零。由上式可以解得

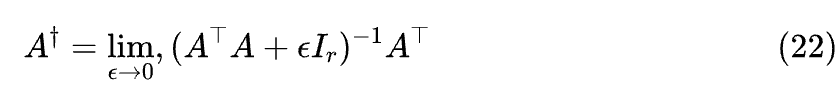
当 时， 必然是可逆的（请读者证明一下），因此上式是良好定义的。由于 时，正则项可以忽略不计，所以上述极限必然是存在的。注意，这里说的是整体极限的存在性，当 不可逆时，极限 是不存在的（结果会出现无穷大），只有乘上 后整体再取极限才是正常的。

式（22）作为伪逆的一般推广有什么优点呢？首先，我们已经有了 可逆时的 表达式（17），式（22）作为它的推广，具有直观且形式一致的理论优雅性；其次，形式上的一致也使得 可逆时 的性质如 能够得以保留，从而让我们在讨论 时几乎可以完全不考虑 的可逆性。

数值计算

当然，目前的式（22）只是一个形式化的定义，如果直接利用它来数值计算的话，就必须取一个足够小的 然后把 算出来，这样必然会面临严重的数值不稳定性。为了得到一个稳定的计算方式，我们利用实对称矩阵总可以正交对角化这一特点（谱定理 [3]），对 作如下分解：

其中 U 是正交矩阵，是特征值组成的对角矩阵，由于 的半正定性，它的特征值总是非负的。利用这个分解，我们有

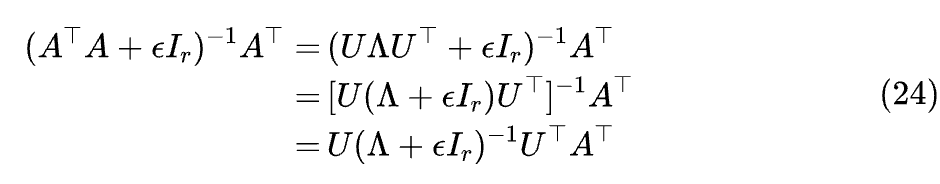
对于 我们有

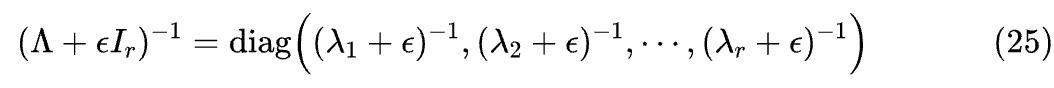
如果 ，那么 ，这是有限的结果，不妨碍计算，问题出现在 时 上。

然而，我们知道 时正则项的影响就会消失，所以断定极限（22）必然不会出现无穷大值，因此如果存在 ，那么右端所乘的 必然有办法抵消 带来的无穷大。而能抵消这种无穷大的，唯有“乘以 0”，即 。

换句话说，如果 ，那么 给 所乘的因子必然是 0。既然如此，由于“0 乘任何数都得 0”，所以其实 时 的取值反而不重要，我们可以简单地让它等于 0。这样一来，我们就得到了一种通用的计算 的简单方法：

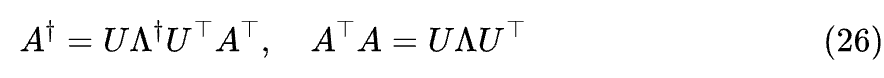
其中 表示对角线上的元素如果等于零则不变，非零则取倒数。

可能有读者疑问，既然“0 乘任何数都得 0”，那么为什么等于零的 要不变呢？随意取一个别的值可以吗？其实这里随便取一个值也不会影响结果的，但由于我们用了 这个记号，那么就要保持它跟式（22）的一致性，即它跟将对角阵 代入式（22）的直接计算结果要一致

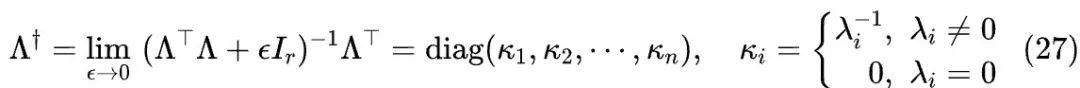
文章小结

在这篇文章中，我们从低秩近似的角度介绍了伪逆，这是逆矩阵概念对于非方阵或不可逆方阵的扩展，使我们可以更有效地分析和求解一般的矩阵方程。

参考文献

[1] https://en.wikipedia.org/wiki/Moore%E2%80%93Penrose_inverse 

[2] https://en.wikipedia.org/wiki/Generalized_inverse 

[3] https://en.wikipedia.org/wiki/Spectral_theorem

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·

·

·