物理光学华

north_)

已于 2024-10-17 09:59:40 修改

阅读量1.8k

点赞数 32

文章标签：笔记

于 2024-10-11 11:35:12 首次发布

本文链接：https://blog.csdn.net/cai_han_xu/article/details/142846059

版权

光的电磁理论

场

有一个区域V，域内每一点M都对应着一个确定的物理量，这时确定了这个物理量的一个场。

如果确定的是数量，则称为标量场；若确定的物理量是矢量，则称为矢量场。

梯度

标量场 f(x,y,z) 在某点M(x,y,z)的梯度是一个矢量，记作：

$\nabla f(x,y,z) = \frac{\partial f}{\partial x} \vec x_0 + \frac{\partial f}{\partial y} \vec y_0 + \frac{\partial f}{\partial z} \vec z_0$

微分算符 $\nabla$ （哈密顿算符/nabla算子）定义为:

$\nabla = \frac{\partial }{\partial x} \vec x_0 + \frac{\partial }{\partial y} \vec y_0 + \frac{\partial }{\partial z} \vec z_0$

标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。

散度

矢量函数F(M)在P点通量对体积的变化率：

$\lim_{\Delta V \to 0}{\frac{\oint_{S} A \cdot \,dS}{\Delta V}} = \nabla \cdot A$ 曲面积分是指的通量

散度记作：

$\nabla \cdot F = ( \frac{\partial }{\partial x} \vec x_0 + \frac{\partial }{\partial y} \vec y_0 + \frac{\partial }{\partial z} \vec z_0) \cdot (P \vec x_0 + Q \vec y_0 +R \vec z_0) = (\frac{\partial P}{\partial x} +\frac{\partial Q}{\partial y} +\frac{\partial R}{\partial z} )$

矢量的散度是通量体密度，即通过包围单位体积闭合面的通量。

旋度

矢量函数F(M)旋度：大小为环流面密度的最大值，方向为是环流面密度去最大值时面元的法线方向。

$\lim_{\Delta S \to 0}{\frac{\oint_{L}A\cdot \,dl}{\Delta S}} = (\nabla \times A) \cdot \hat n = (\nabla \times A)_n$

定义为微分算符 $\nabla$ 与矢量F的矢量积，即：

$\nabla \times F = \begin{vmatrix}\vec x_0 & \vec y_0 & \vec z_0 \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ P& Q & R \end{vmatrix} = (\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z})\vec x_0 + (\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x})\vec y_0 + (\frac{\partial Q}{\partial z} - \frac{\partial P}{\partial y})\vec z_0$

矢量的旋度是环流面密度的最大值，与面元的取向有关。表示曲线、流体等旋转程度的量。

矢量分析基本公式

$\nabla \times (\nabla f) = 0$ 梯度场必是无旋场

$\nabla\cdot(\nabla\times F)=0$ 旋度场必是无散场

$\nabla\cdot(\nabla f)=\nabla^{2}f$

$\nabla\times(\nabla\times F)=\nabla(\nabla\cdot F)-\nabla^{2}F$

高斯定理

空间区域上三重积分与其边界上曲面积分之间关系的定理。

$\iiint_{V}\nabla\cdot FdV=\iint_{S}F\cdot ds$

对散度场进行积分等于穿过这个区域表面积的通量

斯托克斯定理

关于曲面积分与其边界曲线积分之间关系的定理。

$\iint_{\mathfrak{s}}\nabla\times Fds=\int_{\mathfrak{l}}F\cdot dl$

对旋度场进行积分等于通过其环路的通量

亥姆霍兹定理

① 一个矢量场的性质可完全由它的散度和旋度来表明。

②无旋场的散度不能处处为0，无散场的旋度也不能处处为0，否则矢量场就不存在。

③任何一个矢量场都必须有源，散度对应发散源，旋度对应漩涡源

一个矢量场可分成一个无旋度散场和一个无散度旋场的叠加，即 $A = A_1 + A_2$

其中无旋场分量 $A_1$ 的散度不为0，设为 $\rho$ ,无散场分量 $A_2$ 的旋度不等于0，设为J,则：

$\nabla\cdot A=\nabla\cdot(A_{1}+A_{2})=\nabla\cdot A_{1}=\rho$

A的散度代表着形成矢量场的一种源——标量源

$\nabla\times A=\nabla\times(A_{1}+A_{2})=\nabla\times A_{2}=J$

A的旋度代表着形成矢量场的一种源——矢量源

积分形式

$\oint_{S}A\cdot dS=\int_{V}\rho dV$

$\int_{l}A\cdot dl=\int_{s}J\cdot dS$

麦克斯韦方程组

方程（1）为推广的安培环路定理，表明传导电流和随时间变化的电场都能产生磁场。

方程（2）为电磁感应定律，表明变化的磁场能产生电场。

方程（3）为磁通连续定理，表明磁场是无源场，磁力线总是闭合曲线。

方程（4）为高斯定律，表明电荷以发散的方式产生电场。

物理意义：

①时变电场的激发源除了电荷以外，还有变化的电场；时变磁场的激发源除了传导电流以外，还有变化的电场。

②电场和磁场互为激发源，相互激发。

③电场和磁场不再相互独立，而是相互关联，构成一个整体——电磁场，电场和磁场分别为电磁场的两个物理量。

④麦克斯韦方程组预言了电磁波的存在，且已被事实证明。

静态场

$\vec{F}=q\cdot\vec{E}$ 是电场对存在于其中的电荷有力的作用

$\vec{F}=q\nu\times\vec{B}$ 磁感应强度作用在运动的电荷上产生洛伦兹力

$\iint_{S}\vec{D}\cdot d\vec{S}=q$ 对电感应强度D做一个封闭面上的通量积分，就是它的源-电荷

$\oint_{l}\bar{H}\cdot d\vec{l}=I$ 对磁场做一个环路积分，它的源是电流或变化电场

物质方程

由物质属性有关 $\chi_e$ 是电极化率， $\chi_m$ 是物质的磁化率， $\sigma$ 是电导率

线性与非线性光学

各向异性的张量：

乘积形式

导致D与E的方向不再平行

时谐电磁场

时谐场：随时间按正弦或余弦规律变化的场矢量。

Re是一个取实部的操作符

优点：

复振幅：

麦克斯韦方程组的复数形式

边值关系

①在交界面上 $\varepsilon$ 、 $\mu$ 和 $\sigma$ 的突变引起电磁场的突变

②在两种介质的分界面上电磁场量通常是不连续的

③在没有面电荷和面电流的情况下，界面处B和D的法向分量以及H和E的切向分量是连续的

求穿过圆柱体的B和D的通量，即对散度进行积分

由高斯定理， $\iiint_v\nabla \cdot \vec B\,dv = \iint_s \vec B \,ds$ ，对应麦克斯韦方程组的积分形式的第三项为0

而对圆柱体穿过表面积的通量可分为上，下和侧边通量，在边界上 $\Delta h$ 趋近于0，可以省略掉，我们就能得到在上表面和下表面通量相加为0，又因为第二个面的法向是负的，我们可以写成

$\vec B_{1n} \cdot \Delta S_1 - \vec B_{2n} \cdot \Delta S_2 = (\vec B_{1n} - \vec B_{2n}) \cdot \Delta S = 0$ n代表与分界面垂直

即 $\vec B_{1n} = \vec B_{2n}$

同样由高斯定理和麦克斯韦方程组积分形式第三项，我们可以得到：

$\iiint_v \nabla \cdot \vec {D} \,dv = \iint_s \vec D \,ds = Q$

而Q和分界面中的电荷有关，我们用电荷面密度 $\sigma_s$ 来表示。当 $\Delta h$ 趋近于0，同上上式可推导出 $\vec n(\vec D_2 - \vec D_1) = \sigma_s$

即 $D_{2n} - D_{1n} = \sigma_s$

计算穿过环路的通量，即对旋度进行积分

由斯托克斯定理 $\iint_s \nabla \times \vec E \,ds = \int_l \vec E \,d{\vec l}$ , 由麦克斯韦方程组积分形式第二项得

$\int_l \vec E \,d{\vec l} = - \iint_s \frac{\sigma B}{\sigma t} \,ds$ 当 $\Delta h$ 趋于0是，s面积也趋于0，整个式子趋于0

后续分析与上方一样。

总结：

如果整个空间没有传导电流和自由电荷，则可以写成右边的形式

电磁场的能量

时变电磁场中的一个重要现象就是电磁能量的流动。

定义单位时间内穿过与能量流动方向垂直的单位表面的能量为能流密度矢量

能流定理

能流矢量等于电场叉乘磁场

光波与介质的基本性质

平面电磁波

电场或磁场在与传播方向正交的平面上各点具有相同值的波。

式中相位有关于空间方面的部分 $\phi_r = \frac{2\pi}{\lambda} \cdot z$ 代表着每隔一个波长就是一个周期

有关时间的部分 $\phi_t = \frac{2\pi}{\lambda} \cdot vt = 2\pi f t = \frac{2\pi}{T}t$ 代表每个一个周期波又回到初始的状态

波矢量

一般坐标系下的波函数

把空间位置矢量 r 与新波矢量K0进行点乘，将它投影到新的坐标轴s上

复数形式

复振幅

平面电磁波的性质

球面波和柱面波

光的吸收

复折射率

平面波的叠加

光的偏振

光波是横波，其光矢量的振动方向与光波传播方向垂直。在垂直传播方向的平面内，电厂强度矢量还可能存在各种不同的振动方向，称之为光的偏振。

偏振是横波区别于纵波的一个明显标志。

可由两个矢量合成一个新的矢量来看，由于两个线偏振光的矢量都是不断变化的，所以合成的新偏振光的矢量和方向都在不断的变换，即为圆或椭圆偏振光。

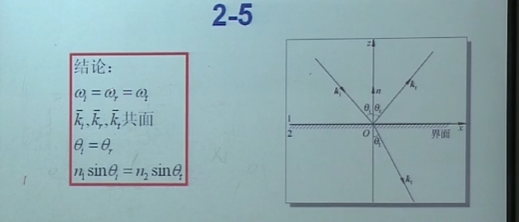
光的反射和折射

推到出来，入射，反射和折射共面，这个面成为入射面。