LeetCode 347. Top K Frequent Elements 解题报告

LeetCode 347. Top K Frequent Elements 解题报告

题目描述

Given a non-empty array of integers, return the k most frequent elements.

---

示例

Given [1,1,1,2,2,3] and k = 2, return [1,2].

---

注意事项

• You may assume k is always valid, 1 ≤ k ≤ number of unique elements.
• Your algorithm’s time complexity must be better than O(n log n), where n is the array’s size.

---

解题思路

我的思路：

不得不说，这道题，我的解法很绕。我的思路是：
1.将原来的数组进行排序
2.遍历数组，遍历过程中记下每个数字出现的次数，将(数字，出现次数)这一组信息保存在一个vector里
3.按照出现次数由多至少对vector的元素进行排序
4.保存vector的前k个元素到存储结果的数组中，返回存储结果的数组。

通过了肯定得看看其他人是怎么做的，好吧，看完了真心感觉自己在算法上有很大的缺陷，大牛们用到了不同的算法跟数据结构去完成这道题，下面我一个个来实现一次。

参考思路：

桶排序

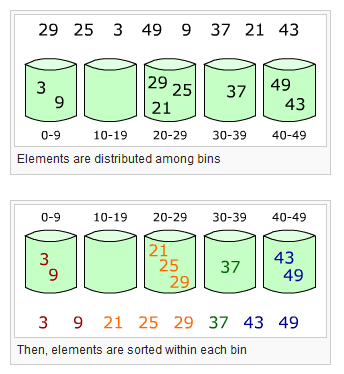
桶排序算法大概的过程是将数据分到不同的桶中，这些桶都是有序，然后对桶内的元素排序，最后从第一个桶开始把所有元素串起来就是一个有序的数列，见下面wiki中的图：

那桶排序算法是怎样用在这道题里的呢？答案是利用了桶之间有序的特性。

• 首先用一个unordered_map存储数组中每个元素及其出现的次数。
• 然后构建桶结构，（其实就是vector组成的二维数组），桶的序号设为出现次数，即1号桶表示出现1次，2号桶表示出现2次，依次类推（这就是为什么代码里构建桶时是unordered_map长度+1的原因，0号桶不用，最多次数为unordered _map的长度）
• 然后根据数字出现次数把它们放到相应的桶内，完成这一步之后各个数字就已经是有序了。
• 最后从最后一个桶开始（因为最后一个桶表示出现次数最多），倒序地把各个桶内的数字放入到结果数组中，直到结果数组刚好有k个元素。
  实现见参考代码1，代码很直观易懂。

堆结构

这道题还可以用堆这个数据结构来完成，基本思想是利用了堆以一定的偏序保存节点的特性，下面讲述利用最大堆和最小堆的实现。
两个实现第一步都是用unordered_map保存数字及其出现的次数。
最大堆：堆中保存的是次数最大的k个数字。不断地向堆放入数据，当堆中元素超过k时就弹出数据，此时被弹的数据是堆中出现次数最小的数字。最后将堆中剩下的元素返回。实现中使用了vector以及make_heap，pop_heap函数。见参考代码2。
最小堆：堆中保存的是次数最小的n-k个数字，n为unordered_map的大小。不断地向堆放入数据，当堆中元素超过n-k时就弹出数据，此时被弹的数据是堆中出现次数最大的数字，因为n-k个次数小的在堆中，所以被弹出的就是k个最大的元素，保存被弹出的数据。最后这些数据返回。实现中使用了优先队列priority_queue作为堆结构，见参考代码3。

---

代码

我的代码

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        vector<pair<int, int> > freq;
        vector<int> kFrequent;

        sort(nums.begin(), nums.end());

        nums.push_back(nums[nums.size() - 1]);
        for (int i = 0, j = 1, count = 0; j < nums.size();) {
            if (nums[i] != nums[j] || j == nums.size() - 1) {
                count = j - i;
                freq.push_back(pair<int, int>(nums[i], count));
                i = j;
                j++;
            } else {
                j++;
            }
        }

        sort(freq.begin(), freq.end(), [](pair<int, int>a, pair<int, int>b) {
            return a.second > b.second;
        });

        for (int i = 0; i < k; i++) {
            kFrequent.push_back(freq[i].first);
        }

        return kFrequent;
    }
};

参考代码1：桶排序

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int, int> htable;

        for (auto n: nums)
            htable[n]++;

        vector<vector<int>> bucket(nums.size() + 1);

        for (auto h: htable)
            bucket[h.second].push_back(h.first);

        vector<int> ans;    
        for (int i = bucket.size() - 1; i>=0 && ans.size() < k; i--) {
            for (int j = 0; j < bucket[i].size(); j++) {
                ans.push_back(bucket[i][j]);
                if (ans.size() == k) 
                    break;
            }
        }

        return ans;
    }
};

参考代码2：最大堆

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int, int> htable;

        for (auto n: nums)
            htable[n]++;

        vector<pair<int, int>> heap;
        for (auto h: htable) 
            heap.push_back({h.second, h.first});

        make_heap(heap.begin(), heap.end());
        vector<int> ans;
        while(k--) {
            ans.push_back(heap.front().second);
            pop_heap(heap.begin(), heap.end());
            heap.pop_back();
        }

        return ans;
    }
};

参考代码3：最小堆

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int, int> htable;

        for (auto n: nums)
            htable[n]++;

        // pair(frequency, number)
        priority_queue<pair<int, int>> heap;
        vector<int> ans;
        for (auto p: htable) {
            heap.push({p.second, p.first});
            if (heap.size() > htable.size() - k) {
                ans.push_back(heap.top().second);
                heap.pop();
            }
        }

        return ans;
    }
};

---

总结

这道题让我学了很多知识，复习了桶排序，堆数据结构，以及STL中一些函数和容器的使用，多做题真的是能学到东西。做题关键的还是要灵活运用自己学过的算法和数据结构，以后自己要多加注意。
填坑真快乐~继续加油！