《编程珠玑(第2版)》笔记——将一个n元一维向量向左旋转i个位置（第2章）

第2章 啊哈！算法

《编程珠玑(第2版)》的第2章，一开始就给出三个问题，其中问题B很有意思：将一个n元一维向量向左旋转i个位置。例如，当n=8且i=3时，向量abcdefgh旋转为defghabc。简单的代码使用一个n元的中间向量在n步就能够完成该工作，你能否仅使用数十个额外字节的存储空间，正比于n的时间内完成向量旋转。

其实就像问题中提到的，如果不考虑空间，这是个很简单的问题。但考虑到空间的时候，能否灵巧地解决该问题？

 

首先：在我看来没有必要写这么复杂，很简短很简单就能实现。

给我我个人方法：

#include "stdio.h"
#include "stdlib.h"
void main()
{
 char *p;
 int n,m,i=0;
 printf("字符串长度n为:");
 scanf("%d",&n);
 p = (char*)malloc(n+1);
 printf("输入字符串：");
 scanf("%s",p);
 printf("要转换的长度为：n = ");
 scanf("%d",&m);
 m = m % n;
 printf("%s",p+m);
 while (m > 0)
 {
  printf("%c",p[i++]);
  m--;
 }
 printf("\n");
 free(p);
}

书中给出了2个比较精巧的方法：

1.求模置换的方法：

其实我们知道有个节约空间的方案：每次向左旋转一个位置（其时间正比于n），总共需要旋转i次。这个方案会消耗过多的运行时间。而求模置换的方法则是尽量让每个数一次移动到位。总体的思想是:以i为除数对n求模，将向量遍历完并一次移动到位。看下面两个例：

示例数组： {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

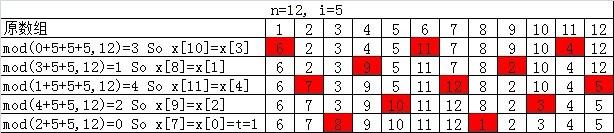
(1)n=12且i=5：

(2)n=12且i=3：

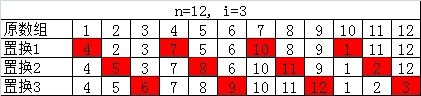
上述两图展示了两种不同的情况，示例(1)的n=12和i=5最大公约数是1，因此不断求模能够无重复完整遍历数组；而示例(2)中n=12且i=3，有最大公约数3，因此移动3个位置就会出现重复，因此需要移动到下一位再次求模共3次：

 

[cpp] view plain copy print ?

1. //求公约数  
2. unsigned int Gcd(unsigned int a, unsigned int b)  
3. {  
4.     unsigned int temp;  
5.     while (b != 0)  
6.     {  
7.         temp = a % b;  
8.         a = b;  
9.         b = temp;  
10.     }  
11.   
12.     return a;  
13. }  
14.   
15. void modShift(int array[], int n, int rotdist)  
16. {  
17.     unsigned int gcd = Gcd(n, rotdist);  
18.   
19.     for (int i = 0; i < gcd; i ++)  
20.     {  
21.         int temp = array[i];  
22.         int j = i;  
23.         int k;  
24.         while(1)  
25.         {  
26.             int k = j +  rotdist;  
27.             if (k >= n)  
28.             {  
29.                 k -= n;  
30.             }  
31.               
32.             if (k == i)  
33.             {  
34.                 break;  
35.             }  
36.   
37.             array[j] = array[k];  
38.             j = k;  
39.         }  
40.         array[j] = temp;  
41.     }  
42.   
43. }  

//求公约数
unsigned int Gcd(unsigned int a, unsigned int b)
{
	unsigned int temp;
	while (b != 0)
	{
		temp = a % b;
		a = b;
		b = temp;
	}

	return a;
}

void modShift(int array[], int n, int rotdist)
{
	unsigned int gcd = Gcd(n, rotdist);

	for (int i = 0; i < gcd; i ++)
	{
		int temp = array[i];
		int j = i;
		int k;
		while(1)
		{
			int k = j +  rotdist;
			if (k >= n)
			{
				k -= n;
			}
			
			if (k == i)
			{
				break;
			}

			array[j] = array[k];
			j = k;
		}
		array[j] = temp;
	}

}

 

2.分段递归交换的方法：

旋转向量x其实就是交换向量ab的两段，得到ba（a代表x中的前i个元素）。假设a比b短，将b分为b1和b2两段，使b2有跟a相同的长度，然后交换a和b2，也就是ab1b2交换得到b2b1a，a的位置已经是最终的位置，现在的问题集中到交换b2b1这两段，又回到了原来的问题。不断递归下去，到b1和b2的长度长度相等交换即可。代码如下

[cpp] view plain copy print ?

1. //swapShift  
2. //swap x[a .. a+offset-1] and x[b .. b+offset-1]  
3. void swap(int array[], int a, int b, int offset)  
4. {  
5.     int temp;  
6.     for (int i = 0; i < offset; i++)  
7.     {  
8.         temp = array[a + i];  
9.         array[a + i] = array[b + i];  
10.         array[b + i] = temp;  
11.     }  
12. }  
13.   
14.   
15. void swapShift(int *array, int n, int rotdist)  
16. {  
17.     int p = rotdist;  
18.     int i = p;  
19.     int j = n - p;  
20.   
21.     while (i != j)  
22.     {  
23.         if (i > j)  
24.         {  
25.             swap(array, p - i, p, j);  
26.             i -=j;  
27.         }  
28.         else  
29.         {  
30.             swap(array, p - i, p + j - i, i);  
31.             j -= i;  
32.         }  
33.     }  
34.     swap(array, p - i, p, i);  
35. }  

//swapShift
//swap x[a .. a+offset-1] and x[b .. b+offset-1]
void swap(int array[], int a, int b, int offset)
{
	int temp;
	for (int i = 0; i < offset; i++)
	{
		temp = array[a + i];
		array[a + i] = array[b + i];
		array[b + i] = temp;
	}
}


void swapShift(int *array, int n, int rotdist)
{
	int p = rotdist;
	int i = p;
	int j = n - p;

	while (i != j)
	{
		if (i > j)
		{
			swap(array, p - i, p, j);
			i -=j;
		}
		else
		{
			swap(array, p - i, p + j - i, i);
			j -= i;
		}
	}
	swap(array, p - i, p, i);
}

 

3.求逆法（翻手算法）

利用向量原理：把x向量分成ab两部分，a是前i个元素，b是后n-i个元素，首先对a求逆，得到a-1b，然后对b求逆得到a-1b-1，然后对整体求逆得到（a-1b-1）-1=ba。

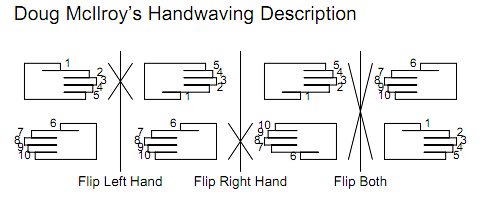
非常容易理解，代码如下：

[cpp] view plain copy print ?

1. //Reverse  
2. void reverse(int array[], int low, int high)  
3. {  
4.     int temp = 0;  
5.     for(int i = low; i <= (high + low) / 2; i++)  
6.     {  
7.         temp = array[i];  
8.         array[i] = array[high - (i - low)];  
9.         array[high - (i - low)] = temp;  
10.     }  
11. }  
12.   
13. void reverseShift(int *array, int n, int rotdist)  
14. {  
15.     reverse(array, 0, rotdist - 1);  
16.     reverse(array, rotdist, n - 1);  
17.     reverse(array, 0, n - 1);  
18. }  

//Reverse
void reverse(int array[], int low, int high)
{
	int temp = 0;
	for(int i = low; i <= (high + low) / 2; i++)
	{
		temp = array[i];
		array[i] = array[high - (i - low)];
		array[high - (i - low)] = temp;
	}
}

void reverseShift(int *array, int n, int rotdist)
{
	reverse(array, 0, rotdist - 1);
	reverse(array, rotdist, n - 1);
	reverse(array, 0, n - 1);
}

 

翻手算法代码非常简短，非常容易理解，而且针对字符串的求逆也不用自己写函数，在时间和空间上都很高效。

 

总结：

一个简单的问题，在不同的角度，可以找到不同的方法，主要要做到发散思维，找到高效又容易理解的方法。