4.12 求和路径

     《程序员面试金典》（第六版）习题：仅为记录一下以加强印象，不为商业用途，如有侵权请联系删除。以下源码和解释参考了书中源码以及解释。
     以下蛮力法利用递归统计从二叉树中每一个节点开始的满足题设要求的路径数，然后求其和即为所求。当二叉树平衡的时候，计算从根节点（第一层）开始的满足题设要求的路径数时大约需要递归调用函数$countPathWithSumFromNode$的次数为$N-1=N-2^1-1$，计算从二叉树的的第二层节点的开始的满足题设要求的路径数时大约需要递归调用函数$countPathWithSumFromNode$的次数为$N-3=N-2^2-1$，以此类推计算从二叉树的的最低一层节点的开始的满足题设要求的路径数时大约需要递归调用函数$countPathWithSumFromNode$的次数为$N-N=N-2^{log{2}^{N-1}}-1$。因此算法的时间复杂度约$O(N\ast log{2}^N-(2^1+2^2+..+2^{log{2}^N})-log{2}^N)=O(N\ast log{2}^N-2^{log{2}^N+1}-2-log{2}^N)=O(N\ast log{2}^N-2\ast N-2-log{2}^N)=O(N\ast log{2}^N)$

class BinaryNode
{
    private:
    	int data;
    	BinaryNode* left;
    	BinaryNode* right;
    public:
    	BinaryNode(int value = 0, BinaryNode* pointer1 = nullptr, BinaryNode* pointer2 = nullptr)
    	{
    		data = value;
    		left = pointer1;
    		right = pointer2;
    	}
    	BinaryNode* getLeft()
    	{
    		return left;
    	}
    	BinaryNode* getRight()
    	{
    		return right;
    	}
    	int getData()
    	{
    		return data;
    	}
};
int countPathWithSumFromNode(BinaryNode* node, int targetSum,int currentSum)
{
	if (node == nullptr)
		return 0;
	currentSum = currentSum + node->getData();
	int totalPaths = 0;
	if (currentSum == targetSum)
	{
		totalPaths++;
	}
	totalPaths += countPathWithSumFromNode(node->getLeft(), targetSum, currentSum);
	totalPaths += countPathWithSumFromNode(node->getRight(), targetSum, currentSum);
	return totalPaths;
}
int countPathWithSum(BinaryNode* root,int targetSum)
{
	if (root == nullptr)
		return 0;
	int pathsFromRoot = countPathWithSumFromNode(root, targetSum, 0);

	int pathsOnLeft = countPathWithSum(root->getLeft(), targetSum);
	int pathsOnRight = countPathWithSum(root->getRight(), targetSum);
	return pathsFromRoot + pathsOnLeft + pathsOnRight;
}

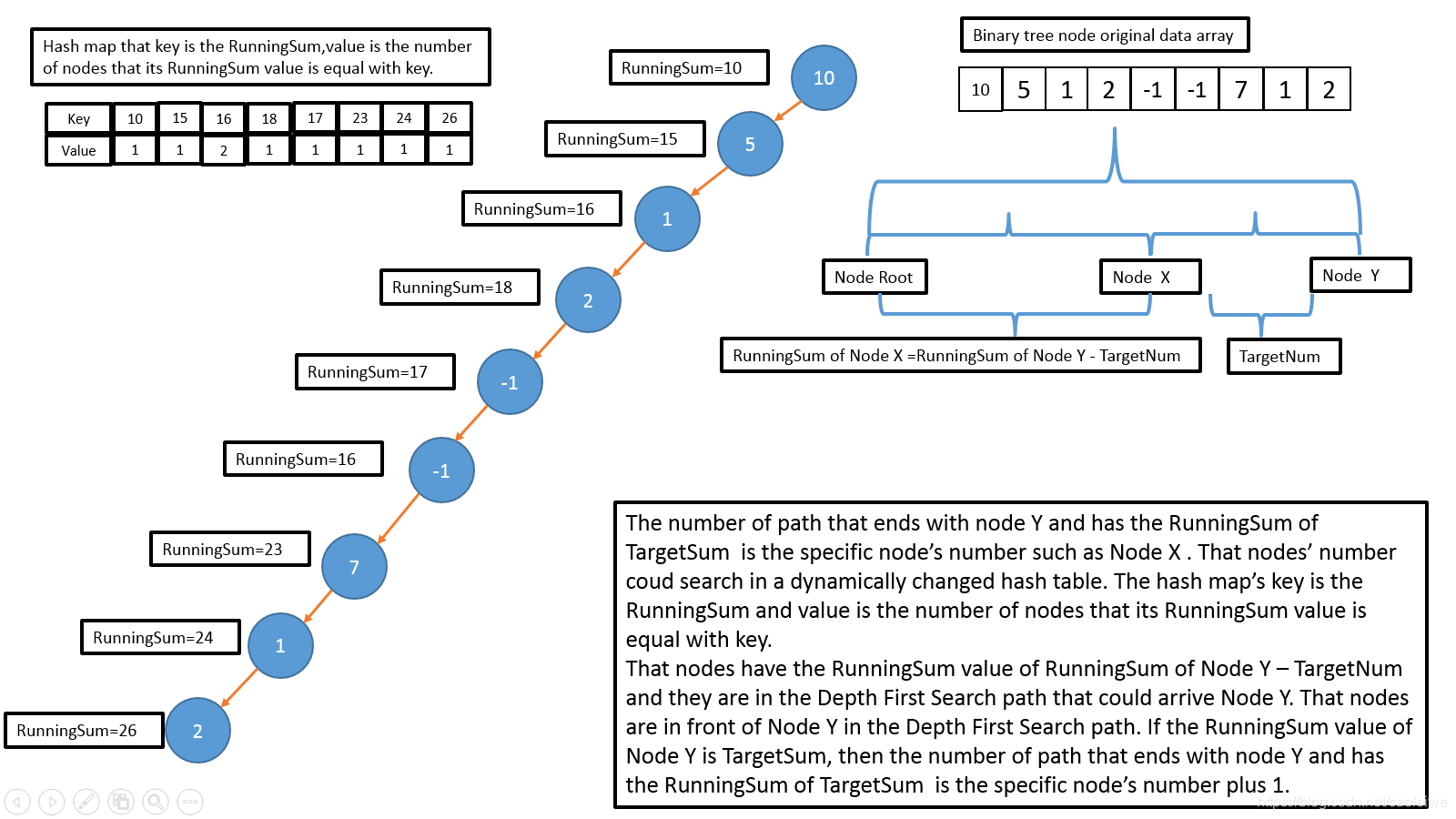
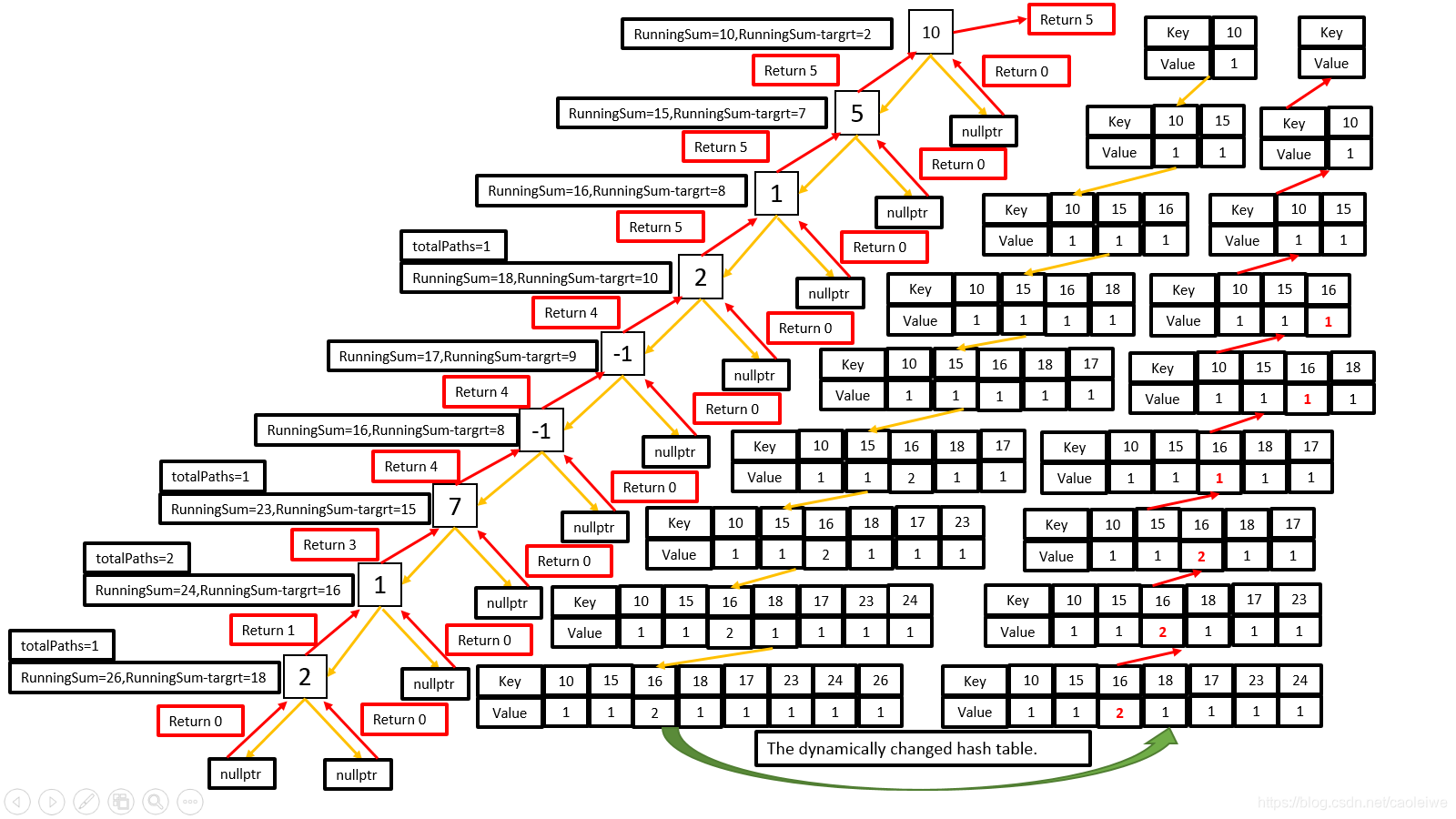
     以下优化算法和以上蛮力法的运作方向相反，它是统计树中以每一个节点为终点的满足题设要求的路径的个数，然后对所有节点的返回值求和即为所求。优化算法从根节点开始对二叉树进行深度优先搜索，到达一个节点时其$RunningSum$的值为包含该节点值以及路径中该节点之前的所有节点值之和。这个过程中还会动态维持一个哈希表，每当进入一个节点时，如果没有以其$RunningSum$为键值的元素存在于哈希表中，则插入以该$RunningSum$为键值的元素，其值为1。如果哈希表中存在该键值则将其相应的值加一。每当从一个节点返回时将哈希表中以该$RunningSum$为键值的元素的值减一，如果减一后其值为0则删除以该$RunningSum$为键值的元素（这样做的目的是因为算法是在统计深度优先搜索路径中在该节点前面的满足要求的节点，当算法从一个节点返回时该节点就不会被算在包含深度优先搜索中下一个节点的路径中）。达到一个节点后以$RunningSum-targetNum$为键值在哈希表中查询其相应的值，则树中以该节点为终点的且满足题设要求的路径树即为该值，如果$RunningSum=targetNum$则还要在查询到的值得基础上加一。一个简单的例子以及其算法的递归过程如图1和图2所示。该算法的时间复杂度为$O(N)$，N为树中节点的个数。如果不考虑递归调用的函数栈空间则二叉树平衡时算法的空间复杂度为$O(lo{g}_2^N)$,对于非平衡树空间复杂度可以增长到$O(N)$。这里其实就是树的深度。

　

图1.

　

图2.

//实现代码
class BinaryNode
{
    private:
    	int data;
    	BinaryNode* left;
    	BinaryNode* right;
    public:
    	BinaryNode(int value = 0, BinaryNode* pointer1 = nullptr, BinaryNode* pointer2 = nullptr)
    	{
    		data = value;
    		left = pointer1;
    		right = pointer2;
    	}
    	BinaryNode* getLeft()
    	{
    		return left;
    	}
    	BinaryNode* getRight()
    	{
    		return right;
    	}
		void setLeft(BinaryNode* value)
		{
			left=value;
		}
    	int getData()
    	{
    		return data;
    	}
};

void incrementHashTable(unordered_map<int, int> &hashTable, int key, int delta)
{
	int newCount = 0+delta;
	if (hashTable.find(key) != hashTable.end())
	{
		newCount+= hashTable[key];
	}

	if (newCount == 0) 
	{
		hashTable.erase(key);		
	}
	else 
	{
		hashTable.erase(key);
		pair<int, int> newpair = { key, newCount};
		hashTable.insert(newpair);
	}
}

int countPathWithSum(BinaryNode* node, int targetSum, int runningSum, unordered_map<int, int>& pathCount)
{
	if (node == nullptr)
		return 0;
	runningSum += node->getData();

	int sum = runningSum - targetSum;
	int totalPaths = 0;
	if (pathCount.find(sum) != pathCount.end())
	{
		totalPaths = pathCount[sum];
	}

	if (runningSum == targetSum)
	{
		totalPaths++;
	}
	incrementHashTable(pathCount, runningSum, 1);
	totalPaths += countPathWithSum(node->getLeft(), targetSum, runningSum, pathCount);
	totalPaths += countPathWithSum(node->getRight(), targetSum, runningSum, pathCount);
	incrementHashTable(pathCount, runningSum, -1);
	return totalPaths;
}

int countPathWithSum(BinaryNode* root, int targetSum)
{
	unordered_map<int, int> pathCount;
	return countPathWithSum(root, targetSum, 0, pathCount);
}

//测试程序
int main()
{
	BinaryNode node10(10);
	BinaryNode node5(5);
	BinaryNode node1(1);
	BinaryNode node2(2);
	BinaryNode node_negative1(-1);
	BinaryNode node_negative2(-1);
	BinaryNode node7(7);
	BinaryNode node11(1);
	BinaryNode node22(2);
	node10.setLeft(&node5);
	node5.setLeft(&node1);
	node1.setLeft(&node2);
	node2.setLeft(&node_negative1);
	node_negative1.setLeft(&node_negative2);
	node_negative2.setLeft(&node7);
	node7.setLeft(&node11);
	node11.setLeft(&node22);
	cout<<"The total paths is "<<countPathWithSum(&node10, 8)<<".\n";
}

　

测试结果.