Dijkstra 计算两地间的最短距离

        这里使用Dijkstra(戴克斯特拉)算法，该算法起始点实际计算出到任一点的距离，计算两城市间的距离实际是一个副产物，所有一下图为例来说明，该图为无向图，顶点间所标数字即为两点之间的距离。

 

问题：求点D到点A的距离。

 初始状态：

                                     

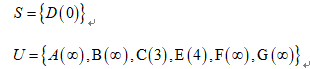
              集合S中 D(0)：D到D的距离为0；

              集合U中 A(∞)：D不能直接到达A；B(∞) ：D不能直接到达B；C(3)：D直接到达C的距离为3；E(4)：D直接到达E的距离为4；F(∞)：D不能直接到达F；G(∞)：D不能直接到达G。

 

第1步：由初始条件可以看出U集合中C到D的距离最小，故将C添加到集合S中，更新后，两集合关系如下：

                                   

         D到C的最小距离为：3，D到C的路线为：

                                                       

第2步：逐个判断集合S中元素到集合U中的距离，并将距离最小的点添加到集合S中

                  对A点 ：

                                      

                 对B点：

                                       

                对E点:

                                       

                对F点:

                                       

                对G点:

                                       

 由上可以看出  距离最小为4，将E添加到集合S中，更新后的集合如下：

                                  

  更新后，D到E的最短距离：4，D到E的最短路线为：

                              

 

第3步，逐个判断集合S中元素到集合U中的距离，并将距离最小的点添加到集合S中

               对A点：

                                 

              对B点：

                                 

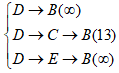
              对F点：

                                 

              对G点：

                                 

     由上可以看出，距离最小为6，故将F点加入到S集合中，更新后S和U分别为

                                  

     跟新后，D到F的最短距离为：6，最短路线为：

                                        

 

第4步：逐个判断集合S中元素到集合U中的距离，并将距离最小的点添加到集合S中

             对A点：

                             

            对B点：

                             

             对G点：

                            

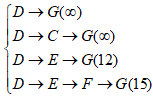
  由上可以看出，距离最小为12，故将G点加入到S集合中，更新后S和U分别为

                                

  更新后，D到G的距离最短：12，最短路线：

                           

第5步：逐个判断集合S中元素到集合U中的距离，并将距离最小的点添加到集合S中

          对A点：

                             

         对B点：

                          

由上可以看出，或距离最小为13，故将G点加入到S集合中，更新后S和U分别为

                                  

更新后，D到B的最短路线为：13，D到B最短路线为

                   或

 

第6步：逐个判断集合S中元素到集合U中的距离，并将距离最小的点添加到集合S中

          对A点(D到B的最短路线有2条，我们可以任选一条，这里选D→C→B)

                                 

           由上可以看出， 距离最小为22，故将G点加入到S集合中，更新后S和U分别为

                               

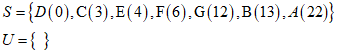
           更新后，D到A的最短路线为：22，D到B最短路线为