2阶回旋矩阵
1 2
4 3
3阶回旋矩阵
1 2 3
8 9 4
7 6 5
4阶回旋矩阵
1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7
一.对称分析法
N阶矩阵,意味着从外至内一共有N/2向下取整个空心矩阵,比如4阶矩阵,就由内外两个子矩阵组成。
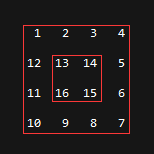
而对于每个子矩阵,可以采用上下和左右对称分析,如下图。
箭头不代表方向,因为QQ截图画不出直线。对于最外层的子矩阵,上边的1、2、3、4和下边的7、8、9、10;左边的11、12和右边5、6可以对称分析。
代码如下。
#include <iostream>
#include <iomanip>
using namespace std;
int matrix(int i, int j, int n);
int main()
{
int n, i, j, num=1;
cout << "Please input N:";
cin >> n;
int a[100][100]={0};
for(int m=0;m<n/2;m++)//n阶矩阵,意味着从外至内一共有n/2向下取整个矩阵;
{
for(j=m;j<n-m;j++)//上
{
a[m][j]=num++;
}
for(i=m+1;i<n-m-1;i++)//右
{
a[i][n-m-1]=num++;
}
for(j=n-m-1;j>=m;j--)//下
{
a[n-m-1][j]=num++;
}
for(i=n-m-2;i>=m+1;i--)//左
{
a[i][m]=num++;
}
}
if(n%2==1)//当阶数%2=1时,最中间的数值
{
a[n/2][n/2]=n*n;
}
for(i=0;i<n;i++)//输出矩阵
{
for(j=0;j<n;j++)
{
cout << setw(4) <<a[i][j];
}
cout << endl <<endl;
}
return 0;
}此处思路是大环套小环的“嵌套”思路,即由外圈向内,逐圈进行计算,得益于数组可以先计算再输出的所谓优点,可以先计算出每一圈各个位置的每个数之后,再进行整体的输出。这里的方法更将每一环切分为4小段,再对每一段上的每一个数进行填充。
二.循环输出法
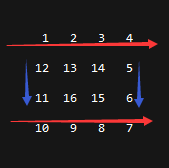
这种方法是最原始的方法,就是将矩阵的每环由外至内循环输出,最外层的为0环,环数向内依次递增。每环的数据分段输出,分段规则如下图所示,这里以6阶矩阵的0环为例。
依次输出红框中的数据——>绿框中的数据——>蓝框中的数据——>黄框中的数据,每个框中数据输出的顺序是从上到下,从左到右。
#include <iostream>
#include <iomanip>
#define max(a,b) (((a) > (b)) ? (a) : (b))
#define min(a,b) (((a) < (b)) ? (a) : (b))
using namespace std;
int matrix(int i, int j, int n);
int main()
{
int n, i, j;
cout << "Please input N:";
cin >> n;
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
cout << setw(4) << matrix(i, j, n);
}
cout << endl <<endl;
}
return 0;
}
int matrix(int i, int j, int n)
{
int m, a, l;
//计算在第几环,每环相当于一个子空心矩阵
m = min( min( i, n-1-i ), min( j, n-1-j ) );
//让每一个子矩阵的首元素的下标都为[0][0],这样所有的子矩阵就可以同等对待
i -= m;
j -= m;
a = 1 + 4*m*(n-m); //首元素
l = n - 2*m; //环边长
if (i == 0)
{
//返回红框中的元素。
return a+j;
}
else if (j == 0)
{
//返回绿框中的元素。以0环为例,0环的元素个数为6*4-4=(6-1)*4,
//即0环矩阵每条边的元素(边长)*边数-四个被重复计算了的元素。
//很显然元素20=1+4*(6-1)-1,19=1+4*(6-1)-2,......
//绿框中的元素随着行数增加而递减,于是得出如下规律。
return a + 4*(l-1) - i;
}
else if (i == l-1)
{
//返回蓝框中的元素。元素15等于0环的最大元素a+4*(l-1)-1减去5(即l-1),
//也就是15=a+4*(l-1)-1-(l-1)=a+3*l-4=a+3*l-3-j,对于15而言,j=1。
return a + 3*l - 3- j;
}
else if (j == l-1)
{
//返回黄框中的元素。
return a + l-1 + i;
}
}
三.任意阶矩阵
既然是任意阶矩阵,那么N阶矩阵当然包括在内,强烈推荐这种写法。
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
int n=6,m=6;
cout << "Please input M:";
cin >> m;
cout << "Please input N:";
cin >> n;
int num[100][100]={0};
int count = 1;
int x = 0, y = 0;
int dx = 0, dy = 1;
while (count <= m * n)
{
num[x][y] = count;
x += dx;
y += dy;
if (dy == 1 && (y >= n - 1 || num[x][y+1] != 0))
{
dx = 1;
dy = 0;
}
else if (dx == 1 && (x >= m - 1 || num[x+1][y] != 0))
{
dx = 0;
dy = -1;
}
else if (dy == -1 && (y <= 0 || num[x][y-1] != 0))
{
dx = -1;
dy = 0;
}
else if (dx == -1 && (x <= 0 || num[x-1][y] != 0))
{
dx = 0;
dy = 1;
}
count++;
}
for(int i=0;i<m;i++)//输出矩阵
{
for(int j=0;j<n;j++)
{
cout << setw(4) <<num[i][j];
}
cout << endl <<endl;
}
return 0;
}输出结果,7*9阶矩阵
四.变种
最近去快手面试,碰到了一个螺旋矩阵的变种,要求是这样的:给出一个正常的M*N阶数字矩阵,螺旋输出。
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
即输出结果为:1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10
对于这道变形题,只需要将上面的代码稍作修改即可,将二位数组的赋值改为输出,代码如下。
#include <iostream>
#include <iomanip>
using namespace std;
const int size = 4;
int num[size][size] = {
1, 2, 3, 4,
5, 6, 7, 8,
9, 10, 11, 12,
13, 14, 15, 16
};
int main()
{
int n=4,m=4;
int count = 1;
int x = 0, y = 0;
int dx = 0, dy = 1;
for(int i=0;i<m;i++)//输出矩阵
{
for(int j=0;j<n;j++)
{
cout << setw(4) <<num[i][j];
}
cout << endl <<endl;
}
while (count <= m * n)
{
cout<< num[x][y] << " ";
num[x][y]=0;
x += dx;
y += dy;
if (dy == 1 && (y >= n - 1 || num[x][y+1] == 0))
{
dx = 1;
dy = 0;
}
else if (dx == 1 && (x >= m - 1 || num[x+1][y] == 0))
{
dx = 0;
dy = -1;
}
else if (dy == -1 && (y <= 0 || num[x][y-1] == 0))
{
dx = -1;
dy = 0;
}
else if (dx == -1 && (x <= 0 || num[x-1][y] == 0))
{
dx = 0;
dy = 1;
}
count++;
}
cout<<endl;
return 0;
}参考链接:https://blog.csdn.net/pre_waist_l/article/details/79755293
参考链接:https://blog.csdn.net/dongsh315/article/details/24377191



























 229
229











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










