本文提供的复习题来自一所高校的全日制研究生的高等工程数学的往年期末考试真题,使用教材为《高等工程数学》张韵华版,考试范围仅该书前十章(矩阵论和数值计算)。每道题目给出的答案不一定正确,有部分答案写的不够详细,仅供参考。
答案勘误:
- 修改了计算题第一题的答案;
- 修改了填空题第四题;
- 补充了一下计算题第二题;
- 修改了并解释了填空题第三题;
- 修改了第二大题的计算题第四题的题目和答案。
课程名称 高等工程数学 拟题老师签名 教研室主任签名
课程编号 适应年级 工科研一 2020 至 2021 学年 一 学期 考核方式 考试
| 一、填空题(每小题4分,共20分) 1、对二阶方阵A做初等行变换
2、设A,B为2阶方阵,已知|A|=-1,|B|=2,则
3、向量
4、设A=
5、矩阵A= 二、计算题(每小题10分,共60分) 1、设
变换到
求线性变换A在基
2、构造求解方程组
原因:变换后其系数矩阵严格对角占优,所以GS迭代收敛。 (注:本题也可从迭代矩阵判断是否收敛) 3、求一个次数不超过3的多项式
并写出其余项的表达式。
4、用逐次分半的复化梯形公式计算积分
5、用向前和向后Euler公式解初值问题(取h=0.1)
6、用Newton法求
三、简答题(每小题10分,共20分) 1、设非齐次线性方程组
2.(1)简述用最小二乘法构造拟合曲线的原理。
基本原理:所有数据点与估计点(或称拟合点)的误差(如果是二维图形误差就是数据点与估计点的垂直距离)的平方和。如果所拟合的曲线能使该误差平方和最小,这就得到最小二乘法拟合曲线。
(2)按最小二乘原理,求解下列矛盾方程组:
|








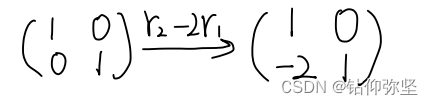





 ,则
,则 =_________
=_________

 的Doolittle分解式为
的Doolittle分解式为 


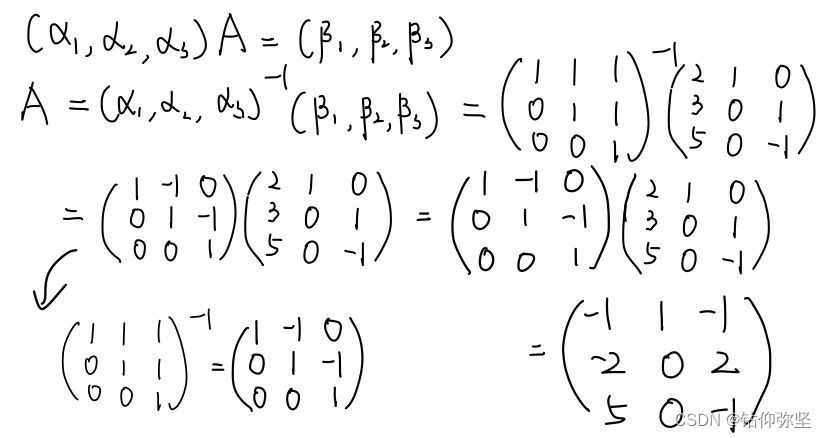
 ,必收敛的Gauss-Seidel迭代格式,并说明收敛的理由。
,必收敛的Gauss-Seidel迭代格式,并说明收敛的理由。
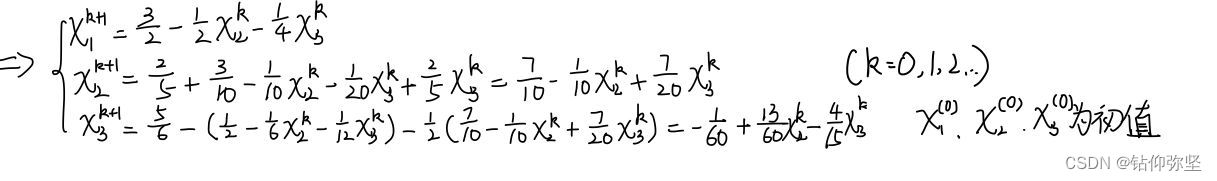
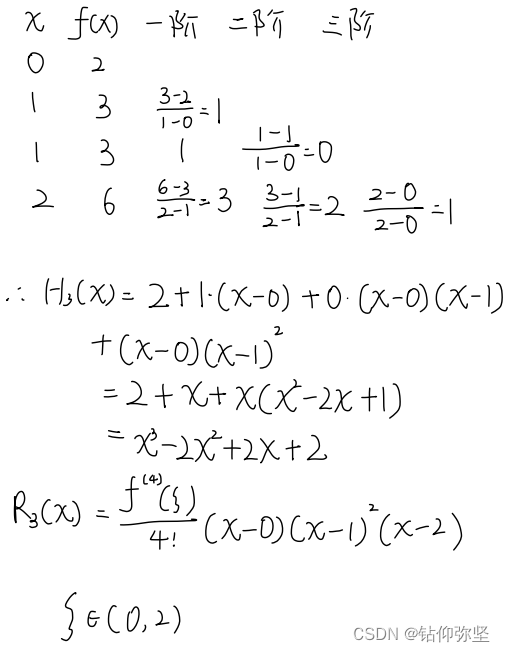






 线性无关。
线性无关。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










