高等工程数学第6-10章大题总结（数值计算）

本篇主要总结了高等工程数学张韵华版第6-10章，即数值计算部分的重点大题题型。答案仅供参考。

第六章

一、Gauss列主元消元法

1.用列主元消元法解方程组：

二、矩阵的Crout分解和Doolittle分解

1.用 Doolittle（即 LU）分解法求解如下线性方程组:

2.用Crout分解法求解下列线性方程组。

3.矩阵的Doolittle分解式为

答案：

4.矩阵的Crout分解式为

答案：

三、Jacobi迭代格式及其收敛性

对于方程组 AX = y，构造雅可比迭代式。当迭代矩阵B的谱半径P<1时，迭代收敛，这是收敛的充要条件.迭代矩阵的某范数||B||<1，是迭代收敛的充分条件。当方程组的系数矩阵 A 具有某些特殊性质时，可直接判定由它生成的雅可比迭代矩阵是收敛的.
定理6.1 若方程组AX = y的系数矩阵A 满足下列条件之一，则其雅可比迭代收敛：

1.设线性代数方程组Ax=b的系数矩阵为

试求能使Jacobi方法收敛的a的取值范围。

2.设线性代数方程组Ax=b的系数矩阵为

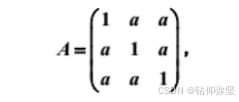
其中a为实数，试求能使Jacobi方法收敛的a的取值范围。

四、Gauss-Seidel的迭代格式及其收敛性

判断Gauss-Seidel迭代收敛与判断雅可比迭代收敛的方法类似。一方面从Gauss-Seidel迭代矩阵S获取信息，当p(s)<1或S的某种范数||S||<1时，Gauss-Seidel迭代收敛;另一方面，有时可直接根据方程组系数矩阵的特点做岀判断。
定理6.2 若方程组系数矩阵为列或行严格对角优的，则Gauss-Seidel迭代收敛。
定理6.3 若方程组系数矩阵为对称正定矩阵，则Gauss-Seidel迭代收敛。

1.构造收敛的Gauss- Seidel 迭代格式（不计算），并说明收敛的理由。

2.构造收敛的 Gauss-Seidel 迭代格式（不计算），并说明收敛的理由。

3.构造求解下列方程组必收敛的 Gauss-Seidel 迭代格式，并说明收敛的理由。 

4.构造求解下列方程组必收敛的 GS 迭代格式，并说明收敛的理由。

第七章

一、Lagrange插值多项式（三次），误差余项

1.已知的函数表如下，利用二次Lagrange插值多项式求的近似值，并估计误差。

 2.已知sin(x)的函数表如下，用二次Lagrange插值多项式，求sin0.63891的值，并估计误差。 

二、Newton插值多项式（三次），误差余项

1.设, 则其七阶差商

2.设 f(-1) = 0, f(0) = 1, f(1) = -2 ，则过这三点的二次插值多项式中  的系数为

答案：-2

三、Hermite插值多项式（三次），误差余项

1.求一个次数不超过 3 的多项式，满足下列插值条件：

并写出其余项的表达式。

方法一：

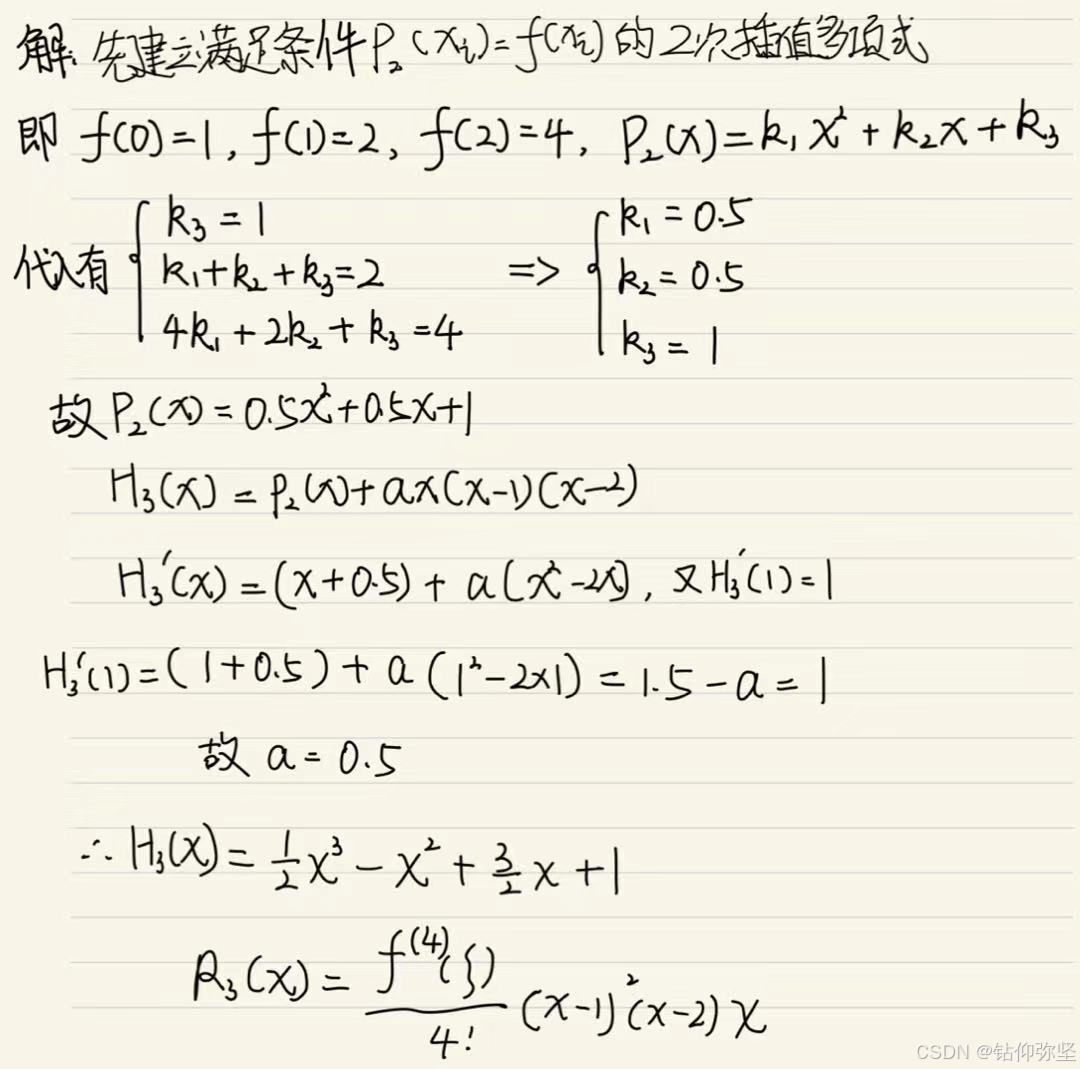
方法二：推广Newton插值法

2.给定数据f(0)=1,f'(0)=0.5,f(1)=2,f'(1)=0.5。构造一个次数不超过3次的多项式H(x)，计算 f(0.5)的近似值，并写出余项f(x)-H(x)的表达式。

四、最小二乘法原理，一次多项式（线性）拟合

1.设有实验数据

按最小二乘法求一次多项式进行拟合。

五、按最小二乘原理解矛盾方程组

 1.按最小二乘原理，求解下列矛盾方程组:

2.按最小二乘原理，求解下列矛盾方程组:

第8章 数值微分和数值积分

一、求积公式的代数精度

1.求积公式，具有_____次代数精度。

答案：1

2.n个结点的插值型求积公式至少具有_______次代数精度，n 个结点的Gauss型求积公式具有_______次代数精度。

答案：n-1 ; 2n-1

有的题目问的是n+1个结点，注意别搞混了。

3.中矩形求积公式的代数精度为______次，截断误差为_______( f(x) 充分光滑)

答案：1    

本题第二空是高等工程数学张韵华版教材185页第二题第二问。

此外，常见的求积公式中，左矩形、右矩形求积公式的代数精度为0；梯形公式的代数精度为1（这是高等工程数学张韵华版第一版教材168页的原话）。

4.牛顿-科茨数值求积公式,当n为奇数时,至少____次代数精度;当n为偶数时,至少具有____次代数精度.
答案：n  ;  n+1

这是高等工程数学张韵华版第一版教材169页的原话。

5.n个结点的所有求积公式中，具有最高代数精度的是________求积公式。

答案：Gauss型

6. 求积公式，具有_____次代数精度。

答案：3

二、插值型求积公式：梯形公式和辛普森公式

1.分别用梯形公式和Simpson公式计算积分的近似值，并估计截断误差。

2.分别用梯形公式和Simpson公式计算积分的近似值，并估计梯形公式的截断误差。

三、复化梯形公式和复化辛普森公式

1.用复化梯形公式计算，使其截断误差不超过0.01。

2.给定定积分

(1)利用复化梯形公式计算上述积分值，使其截断误差不超过0.5×。

(2)取同样的求积节点，改用复化辛普森公式时，截断误差是多少？

(3)要求截断误差不超过,若用复化辛普森公式，应取多少个函数值？

(4)利用复化辛普森公式计算上述积分值，使其截断误差不超过0.5×。

四、区间逐次分半的复化梯形公式

1.用逐次分半的复化梯形公式计算，使截断误差不超过0.005。

2.用逐次分半的复化梯形公式计算，使截断误差不超过。

3.用逐次分半的复化梯形公式计算，使其截断误差不超过0.01。

第9章 常微分方程数值解

一、显式欧拉法

1.试写出用 Euler 法求解初值问题：

的计算公式，取步长 h =  0.1 ，写出计算结果。

2.用Euler方法求解常微分方程初值问题

的计算公式为____________，其中 h = 0.1 。

3.用Euler方法求解常微分方程初值问题

的计算公式为____________，其中 h = 0.1 。

第10章 迭代法

一、简单迭代法及其收敛性

1.证明方程在[0，0.5]上有唯一正根和迭代

对任意初值[0，0.5]收敛。

二、Newton法及其收敛性

1.写出求方程的根的Newton迭代格式，并说明收敛理由。

(这道题方程的根约为1.715621)

2.写出计算 (a>0) 的 Newton 迭代格式，用它求 的近似值（计算一步求出 即
可），并说明收敛的理由。

3.用Newton法求非线性方程 x+sinx=1的根(计算一步求出 即可)，并说明收敛的理由。

4.取s=0.01，用 Newton法求方程

在附近的根。

5.给定方程,
1)证明方程在区间(1,2)内仅有一个根;
2)写出求方程在区间(1,2)内根的 Newton 法迭代公式，并说明收敛的理由。