感应电机MTPA控制变分法优化

一种用于电动汽车续航优化的感应电机 最大转矩每安培控制的变分方法

摘要

本文提出了一种感应电机控制策略，可在瞬态和稳态下同时优化效率和转矩响应。在感应电机矢量控制的框架内，针对参考转矩的阶跃变化，基于变分法定义了最优问题。由此可求得使定子电流幅值最小化的电流参考轨迹的解析闭式解。仿真与实验结果验证了该方法的有效性，表明驱动效率得到了显著提升。因此，若将感应电机应用于电动汽车动力总成中，所提出的控制策略可提高单次充电续航里程，案例分析的结果证实了这一点。

索引词 —电动汽车，感应电机，矢量控制，最大转矩每安培控制，变分法。

符号表

• iss 定子坐标系中的定子电流空间矢量
• ismr 在定子坐标系中表示转子磁通的励磁电流空间矢量
• isd , isq 定子电流空间矢量在转子磁通坐标系下的分量
• j 虚数单位
• p 极对数
• ps 瞬时定子功率损耗
• t 时间
• ωr 电机转速
• Lm 励磁电感
• L′r 折算到定子侧的总转子电感
• T 电磁转矩
• Tr 转子时间常数
• Ws 定子能量损耗

I. 引言

在电动汽车中，单次充电续航里程是需要关注的主要问题之一。它是指电动汽车电池充满电后的行驶距离。对于给定的电池组，通过提高动力总成效率可增加单次充电续航里程。然而，由于效率会随使用条件的变化而变化，通常基于标准化的统一驾驶循环（如全球统一轻型车辆测试程序（WLTP）[1]）来确定。为了准确模拟车辆的不同运行条件，所有标准驾驶循环的一个共同特点是：车辆动力总成所需的扭矩曲线在幅值和频率上均会受到较大变化的影响。这意味着动力总成的运行条件经常处于动态状态，远离额定状态。因此，考虑稳态效率没有意义，而瞬态效率更为重要。

电动汽车动力总成通常采用感应电机，因其具有高可靠性、坚固性和低成本。此外，当前对这类电机重新关注，原因在于政治和经济不稳定可能导致稀土元素供应困难，从而影响永磁同步电机的应用。

感应电机驱动的最优稳态效率控制已受到研究员的广泛研究 [2],[3],[4]。如果需要对电磁转矩实现快速精确控制，可以采用经典磁场定向控制 [5],[6]，但其缺点是在轻载条件下仍以额定磁通运行，因此在低电磁转矩值时效率可能很低。一种有前景的方法是最大转矩每安培（MTPA）控制策略[7]，但所提出的解决方案仅在稳态运行条件下保证给定负载转矩下定子电流幅值的最小化。

在[8]中，磁场定向控制策略与同步旋转坐标系上的解耦控制及最大转矩每安培控制策略相结合。在[9]中，通过基于感应电机损耗模型的在线损耗最小化算法来确定用于效率优化的磁通水平，其主要缺点是对电机参数的依赖性。

在[10]中，最大转矩每安培控制策略被用于感应电机的矢量控制，但通过引入转矩电流补偿进行了改进，以削弱由于转子磁通变化引起的转矩动态性能恶化。在[11]中提出了一种控制算法，该算法根据瞬态或稳态运行情况采用两阶段控制。

一些研究尝试解决感应电机在瞬态过程中运行优化的问题。其中大多数采用了最优控制理论。在[12]中，使用动态规划方法来求解d轴和q轴电流的给定值。

将分量作为控制输入以最小化瞬态能量损耗。该控制策略基于贝尔曼方程的离线数值解，需要预先知道负载转矩。结果被存储在控制器中的查找表中。其他研究 [13],[14],[15]使用庞特里亚金最小值原理来获得最大转矩每安培输入，但同样仅给出了离线数值解，并通过查找表进行控制。

由于该问题的适当数学表述在于寻找使给定泛函最小化的函数，因此可将其视为变分法中的经典问题，如[16]和[17]所示。然而，前者未提供仿真或实验结果，而后者在转矩瞬态过程中假设速度恒定，且仅给出了近似解。

本文的贡献在于采用变分法，求解在给定参考转矩阶跃变化条件下，为最小化定子电流幅值而优化感应电机矢量控制中参考电流分量时间轨迹的问题，并获得其解析闭式解。仿真与实验结果验证了所提出控制策略的可行性与有效性。

本文的其余部分组织如下。第二部分简要回顾了感应电机驱动的磁场定向控制和最大转矩每安培控制策略。第三部分通过使用变分法，将优化问题表述为泛函最小化问题，并给出了解析闭式解。第四部分描述了所提出方案的仿真与实验验证，并将其与磁场定向控制和最大转矩每安培控制策略进行了比较。第五部分是一个案例分析，研究了将所提出的控制策略应用于实际电动汽车在WLTP驾驶循环下的性能表现。最后，第六部分给出了结论。

II. 背景

在经典的磁场定向控制[5],[6]中，通过假设定子电流由快速电流控制环路作用而施加，来分析感应电机的动态行为。这样可以得到显著简化，因为只需考虑转子方程，其可表示为：

$$
T_r \frac{di_{smr}}{dt} + (1 - jp\omega_r T_r) i_{smr} = i_{ss}
$$

其中，$i_{smr}$、$i_{ss}$ 分别为定子坐标系下表示转子磁通的定子电流和励磁电流的空间矢量，$p$、$\omega_r$、$T_r$分别为极对数、电机转速和转子时间常数。

如果 $i_{mr}$ 和 $\rho$ 分别表示 $i_{smr}$ 的幅值和相位角，即：

$$
i_{smr} = i_{mr} e^{j\rho}
$$

复方程(1)可以分解为实部和虚部：

$$
\begin{cases}
T_r \frac{dimr}{dt} + imr = isd \
\frac{d\rho}{dt} = p\omega_r + \frac{isq}{Trimr}
\end{cases}
$$

其中

$$
isd + j isq = iss e^{-j\rho}
$$

表示在由空间矢量 $i_{smr}$ 定义的转子磁通坐标中的定子电流矢量，转子磁通 $\phi_r$ 由以下给出

$$
\phi_r = L’ r i {mr}
$$

其中 $L’_r$ 表示折算到定子侧的总转子电感，而电磁转矩 $T$ 可表示为

$$
T = k_t i_{mr} i_{sq} \quad \text{with} \quad k_t = \frac{3pL_m^2}{2L’_r}
$$

其中 $L_m$ 是励磁电感。

从期望转矩、估计磁通和转速的测量值出发，控制算法必须提供d-q轴电流分量的参考值，如图1所示。由于转矩的瞬时值不依赖于 $isd$ 的瞬时值，因此控制算法具有一个可利用的自由度。

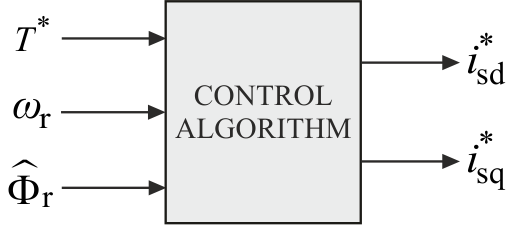
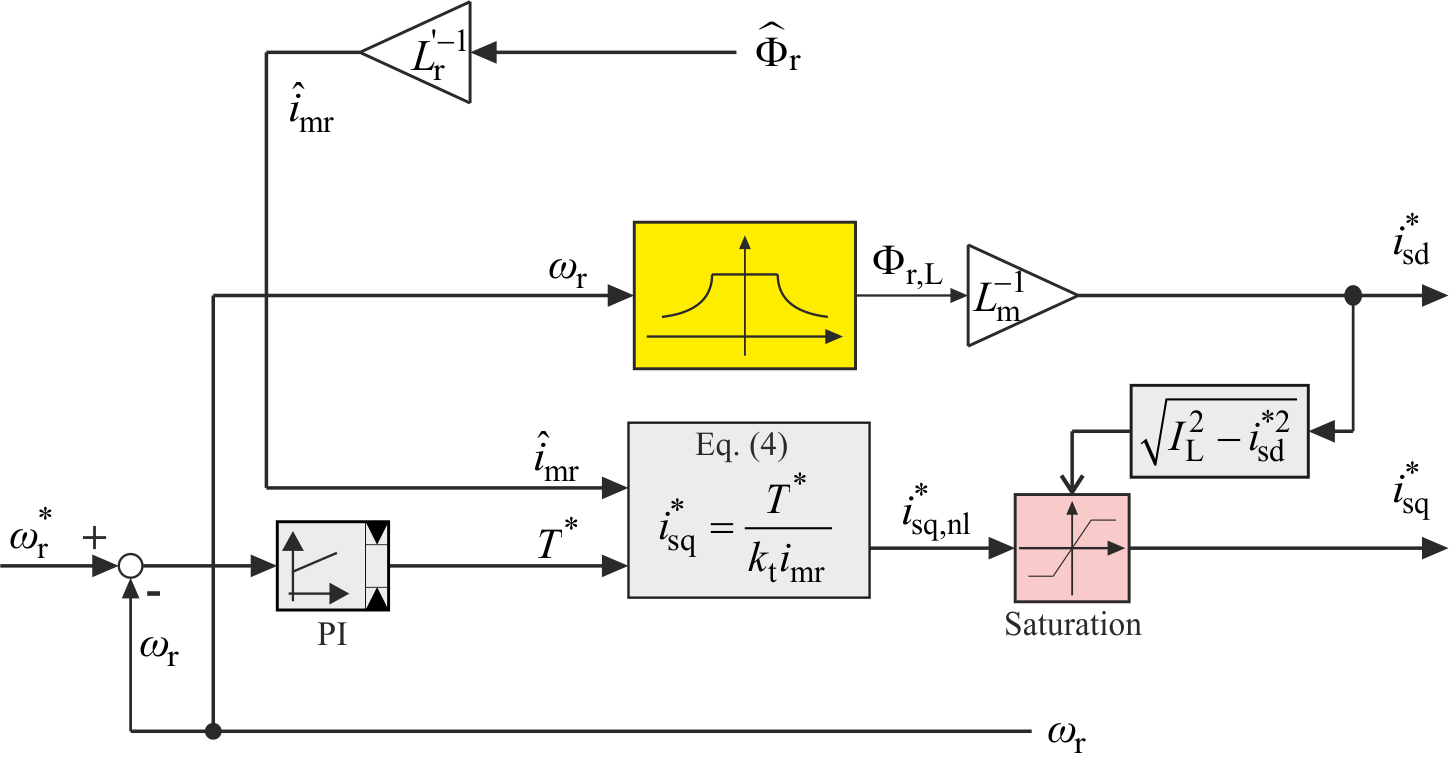
传统磁场定向控制策略（用TF表示）通过固定 $i^ _{sd}$，根据众所周知的磁通-速度定律实现最大磁通，即在恒转矩区（基速以下）保持恒定，在恒功率区（基速以上）呈双曲线下降。由于机械时间常数通常远大于 $T_r$，可假设 $i^ {sd} = i {mr}$。TF策略框图如图2所示，其中黄色高亮部分表示TF策略如何在 $i^*_{sd}$ 上固定自由度。

如图所示，(4) 给出了 $i^ _{sq}$ 的非限值（用 $i^ _{sq,nl}$ 表示）。由于电机电流限制，该值随后被限制以获得

$$
i^2_{sd} + i^2_{sq} \leq I^2_L
$$

其中 $I_L$ 表示电机电流限值。该策略通过控制定子q轴电流分量，实现对电磁转矩的快速精确控制。特别是，由于磁通始终维持在最大值，因此在转矩-速度运行区域内可瞬时产生任意 $T^ $ 值。另一方面，即使在 $T^ $ 值较低的情况下，电机也始终在最大磁通下运行，并且 $i_{sd}$ 处于最大值，从而导致效率下降。

在稳态下，该问题可以通过最大转矩每安培控制策略 [7] 来解决。事实上，根据(2)的第一式，在稳态下有 $i_{mr} = i_{sd}$。因此，稳态输出转矩可以表示为

$$
T = k_t i_{sd} i_{sq}
$$

因此，在稳态下，为了在给定转矩下获得定子电流最小幅值，控制策略必须施加

$$
i^ _{sd} = i^ _{sq} = \sqrt{\frac{T^*}{k_t}}
$$

其中上标 * 表示参考值。显然，在瞬态运行中，由于d轴电流分量 $i_{sd}$ 的变化以及根据(2)式中的第一个关系式存在的 $i_{sd}$ 与 $i_{mr}$ 之间的一阶延迟，该控制策略将导致输出转矩动态性能下降。

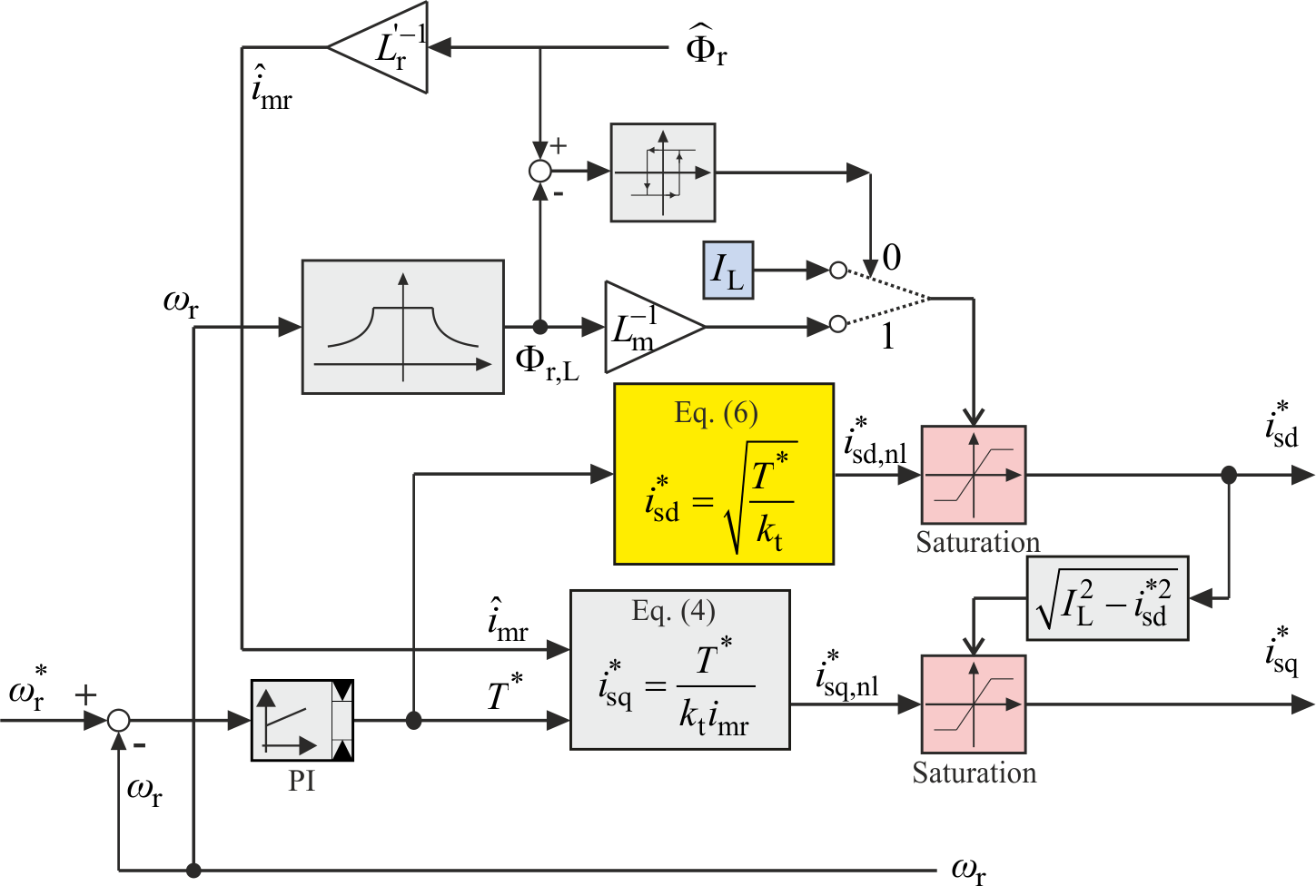
为了提高转矩动态性能，当 $i^ _{sd}$ 根据(6)计算时，$i^ {sq}$ 可根据转子磁链的实际值按照(4)进行设定。由此得到传统每安培最大转矩策略（记为TM）[10]。图3显示了相应的框图，其中以黄色突出显示的模块表示TM策略如何确定 $i^ _{sd}$ 的自由度。可以看出，(6)提供了 $i^ {sd,nl}$ 的非限幅值（记为 $i^ _{sd,nl}$）。实际上，对于当 $T^ $ 取高值时，根据(6)确定的d轴电流可能导致电机铁芯饱和。因此，如果估计的转子磁链超过由磁通-速度定律给出的极限值 $\phi_{r,L}$，则必须将d轴电流分量限制在 $\phi_{r,L}/L_m$。在图3中，将估计的转子磁链与极限值 $\phi_{r,L}$ 进行了比较。其差值随后由滞环调节器处理，从而实现对 $i^ {sd,nl}$ 的限制。如果估计的转子磁链未超过其极限值，则与传统磁场定向控制（TF）策略类似，需限制d轴电流以获得 $i^2 {sd} + i^2_{sq} \leq I^2_L$。由于存在电流和电压限制，并非所有的转矩阶跃变化都能瞬时产生。例如，若要求从 $T^ 0$ 到 $T^ _1$ 发生 $T^ $ 阶跃变化，且 $T^ _0$ 过低，系统将从转子磁链低值开始运行，导致产生 $T^ _1$ 所需的q轴电流高于 $I_L$ 而无法施加。随着磁通按转子时间常数 $T_r$ 逐渐增加，最终能够满足所要求的 $T^ _1$ 值。无论如何，通过(6)设定 $i^ {sd}$ 以及通过(4)设定 $i^*_{sq}$ 仅能在稳态条件下保证最大转矩每安培运行。

下一节提出了允许将最大转矩每安培控制策略扩展到暂态运行的解析解。

III. 变分方法

A. 问题设定

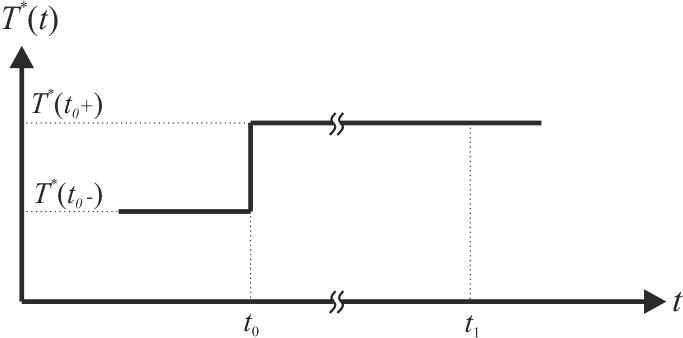
给定如图4所示的转矩需求 $T^*(t)$ 的阶跃变化，从数学角度来看，目标是找到时间函数 $i_{sd}(t)$ 和 $i_{sq}(t)$，使其既能满足转矩需求，又能最小化积分

$$
\int_{t_0}^{t_1} [i^2_{sd}(t) + i^2_{sq}(t)] dt
$$

其中 $t_0$ 和 $t_1$ 是对应于稳态运行条件的两个时间点，在该条件下，d轴和q轴电流分量根据最大转矩每安培控制策略确定，

$$
\begin{cases}
i_{sd}(t_0^-) = i_{sq}(t_0^-) = \sqrt{\frac{T^ (t_0^-)}{k_t}} \
i_{sd}(t_1) = i_{sq}(t_1) = \sqrt{\frac{T^ (t_0^+)}{k_t}}
\end{cases}
$$

对于任意时间函数 $i_{sd}(t)$，(2) 式的第一个方程的解为 [18]

$$
i_{mr}(t) = \frac{1}{T_r} e^{-t/T_r} \int_{t_0}^{t} i_{sd}(\tau) e^{\tau/T_r} d\tau + i_{mr}(t_0) e^{-t/T_r}, \quad t \geq t_0
$$

因此，为了满足转矩需求，q轴电流分量由以下给出

$$
i_{sq}(t) = \frac{T^ (t)}{k_t i_{mr}(t)} = \frac{T^ (t)}{k_t \left[ \frac{1}{T_r} e^{-t/T_r} \int_{t_0}^{t} i_{sd}(\tau) e^{\tau/T_r} d\tau + i_{mr}(t_0) e^{-t/T_r} \right]}
$$

变换

$$
y(t) = \int_{t_0}^{t} i_{sd}(\tau) e^{\tau/T_r} d\tau \Rightarrow y’(t) = i_{sd}(t) e^{t/T_r}
$$

允许将积分(7)写成泛函

$$
J[y] = \int_{t_0}^{t_1} F[y(t), y’(t), t] dt
$$

with

$$
F[y(t), y’(t), t] = \frac{T^{*2}(t)}{k_t^2} e^{-2t/T_r} \left[ \frac{1}{T_r} y(t) + i_{mr}(t_0) \right]^2 + y’^2(t) e^{-2t/T_r}
$$

通过这种方式，寻找满足转矩需求并使积分(7)最小化的时间函数 $i_{sd}(t)$ 和 $i_{sq}(t)$ 的问题，被转化为寻找使泛函(12)取得极小值的函数 $y(t)$ 的问题，即转化为一个经典的变分法问题。泛函(12)存在极大值或极小值的必要条件由欧拉-拉格朗日方程[19]给出。

$$
\frac{\partial F}{\partial y} - \frac{d}{dt} \left( \frac{\partial F}{\partial y’} \right) = 0
$$

在所考虑的情况下，式(14)得出

$$
\frac{T^{*2}}{k_t^2 T_r} e^{-2t/T_r} \left[ \frac{1}{T_r} y(t) + i_{mr}(t_0) \right]^3 + e^{-2t/T_r} \left[ y’‘(t) - \frac{2}{T_r} y’(t) \right] = 0
$$

其中 $T^ (t) = \text{constant} = T^ (t_0^+) = T^*$ 假设成立。

B. 提出的解决方案

微分方程(15)可以通过设置来求解

$$
i_{sd}(t) = i_{sq}(t)
$$

这样，由(10)和(11)可得

$$
\frac{1}{T_r} y(t) + i_{mr}(t_0) = \frac{T^*}{k_t} y’(t) e^{2t/T_r}
$$

并将(17)代入(15)

$$
y’‘(t) - \frac{2}{T_r} y’(t) = -\frac{k_t}{T_r T^*} y’^3(t) e^{-2t/T_r}
$$

考虑到(11)，式(18)变为

$$
i’ {sd}(t) = \frac{1}{T_r} i {sd}(t) - \frac{k_t}{T_r T^*} i^3_{sd}(t)
$$

这是一个伯努利微分方程。如果引入 $z(t) = i^{-2}_{sd}(t)$，它就简化为线性方程

$$
z’(t) + \frac{2}{T_r} z(t) - \frac{2k_t}{T_r T^*} = 0
$$

初始条件

$$
i_{mr}(t_0^-) = i_{mr}(t_0^+) = i_{sd}(t_0^-)
$$

最终，结合(4)和(16)可得

$$
i_{sd}(t) = i_{sq}(t) = \frac{1}{\sqrt{ \left[ \frac{k_t T^ (t_0^-)}{T^{ 2}} - \frac{k_t}{T^ } \right] e^{-2t/T_r} + \frac{k_t}{T^ } }}
$$

由于可以很容易地证明，由(13)式定义的函数 $F$ 关于 $y(t)$ 和 $y’(t)$ 是严格凸的，因此该泛函的最小值存在且唯一。因此，(21)式表示了在转矩需求发生阶跃变化时，使定子电流幅值最小的d轴和q轴电流分量的时间轨迹的闭式解析表达式。显然，它是

$$
\lim_{t \to +\infty} i_{sd}(t) = \lim_{t \to +\infty} i_{sq}(t) = \sqrt{\frac{T^*}{k_t}}
$$

这将得到(6)。需要强调的是，(21)与(6)有很大不同。实际上，(21)指的是瞬时的 $i_{sd}$ 和 $i_{sq}$ 值，而(6)仅适用于稳态运行。

所提出的动态MTPA策略（记为DM）的框图如图5所示，其中以黄色突出显示的节点表示DM策略如何根据式(16)在 $i^*_{sd}$ 上固定自由度。与TM情况类似，由于存在电流和电压限制，并非所有的阶跃变化都能由DM瞬时产生。然而，正如后续将阐明的，DM的动态性能优于TM。

IV. 仿真与实验分析

为了清晰起见，在以下图示中，上述三种控制策略各自唯一地关联了一种颜色：
- 传统磁场定向控制（TF） - 红色
- 传统最大转矩每安培（TM） - 绿色
- 动态最大转矩每安培策略（DM） - 蓝色
DM是本文提出的方法。

已对所提出方法可实现的性能进行了初步定性分析。在参考转矩发生阶跃变化时，根据DM策略，$i_{sd}$和$i_{sq}$的定性行为如图6.a所示。图6.b显示了采用TF策略得到的相同电流分量。瞬时定子功率损耗$p_s$：

$$
p_s = \frac{3}{2} R_s(i^2_{sd} + i^2_{sq})
$$

如图6.c所示，针对两种控制策略的定子能量损耗情况。正如预期，传统磁场定向控制（TF）具有较高的定子能量损耗$W_s$（图6.d）。$W_s$(DM)与$W_s$(TF)之间的显著差异主要源于转矩参考值阶跃变化前后较长的稳态持续时间。在相同的参考转矩阶跃变化下，根据传统最大转矩每安培（TM）策略，$i_{sd}$和$i_{sq}$的定性行为如图7.a所示。图7.b比较了TM和DM的瞬时定子功率损耗。尽管在阶跃变化时刻$p_s$(DM)可能高于$p_s$(TM)，但DM更高的$i_{sd}(t)$使其能够快速增加转子磁通，从而只需较小的$i_{sq}(t)$即可满足期望转矩要求。因此，$p_s$(DM)迅速降至$p_s$(TM)以下，最终使得定子能量损耗$W_s$(DM)低于$W_s$(TM)，如图8所示。

此外，在存在电压和电流限制的情况下，DM表现出更优的转矩响应。图9展示了当需要转矩阶跃变化但无法立即实现时，TM与DM之间的对比。从图9.a可以看出，TM方法将$i_{sd}$直接设为新的稳态值，且无电流限制。发生这种情况时，相应的磁通根据$T_r$时间常数增加（图9.c）。另一方面，由于请求的q轴电流高于电机电流限值，$i_{sq}$被限制为$\sqrt{I_L^2 - i^2_{sd}}$（图9.b），因此初始输出转矩（图9.d）低于$T^ $。随着磁通的增加，转矩达到$T^ $。而对于DM（图9.d），由于其设置为$i_{sd} = i_{sq}$，电流限制同时作用于两个电流分量，导致产生的初始转矩更低。然而，由于具有更高的$i_{sd}$值，磁通增加得更快，从而使转矩上升也更迅速。此外，当磁通达到其限值$\phi_{r,L}$时，滞环调节器（图5）启用对$i_{sd}$的限制，将其限制为$\phi_{r,L}/L_m$。因此，$i_{sq}$可以跃升至$\sqrt{I_L^2 - (\phi_{r,L}/L_m)^2}$，使产生的转矩跃升至其最终值。DM的转矩稳定时间明显低于TM，且DM转矩的时间积分大于TM。

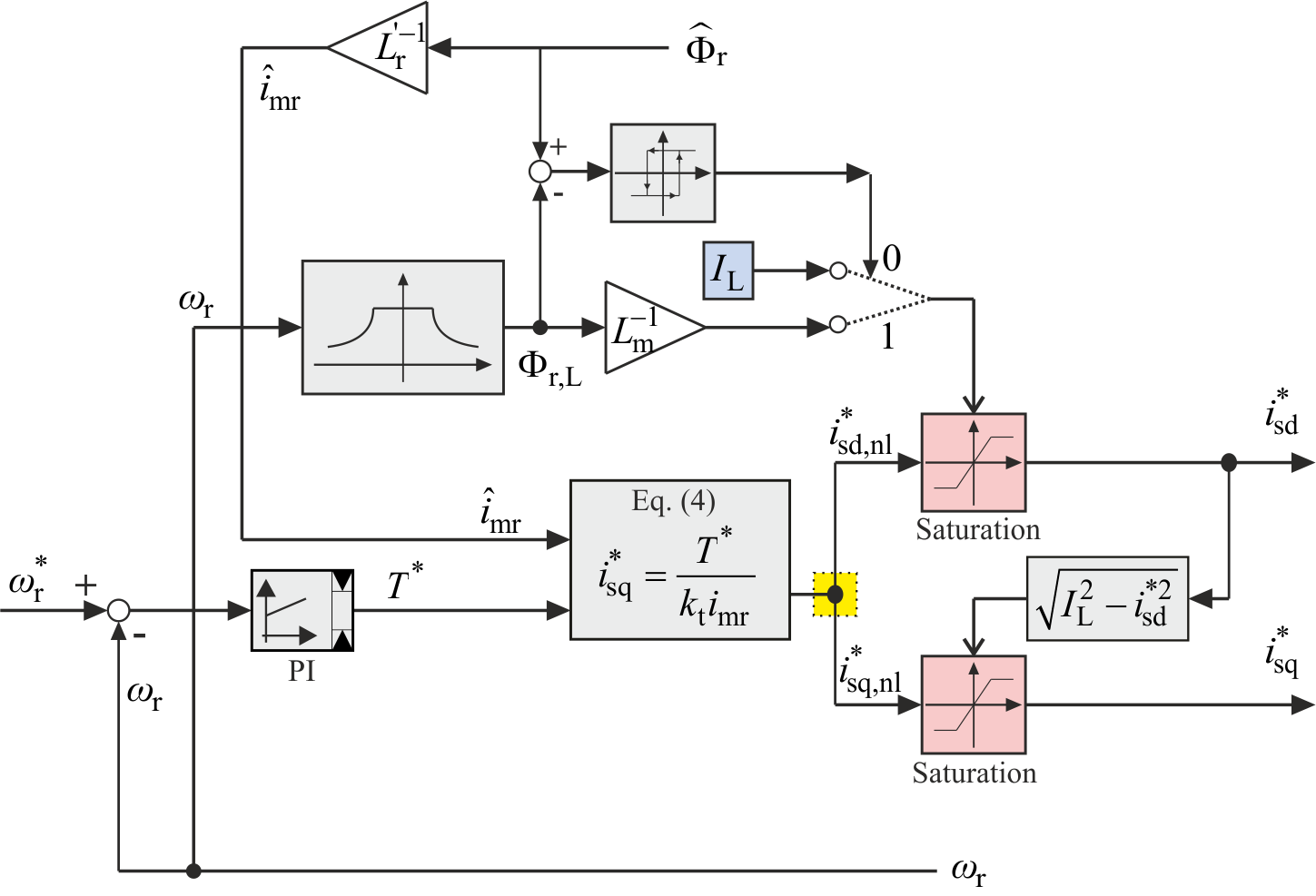
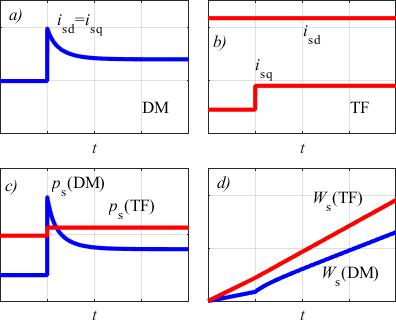
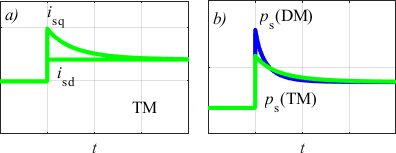
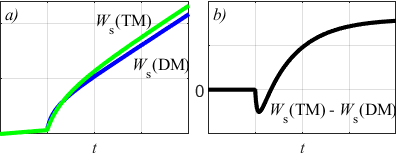
图10：试验台架设置。

为了验证定性分析，搭建了一个试验平台，将一台1.1千瓦感应电机与动态可控制动器连接（图10）。该电机由基于三菱PM100DSA120智能功率模块的标准电压源逆变器驱动，以实现功率部分。不同的控制策略通过dSPACE®模块化系统的DS1006处理器板实现。该系统与基于Altera® CPL EPM7160SLC8410的对称空间矢量调制单元相连接。调制单元生成周期为200µ秒的同步信号，用于触发处理器中断控制任务。具体而言，在每个采样时间$T_s$内，控制单元计算出下个$T_s$中逆变器调制所需的调制模式，并通过DS4003数字输入输出板输出。DS3002和DS2004板分别用于采集来自速度传感器的数字信号和模拟信号。来自电流和电压传感器的数据。表I中总结了被测电机和控制系统主数据。

一项初步实验基于三角形速度曲线，将动态最大转矩每安培策略（DM）与传统最大转矩每安培（TM）进行了比较，该速度曲线导致方波输出转矩行为。制动器施加恒定负载转矩。实验结果如图11所示。可以看出，两种策略产生的转矩和速度行为相同。在d轴电流分量方面，TM呈现出方波波形，仅在转矩阶跃变化期间与DM的行为有所不同。由于两种方法对应的转子磁通略有差异，q轴电流分量也因此不同。定子损耗如图11.f所示，但仅存在微小差异。图11.g展示了图11.f在转矩上升时刻附近的局部放大图。如图所示，并结合之前的分析（图3.b），在转矩上升时刻，DM相关的定子损耗高于TM，但下降更快。显然，曲线$p_s$下方的面积在DM情况下更小。为了突出DM性能的优势，图11.h展示了两种策略的定子能量损耗之差$\Delta W_s = W_{s,TM} - W_{s,DM}$。可以看出，$\Delta W_s$在每次转矩变化时（无论是上升还是下降）均增加，而在转矩保持恒定的时间段内则保持不变。这证实了在稳态运行期间两种方法均可保证最大转矩每安培比，这是由于转子时间常数$T_r$较小所致，且稳态运行占主导地位；但在瞬态过程中，只有DM能够保证最小电流。

第二项实验基于简单的参考速度曲线，将传统磁场定向控制（TF）与所提出的DM进行比较，同时根据牵引应用需求，由制动器施加二次方律负载转矩。此外，为了验证数值分析环境，通过Matlab Simulink®仿真，在两种方法下施加相同的速度和扭矩曲线进行模拟。

实验结果如图12所示，背景为灰色，而图13显示了数值输出（白色背景）。图12和图13均表明，DM策略的特点是d轴电流较低，这导致转子磁通降低。因此，为了产生相同的转矩，q轴电流的绝对值更高。通过参考瞬时定子功率损耗$p_s$，可以明显看出所提出方法的优势，其显著降低，从而带来更低的定子能量损耗$W_s$。总瞬时吸收电机功率用$p_b$表示。如果忽略逆变器和机械损耗，则$p_b$等于电动汽车的电池组提供的功率，而$W_b$表示吸收的能量。显然，对于动态最大转矩每安培策略（DM），吸收的功率和能量更低，这不仅确保了定子损耗的最小化，而且由于在较低磁通值下运行，也有助于减少铁损。为了更好地评估所提出方法的优势，定义了以下节能指数：

$$
\Delta W_b = \frac{W_{b,TF} - W_{b,DM}}{W_{b,TF}}
$$

$\Delta W_b$的行为在图12和图13中均用黑线表示，达到约70%的最终值。尽管该结果证实了所提出方法的有效性，但其值主要与原型机的小额定功率相关，且需实际研究全尺寸汽车应用。由于数值输出与测试结果几乎完全一致，仿真环境得到验证，可对全尺寸案例分析进行数值分析。

V. 案例分析

作为案例分析，考虑了一款经济型汽车，其特性与2018款日产Leaf相似，但配备的动力总成基于一台感应电机，该感应电机等效于实际安装在该车型上的同步交流电机。表II列出了车辆主要数据和预期的感应电机参数。

数值研究根据全球统一轻型车辆测试程序（WLTP）驾驶循环进行。具体而言，根据所考虑车辆的功率/重量比，选择了3类测试循环；整个循环分为三部分：低速、中速和高速。图14第一行显示了车辆速度$v$，而相应的加速度$a$则在第二行中表示。为了验证所提出策略的有效性，采用传统TF控制作为对比：同样地，TF控制的电输出量用红线表示，而蓝色则代表所提出的DM策略。图14的第三、第四和第五行分别展示了d轴和q轴定子电流分量以及转子磁通幅值的时间变化特性。可以看出，在WLTP的低速段，TF控制将$\phi_r$保持在1标幺值，仅在一个短暂的时间区间内（对应于$v > 50$ km/h时）由于电压限制需要进行弱磁控制。事实上，$i_{sd}$等于其额定值，因此$i_{sq}$的时间变化特性与加速度相似。相反，所提出的策略通过设置$i_{sd} = i_{sq}$，使得$\phi_r$的值较低，大多数情况下对应着更低的$i_{sd}$值。而$i_{sq}$的绝对值则始终更高，以产生相同的转矩。得益于相同的坐标轴尺度，显然$i_{sq}$的增加被$i_{sd}$更显著的减小所补偿，从而导致定子电流更低电流幅值。

在中高速段，TF控制根据速度曲线显著削弱电机磁通。然而，进一步减小磁通仍有较大余地，如图中蓝色曲线所示的$\phi_r$行为所证明，即使在$i_{sq}$增加的情况下，仍可实现更低的定子电流幅值。两种控制方式产生的能量量如图15所示。第一行显示了由于焦耳效应在定子绕组中损耗的能量$W_s$。与传统TF控制相比，所提出的DM策略显著降低了该值。相反，在转子绕组中损耗的能量$W_r$（第二行）更高。实际上，q轴转子电流$i_{rq}$与q轴定子电流$i_{sq}$成正比，因此所提出策略中增大的$i_{sq}$导致了更高的$i_{rq}$。而d轴转子电流$i_{rd}$仅在磁通瞬态期间存在，在恒定磁通时为零。考虑到所提出的策略在WLTP循环期间引入了更显著的磁通变化，因此$i_{rd}$也高于传统TF控制。因此，所提出的策略具有更高的转子电流幅值，从而导致更高的转子损耗。然而，由于转子损耗通常低于定子损耗（在图15中，转子损耗约为定子损耗的1/3），因此本文所提策略带来的定子损耗降低完全补偿了转子损耗的增加，从而使得总焦耳损耗更低。

从图15的第三行可以看出，由于$\phi_r$值较低，所提策略显著降低了铁损$W_{Fe}$。这一结果可能对总效率产生显著影响，因为在整个运行周期中，铁损可能占主导地位。事实上，在超过额定速度值后，电机电压接近1标幺值，而定子电流远未达到额定值（图14）。电池组提供的能量$W_b$如第四行所示，计算时忽略了变换器损耗。需要注意的是，这一假设在评估所提策略的优势时是保守的。实际上，通过最小化定子电流幅值，该方法对变换器的开关损耗和导通损耗均产生了积极影响。此外，仅依赖于有功功率的电化学电池损耗也有所降低。节能效果$\Delta W_b$显示在最后一行。可以看出，所提出的该策略确保了显著的节能效果，尤其是在低速和中速运行周期部分，节能效果可超过20%。

VI. 结论

本文重点研究了作为电动汽车（EV）牵引电机的异步电机的控制。如感应电机模型所示，期望的牵引力轨迹并不能唯一确定电机的电流分量值。因此，控制策略具有一个可利用的自由度。由于汽车应用通常具有重复性转矩变化的特点，所提出的最优策略已被采用在实现最大转矩每安培（MTPA）比率时，不仅考虑稳态运行，还考虑由于转矩阶跃变化引起的瞬态运行。特别地，选择电流幅值平方的积分作为待最小化的目标函数，并将该问题视为一个变分法问题，从而得到相应的微分欧拉-拉格朗日方程。该解提供了d轴和q轴电流分量的时间轨迹的闭式解析表达式，以在转矩需求发生阶跃变化时最小化定子电流幅值。所提出的控制策略已通过数值和实验验证。

相应电气量的定性行为已被研究，并与其他方法进行了比较策略。该比较包括传统的磁场定向控制策略，其在最大磁通下运行，以牺牲效率为代价来提升动态性能，以及经过改进的磁场定向控制策略，使其在稳态下实现最大转矩每安培比（TM）。所提出的方法显著降低了定子铜损和铁损。此外，与传统最大转矩每安培（TM）相比，其表现出更优的转矩响应。在小尺寸实验室样机上进行的实验测试结果与数值研究完全一致，验证了仿真环境的有效性，该仿真环境已被用于评估全尺寸电动汽车在Worldwide harmonized轻型车辆测试程序（WLTP）。实验和数值输出均凸显了所提出方法的有效性，表明电机损耗显著降低，使得1.1千瓦实验室装置节能约50-70百分比，全尺寸车辆节能5-25百分比。