快速排序算法详解与应用-CSDN博客

本文链接：https://blog.csdn.net/catpico/article/details/123039214

基本介绍

在平均状况下，排序 n 个项目要 $O (n l o g n)$ 次比较。在最坏状况下则需要 $Ο(n^2)$ 次比较，但这种状况并不常见。事实上，快速排序通常明显比其他 Ο(nlogn) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

优势：
快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

算法步骤

从数列中挑出一个元素，称为 “基准”（pivot）;
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

对于下图：此时有1和8交换，从而让smaller的一起，larger的一起。
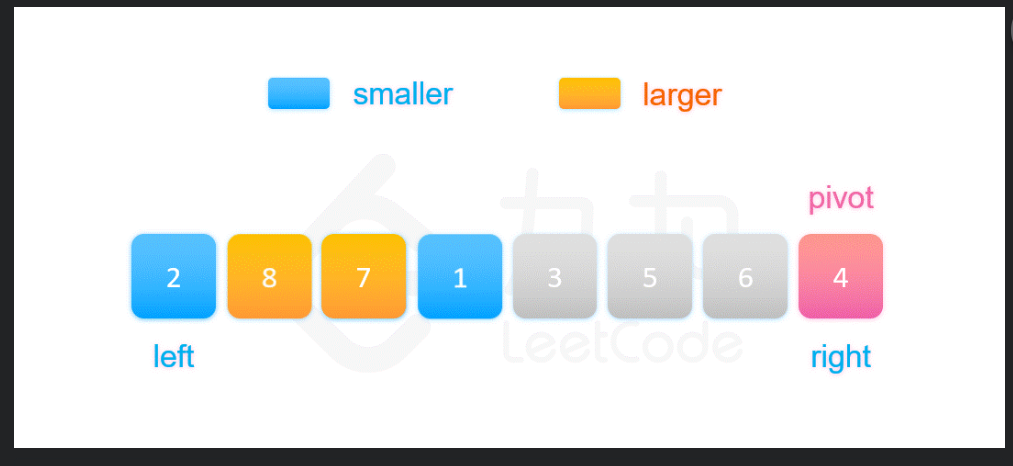
在这里插入图片描述
再让3和7交换：

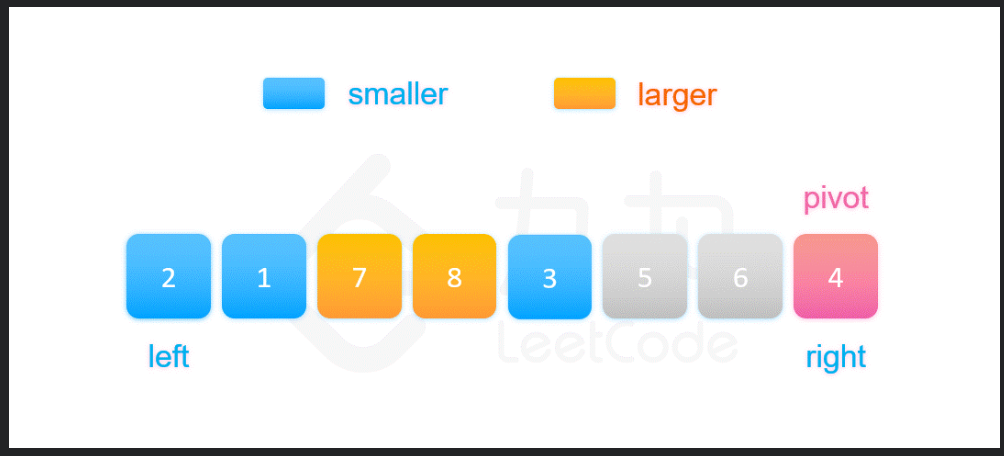
在这里插入图片描述
最后让4和8交换：

划分完之后，左子数组的所有数字小于等于基准数，右子数组的所有数字大于等于基准数

递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序

注意的几个点：

算法思想：分而治之（分治思想），与「归并排序」不同，「快速排序」在「分」这件事情上不像「归并排序」无脑地一分为二，而是采用了 partition 的方法，因此就没有「合」的过程。
实现细节（注意事项）：（针对特殊测试用例：顺序数组或者逆序数组）一定要随机化选择切分元素（pivot），否则在输入数组是有序数组或者是逆序数组的时候，快速排序会变得非常慢（等同于冒泡排序或者「选择排序」）

步骤过程可以参考这个可视化网站：
https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

编程举例

@力扣912.排序数组

class Solution {
    int partition(vector<int>& nums, int l, int r) {
        int pivot = nums[r];
        int i = l - 1;
        for (int j = l; j <= r - 1; ++j) {
            if (nums[j] <= pivot) {
                i = i + 1;
                swap(nums[i], nums[j]);
            }
        }
        swap(nums[i + 1], nums[r]);
        return i + 1;
    }
    int randomized_partition(vector<int>& nums, int l, int r) {
        int i = rand() % (r - l + 1) + l; // 随机选一个作为我们的主元
        swap(nums[r], nums[i]);
        return partition(nums, l, r);
    }
    void randomized_quicksort(vector<int>& nums, int l, int r) {
        if (l < r) {
            int pos = randomized_partition(nums, l, r);
            randomized_quicksort(nums, l, pos - 1);
            randomized_quicksort(nums, pos + 1, r);
        }
    }
public:
    vector<int> sortArray(vector<int>& nums) {
        srand((unsigned)time(NULL));
        randomized_quicksort(nums, 0, (int)nums.size() - 1);
        return nums;
    }
};

时间复杂度：基于随机选取主元的快速排序时间复杂度为期望 O(nlog⁡n)，其中 n 为数组的长度。详细证明过程可以见《算法导论》第七章。

空间复杂度：O(h)，其中 h 为快速排序递归调用的层数。我们需要额外的 O(h)的递归调用的栈空间，由于划分的结果不同导致了快速排序递归调用的层数也会不同，最坏情况下需 O(n)的空间，最优情况下每次都平衡，此时整个递归树高度为 logn，空间复杂度为O(logn)。

@力扣215.数组中的第K个最大元素

class Solution {
public:
    int quickSelect(vector<int>& a, int l, int r, int index) {
        int q = randomPartition(a, l, r);
        if (q == index) {
            return a[q];
        } else {
            return q < index ? quickSelect(a, q + 1, r, index) : quickSelect(a, l, q - 1, index);
        }
    }

    inline int randomPartition(vector<int>& a, int l, int r) {
        int i = rand() % (r - l + 1) + l;
        swap(a[i], a[r]);
        return partition(a, l, r);
    }

    inline int partition(vector<int>& a, int l, int r) {
        int x = a[r], i = l - 1;
        for (int j = l; j < r; ++j) {
            if (a[j] <= x) {
                swap(a[++i], a[j]);
            }
        }
        swap(a[i + 1], a[r]);
        return i + 1;
    }

    int findKthLargest(vector<int>& nums, int k) {
        srand(time(0));
        return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
    }
};

@力扣最小的k个数

法一：

在这里插入图片描述递归：对左子数组和右子数组递归执行哨兵划分，直至子数组长度为 1 时终止递归，即可完成对整个数组的排序。快速排序和二分法的原理类似，都是以 logn时间复杂度实现搜索区间缩小。

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        quickSort(arr, 0, arr.size() - 1);
        vector<int> res;
        res.assign(arr.begin(), arr.begin() + k);
        return res;
    }
private:
    void quickSort(vector<int>& arr, int l, int r) {
        // 子数组长度为 1 时终止递归
        if (l >= r) return;
        // 哨兵划分操作（以 arr[l] 作为基准数）
        int i = l, j = r;
        while (i < j) {
            while (i < j && arr[j] >= arr[l]) j--;
            while (i < j && arr[i] <= arr[l]) i++;
            swap(arr[i], arr[j]);
        }
        swap(arr[i], arr[l]);
        // 递归左（右）子数组执行哨兵划分
        quickSort(arr, l, i - 1);
        quickSort(arr, i + 1, r);
    }
};

时间复杂度O(Nlog⁡N)：库函数、快排等排序算法的平均时间复杂度为 O(Nlog⁡N) 。
空间复杂度 O(N)：快速排序的递归深度最好（平均）为 O(log⁡N)，最差情况（即输入数组完全倒序）为 O(N)。

法二：

方法二：基于快速排序的数组划分

题目只要求返回最小的 k 个数，对这 k 个数的顺序并没有要求。因此，只需要将数组划分为最小的 k个数和其他数字两部分即可，而快速排序的哨兵划分可完成此目标。

根据快速排序原理，如果某次哨兵划分后基准数正好是第 k+1 小的数字，那么此时基准数左边的所有数字便是题目所求的最小的 k 个数。

根据此思路，考虑在每次哨兵划分后，判断基准数在数组中的索引是否等于 kkk ，若 true 则直接返回此时数组的前 k个数字即可。

注意，此时 quick_sort() 的功能不是排序整个数组，而是搜索并返回最小的 k 个数。
在这里插入图片描述

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        if (k >= arr.size()) return arr;
        return quickSort(arr, k, 0, arr.size() - 1);
    }
private:
    vector<int> quickSort(vector<int>& arr, int k, int l, int r) {
        int i = l, j = r;
        while (i < j) {
            while (i < j && arr[j] >= arr[l]) j--;
            while (i < j && arr[i] <= arr[l]) i++;
            swap(arr[i], arr[j]);
        }
        swap(arr[i], arr[l]);
        if (i > k) return quickSort(arr, k, l, i - 1);
        if (i < k) return quickSort(arr, k, i + 1, r);
        vector<int> res;
        res.assign(arr.begin(), arr.begin() + k);
        return res;
    }
};

时间复杂度 O(N)：其中 N为数组元素数量；对于长度为 N的数组执行哨兵划分操作的时间复杂度为 O(N)；每轮哨兵划分后根据 k和 i的大小关系选择递归，由于 i 分布的随机性，则向下递归子数组的平均长度为 N/2 ；因此平均情况下，哨兵划分操作一共有 N + N/2 + N/4 +… + N/N =2N−1 （等比数列求和），即总体时间复杂度为 O(N)。
空间复杂度 O(log⁡N)：划分函数的平均递归深度为 O(log⁡N)。

@力扣最接近原点的K个点

class Solution {
private:
    mt19937 gen{random_device{}()};

public:
    void random_select(vector<vector<int>>& points, int left, int right, int k) {
        int pivot_id = uniform_int_distribution<int>{left, right}(gen);
        int pivot = points[pivot_id][0] * points[pivot_id][0] + points[pivot_id][1] * points[pivot_id][1];
        swap(points[right], points[pivot_id]);
        int i = left - 1;
        for (int j = left; j < right; ++j) {
            int dist = points[j][0] * points[j][0] + points[j][1] * points[j][1];
            if (dist <= pivot) {
                ++i;
                swap(points[i], points[j]);
            }
        }
        ++i;
        swap(points[i], points[right]);
        // [left, i-1] 都小于等于 pivot, [i+1, right] 都大于 pivot
        if (k < i - left + 1) {
            random_select(points, left, i - 1, k);
        }
        else if (k > i - left + 1) {
            random_select(points, i + 1, right, k - (i - left + 1));
        }
    }

    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        int n = points.size();
        random_select(points, 0, n - 1, k);
        return {points.begin(), points.begin() + k};
    }
};