KMP

最新推荐文章于 2021-04-24 20:16:51 发布

yi淼菌君

最新推荐文章于 2021-04-24 20:16:51 发布

阅读量513

点赞数

KMP字符串模式匹配详解

KMP 字符串模式匹配通俗点说就是一种在一个字符串中定位另一个串的高效算法。简单匹配算法的时间复杂度为 O(m*n);KMP 匹配算法。可以证明它的时间复杂度为 O(m+n). 。

一.简单匹配算法

先来看一个简单匹配算法的函数：

int Index_BF ( char S [ ], char T [ ], int pos )

{

/* 若串 S 中从第 pos(S 的下标 0 ≤ pos<StrLength(S)) 个字符

起存在和串 T 相同的子串，则称匹配成功，返回第一个

这样的子串在串 S 中的下标，否则返回 -1 */

int i = pos, j = 0;

while ( S[i+j] != '/0'&& T[j] != '/0')

if ( S[i+j] == T[j] )

j ++; // 继续比较后一字符

else

{

i ++; j = 0; // 重新开始新的一轮匹配

}

if ( T[j] == '/0')

return i; // 匹配成功返回下标

else

return -1; // 串 S 中 ( 第 pos 个字符起 ) 不存在和串 T 相同的子串

} // Index_BF
此算法的思想是直截了当的：将主串 S 中某个位置 i 起始的子串和模式串 T 相比较。即从 j=0 起比较 S[i+j] 与 T[j] ，若相等，则在主串 S 中存在以 i 为起始位置匹配成功的可能性，继续往后比较 ( j 逐步增 1 ) ，直至与 T 串中最后一个字符相等为止，否则改从 S 串的下一个字符起重新开始进行下一轮的 " 匹配 " ，即将串 T 向后滑动一位，即 i 增 1 ，而 j 退回至 0 ，重新开始新一轮的匹配。

例如：在串 S= ”abcabcabdabba” 中查找 T=” abcabd” （我们可以假设从下标 0 开始） : 先是比较 S[0] 和 T[0] 是否相等，然后比较 S[1] 和 T[1] 是否相等 … 我们发现一直比较到 S[5] 和 T[5] 才不等。如图：

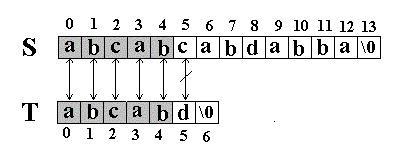
当这样一个失配发生时， T 下标必须回溯到开始， S 下标回溯的长度与 T 相同，然后 S 下标增 1, 然后再次比较。如图：

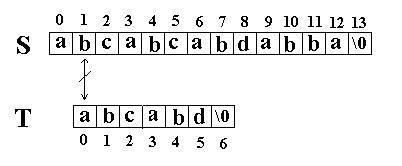
这次立刻发生了失配， T 下标又回溯到开始， S 下标增 1, 然后再次比较。如图：

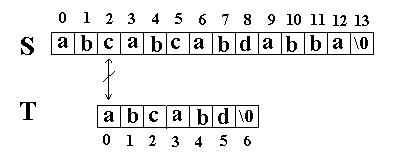
又一次发生了失配，所以 T 下标又回溯到开始， S 下标增 1, 然后再次比较。这次 T 中的所有字符都和 S 中相应的字符匹配了。函数返回 T 在 S 中的起始下标 3 。如图：

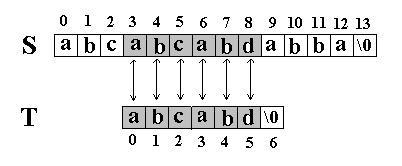
二. KMP匹配算法

还是相同的例子，在 S= ”abcabcabdabba” 中查找 T =”abcabd” ，如果使用 KMP 匹配算法，当第一次搜索到 S[5] 和 T[5] 不等后， S 下标不是回溯到 1 ， T 下标也不是回溯到开始，而是根据 T 中 T[5]==’d’ 的模式函数值（ next[5]=2 ，为什么？后面讲），直接比较 S[5] 和 T[2] 是否相等，因为相等， S 和 T 的下标同时增加 ; 因为又相等， S 和 T 的下标又同时增加。。。最终在 S 中找到了 T 。如图：

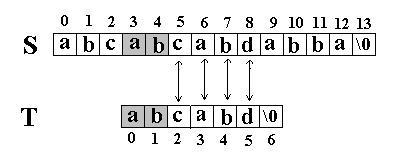
KMP 匹配算法和简单匹配算法效率比较，一个极端的例子是：

在 S= “ AAAAAA…AAB “ (100 个 A) 中查找 T=”AAAAAAAAAB”, 简单匹配算法每次都是比较到 T 的结尾，发现字符不同，然后 T 的下标回溯到开始， S 的下标也要回溯相同长度后增 1 ，继续比较。如果使用 KMP 匹配算法，就不必回溯 .

对于一般文稿中串的匹配，简单匹配算法的时间复杂度可降为 O (m+n) ，因此在多数的实际应用场合下被应用。

KMP 算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。看前面的例子。为什么 T[5]==’d’ 的模式函数值等于 2 （ next[5]=2 ），其实这个 2 表示 T[5]==’d’ 的前面有 2 个字符和开始的两个字符相同，且 T[5]==’d’ 不等于开始的两个字符之后的第三个字符（ T[2]=’c’ ） . 如图：

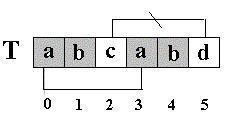
也就是说，如果开始的两个字符之后的第三个字符也为 ’d’, 那么，尽管 T[5]==’d’ 的前面有 2 个字符和开始的两个字符相同， T[5]==’d’ 的模式函数值也不为 2 ，而是为 0 。

前面我说：在 S= ”abcabcabdabba” 中查找 T =”abcabd” ，如果使用 KMP 匹配算法，当第一次搜索到 S[5] 和 T[5] 不等后， S 下标不是回溯到 1 ， T 下标也不是回溯到开始，而是根据 T 中 T[5]==’d’ 的模式函数值，直接比较 S[5] 和 T[2] 是否相等。。。为什么可以这样？

刚才我又说：“（ next[5]=2 ），其实这个 2 表示 T[5]==’d’ 的前面有 2 个字符和开始的两个字符相同”。请看图：因为， S[4] ==T[4] ， S[3] ==T[3] ，根据 next[5]=2 ，有 T[3]==T[0] ， T[4] ==T[1] ，所以 S[3]==T[0] ， S[4] ==T[1] （两对相当于间接比较过了），因此，接下来比较 S[5] 和 T[2] 是否相等。。。

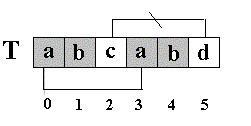
有人可能会问： S[3] 和 T[0] ， S[4] 和 T[1] 是根据 next[5]=2 间接比较相等，那 S[1] 和 T[0] ， S[2] 和 T[0] 之间又是怎么跳过，可以不比较呢？因为 S[0]=T[0] ， S[1]=T[1] ， S[2]=T[2] ，而 T[0] != T[1], T[1] != T[2],==> S[0] != S[1],S[1] != S[2], 所以 S[1] != T[0],S[2] != T[0]. 还是从理论上间接比较了。

有人疑问又来了，你分析的是不是特殊轻况啊。

假设 S 不变，在 S 中搜索 T= “ abaabd ”呢？答：这种情况，当比较到 S[2] 和 T[2] 时，发现不等，就去看 next[2] 的值， next[2]=-1 ，意思是 S[2] 已经和 T[0] 间接比较过了，不相等，接下来去比较 S[3] 和 T[0] 吧。

假设 S 不变，在 S 中搜索 T= “ abbabd ”呢？答：这种情况当比较到 S[2] 和 T[2] 时，发现不等，就去看 next[2] 的值， next[2]=0 ，意思是 S[2] 已经和 T[2] 比较过了，不相等，接下来去比较 S[2] 和 T[0] 吧。

假设 S=” abaabcabdabba ” 在 S 中搜索 T= “ abaabd ”呢？答：这种情况当比较到 S[5] 和 T[5] 时，发现不等，就去看 next[5] 的值， next[5]=2 ，意思是前面的比较过了，其中， S[5] 的前面有两个字符和 T 的开始两个相等，接下来去比较 S[5] 和 T[2] 吧。

总之，有了串的 next 值，一切搞定。那么，怎么求串的模式函数值 next[n] 呢？（本文中 next 值、模式函数值、模式值是一个意思。）

三. 怎么求串的模式值next[n]

定义：

（ 1 ） next[0]= -1 意义：任何串的第一个字符的模式值规定为 -1 。

（ 2 ） next[j]= -1 意义：模式串 T 中下标为 j 的字符，如果与首字符

相同，且 j 的前面的 1—k 个字符与开头的 1—k

个字符不等（或者相等但 T[k]==T[j] ）（ 1 ≤ k<j ）。

如： T=”abCabCad” 则 next[6]=-1 ，因 T[3]=T[6]

（ 3 ） next[j]=k 意义：模式串 T 中下标为 j 的字符，如果 j 的前面 k 个

字符与开头的 k 个字符相等，且 T[j] != T[k] （ 1 ≤ k<j ）。

即 T[0]T[1]T[2] 。。。 T[k-1]==

T[j-k]T[j-k+1]T[j-k+2]…T[j-1]

且 T[j] != T[k]. （ 1 ≤ k<j ） ;

(4) next[j]=0 意义：除（ 1 ）（ 2 ）（ 3 ）的其他情况。

举例：

01 ）求 T= “ abcac ”的模式函数的值。

next[0]= -1 根据（ 1 ）

next[1]=0 根据 (4) 因（ 3 ）有 1<=k<j; 不能说， j=1,T[j-1]==T[0]

next[2]=0 根据 (4) 因（ 3 ）有 1<=k<j; （ T[0]=a ） != （ T[1]=b ）

next[3]= -1 根据 (2)

next[4]=1 根据 (3) T[0]=T[3] 且 T[1]=T[4]

即

下标	0	1	2	3	4
T	a	b	c	a	c
next	-1	0	0	-1	1

若 T= “ abcab ”将是这样：

下标	0	1	2	3	4
T	a	b	c	a	b
next	-1	0	0	-1	0

为什么 T[0]==T[3], 还会有 next[4]=0 呢 , 因为 T[1]==T[4], 根据 (3)” 且 T[j] != T[k]” 被划入（ 4 ）。

02 ）来个复杂点的，求 T=”ababcaabc” 的模式函数的值。

next[0]= -1 根据（ 1 ）

next[1]=0 根据 (4)

next[2]=-1 根据 (2)

next[3]=0 根据 (3) 虽 T[0]=T[2] 但 T[1]=T[3] 被划入（ 4 ）

next[4]=2 根据 (3) T[0]T[1]=T[2]T[3] 且 T[2] !=T[4]

next[5]=-1 根据 (2)

next[6]=1 根据 (3) T[0]=T[5] 且 T[1]!=T[6]

next[7]=0 根据 (3) 虽 T[0]=T[6] 但 T[1]=T[7] 被划入（ 4 ）

next[8]=2 根据 (3) T[0]T[1]=T[6]T[7] 且 T[2] !=T[8]

即

下标	0	1	2	3	4	5	6	7	8
T	a	b	a	b	c	a	a	b	c
next	-1	0	-1	0	2	-1	1	0	2

只要理解了 next[3]=0 ，而不是 =1 ， next[6]=1 ，而不是 = -1 ， next[8]=2 ，而不是 = 0 ，其他的好象都容易理解。

03) 来个特殊的，求 T=”abCabCad” 的模式函数的值。

下标	0	1	2	3	4	5	6	7
T	a	b	C	a	b	C	a	d
next	-1	0	0	-1	0	0	-1	4

next[5]= 0 根据 (3) 虽 T[0]T[1]=T[3]T[4], 但 T[2]==T[5]

next[6]= -1 根据 (2) 虽前面有 abC=abC, 但 T[3]==T[6]

next[7]=4 根据 (3) 前面有 abCa=abCa, 且 T[4]!=T[7]

若 T[4]==T[7] ，即 T=” adCadCad”, 那么将是这样： next[7]=0, 而不是 = 4, 因为 T[4]==T[7].

下标	0	1	2	3	4	5	6	7
T	a	d	C	a	d	C	a	d
next	-1	0	0	-1	0	0	-1	0

如果你觉得有点懂了，那么

练习：求 T=”AAAAAAAAAAB” 的模式函数值，并用后面的求模式函数值函数验证。

意义：

next 函数值究竟是什么含义，前面说过一些，这里总结。

设在字符串 S 中查找模式串 T ，若 S[m]!=T[n], 那么，取 T[n] 的模式函数值 next[n],

1. next[n]= -1 表示 S[m] 和 T[0] 间接比较过了，不相等，下一次比较 S[m+1] 和 T[0]

2. next[n]=0 表示比较过程中产生了不相等，下一次比较 S[m] 和 T[0] 。

3. next[n]= k >0 但 k<n, 表示 ,S[m] 的前 k 个字符与 T 中的开始 k 个字符已经间接比较相等了，下一次比较 S[m] 和 T[k] 相等吗？

4. 其他值，不可能。

四. 求串T的模式值next[n]的函数

说了这么多，是不是觉得求串 T 的模式值 next[n] 很复杂呢？要叫我写个函数出来，目前来说，我宁愿去登天。好在有现成的函数，当初发明 KMP 算法，写出这个函数的先辈，令我佩服得六体投地。我等后生小子，理解起来，都要反复琢磨。下面是这个函数 :

void get_nextval(const char *T, int next[])

{

// 求模式串 T 的 next 函数值并存入数组 next 。

int j = 0, k = -1;

next[0] = -1;

while ( T[j/*+1*/] != '/0' )

{

if (k == -1 || T[j] == T[k])

{

++j; ++k;

if (T[j]!=T[k])

next[j] = k;

else

next[j] = next[k];

}// if

else

k = next[k];

} // while

这里是我加的显示部分

// for(int i=0;i<j;i++)

//{

// cout<<next[i];

//}

//cout<<endl;

} // get_nextval 　

另一种写法，也差不多。

void getNext(const char* pattern,int next[])

{

next[0]= -1;

int k=-1,j=0;

while(pattern[j] != '/0')

{

if(k!= -1 && pattern[k]!= pattern[j] )

k=next[k];

++j;++k;

if(pattern[k]== pattern[j])

next[j]=next[k];

else

next[j]=k;

}

这里是我加的显示部分

// for(int i=0;i<j;i++)

//{

// cout<<next[i];

//}

//cout<<endl;

}

下面是 KMP 模式匹配程序，各位可以用他验证。记得加入上面的函数

#include <iostream.h>

#include <string.h>

int KMP(const char *Text,const char* Pattern) //const 表示函数内部不会改变这个参数的值。

{

if( !Text||!Pattern|| Pattern[0]=='/0' || Text[0]=='/0' )//

return -1;// 空指针或空串，返回 -1 。

int len=0;

const char * c=Pattern;

while(*c++!='/0')// 移动指针比移动下标快。

{

++len;// 字符串长度。

}

int *next=new int[len+1];

get_nextval(Pattern,next);// 求 Pattern 的 next 函数值

int index=0,i=0,j=0;

while(Text[i]!='/0' && Pattern[j]!='/0' )

{

if(Text[i]== Pattern[j])

{

++i;// 继续比较后继字符

++j;

}

else

{

index += j-next[j];

if(next[j]!=-1)

j=next[j];// 模式串向右移动

else

{

j=0;

++i;

}

}//while

delete []next;

if(Pattern[j]=='/0')

return index;// 匹配成功

else

return -1;

}

int main()//abCabCad

{

char* text="bababCabCadcaabcaababcbaaaabaaacababcaabc";

char*pattern="adCadCad";

//getNext(pattern,n);

//get_nextval(pattern,n);

cout<<KMP(text,pattern)<<endl;

return 0;

}

五．其他表示模式值的方法

上面那种串的模式值表示方法是最优秀的表示方法，从串的模式值我们可以得到很多信息，以下称为第一种表示方法。第二种表示方法，虽然也定义 next[0]= -1, 但后面绝不会出现 -1 ，除了 next[0] ，其他模式值 next[j]=k(0 ≤ k<j) 的意义可以简单看成是：下标为 j 的字符的前面最多 k 个字符与开始的 k 个字符相同，这里并不要求 T[j] != T[k] 。其实 next[0] 也可以定义为 0 （后面给出的求串的模式值的函数和串的模式匹配的函数，是 next[0]=0 的），这样， next[j]=k(0 ≤ k<j) 的意义都可以简单看成是：下标为 j 的字符的前面最多 k 个字符与开始的 k 个字符相同。第三种表示方法是第一种表示方法的变形，即按第一种方法得到的模式值，每个值分别加 1 ，就得到第三种表示方法。第三种表示方法，我是从论坛上看到的，没看到详细解释，我估计是为那些这样的编程语言准备的：数组的下标从 1 开始而不是 0 。

下面给出几种方法的例子：

表一。

下标	0	1	2	3	4	5	6	7	8
T	a	b	a	b	c	a	a	b	c
(1) next	-1	0	-1	0	2	-1	1	0	2
(2) next	-1	0	0	1	2	0	1	1	2
(3) next	0	1	0	1	3	0	2	1	3

第三种表示方法 , 在我看来，意义不是那么明了，不再讨论。

表二。

下标	0	1	2	3	4
T	a	b	c	A	c
(1)next	-1	0	0	-1	1
(2)next	-1	0	0	0	1

表三。

下标	0	1	2	3	4	5	6	7
T	a	d	C	a	d	C	a	d
(1)next	-1	0	0	-1	0	0	-1	0
(2)next	-1	0	0	0	1	2	3	4

对比串的模式值第一种表示方法和第二种表示方法，看表一：

第一种表示方法 next[2]= -1, 表示 T[2]=T[0] ，且 T[2-1] !=T[0]

第二种表示方法 next[2]= 0, 表示 T[2-1] !=T[0], 但并不管 T[0] 和 T[2] 相不相等。

第一种表示方法 next[3]= 0, 表示虽然 T[2]=T[0] ，但 T[1] ==T[3]

第二种表示方法 next[3]= 1, 表示 T[2] =T[0], 他并不管 T[1] 和 T[3] 相不相等。

第一种表示方法 next[5]= -1, 表示 T[5]=T[0] ，且 T[4] !=T[0] ， T[3]T[4] !=T[0]T[1] ， T[2]T[3]T[4] !=T[0]T[1]T[2]

第二种表示方法 next[5]= 0, 表示 T[4] !=T[0] ， T[3]T[4] !=T[0]T[1] ， T[2]T[3]T[4] !=T[0]T[1]T[2] ，但并不管 T[0] 和 T[5] 相不相等。换句话说：就算 T[5]==’x’, 或 T[5]==’y’,T[5]==’9’, 也有 next[5]= 0 。

从这里我们可以看到：串的模式值第一种表示方法能表示更多的信息，第二种表示方法更单纯，不容易搞错。当然，用第一种表示方法写出的模式匹配函数效率更高。比如说，在串 S= “ adCadCBdadCadCad 9876543 ”中匹配串 T= “ adCadCad ” , 用第一种表示方法写出的模式匹配函数 , 当比较到 S[6] != T[6] 时，取 next[6]= -1 （表三） , 它可以表示这样许多信息： S[3]S[4]S[5]==T[3]T[4]T[5]==T[0]T[1]T[2] ，而 S[6] != T[6] ， T[6]==T[3]==T[0] ，所以 S[6] != T[0], 接下来比较 S[7] 和 T[0] 吧。如果用第二种表示方法写出的模式匹配函数 , 当比较到 S[6] != T[6] 时，取 next[6]= 3 （表三） , 它只能表示： S[3]S[4]S[5]== T[3]T[4]T[5]==T[0]T[1]T[2] ，但不能确定 T[6] 与 T[3] 相不相等，所以，接下来比较 S[6] 和 T[3]; 又不相等，取 next[3]= 0 ，它表示 S[3]S[4]S[5]== T[0]T[1]T[2] ，但不会确定 T[3] 与 T[0] 相不相等，即 S[6] 和 T[0] 相不相等，所以接下来比较 S[6] 和 T[0] ，确定它们不相等，然后才会比较 S[7] 和 T[0] 。是不是比用第一种表示方法写出的模式匹配函数多绕了几个弯。

为什么，在讲明第一种表示方法后，还要讲没有第一种表示方法好的第二种表示方法？原因是：最开始，我看严蔚敏的一个讲座，她给出的模式值表示方法是我这里的第二种表示方法，如图：

她说：“ next 函数值的含义是：当出现 S[i] !=T[j] 时，下一次的比较应该在 S[i] 和 T[next[j]] 之间进行。”虽简洁，但不明了，反复几遍也没明白为什么。而她给出的算法求出的模式值是我这里说的第一种表示方法 next 值，就是前面的 get_nextval() 函数。匹配算法也是有瑕疵的。于是我在这里发帖说她错了：

http://community.csdn.net/Expert/topic/4413/4413398.xml?temp=.2027246

现在看来，她没有错，不过有张冠李戴之嫌。我不知道，是否有人第一次学到这里，不参考其他资料和明白人讲解的情况下，就能搞懂这个算法（我的意思是不仅是算法的大致思想，而是为什么定义和例子中 next[j]=k(0 ≤ k<j) ，而算法中 next[j]=k(-1 ≤ k<j) ）。凭良心说：光看这个讲座，我就对这个教受十分敬佩，不仅讲课讲得好，声音悦耳，而且这门课讲得层次分明，恰到好处。在KMP这个问题上出了点小差错，可能是编书的时候，在这本书上抄下了例子，在那本书上抄下了算法，结果不怎么对得上号。因为我没找到原书，而据有的网友说，书上已不是这样，也许吧。说起来，教授们研究的问题比这个高深不知多少倍，哪有时间推演这个小算法呢。总之，瑕不掩玉。

书归正传，下面给出我写的求第二种表示方法表示的模式值的函数 , 为了从 S 的任何位置开始匹配 T ，“当出现 S[i] !=T[j] 时，下一次的比较应该在 S[i] 和 T[next[j]] 之间进行。” 定义 next[0]=0 。

v oid myget_nextval(const char *T, int next[])

{

// 求模式串 T 的 next 函数值（第二种表示方法）并存入数组 next 。

int j = 1, k = 0;

next[0] = 0;

while ( T[j] != '/0' )

{

if(T[j] == T[k])

{

next[j] = k;

++j; ++k;

}

else if(T[j] != T[0])

{

next[j] = k;

++j;

k=0;

}

else

{

next[j] = k;

++j;

k=1;

}

}//while

for(int i=0;i<j;i++)

{

cout<<next[i];

}

cout<<endl;

}// myget_nextval

下面是模式值使用第二种表示方法的匹配函数（ next[0]=0 ）

int my_KMP(char *S, char *T, int pos)

{

int i = pos, j = 0;//pos(S 的下标 0 ≤ pos<StrLength(S))

while ( S[i] != '/0' && T[j] != '/0' )

{

if (S[i] == T[j] )

{

++i;

++j; // 继续比较后继字符

}

else // a b a b c a a b c

// 0 0 0 1 2 0 1 1 2

{ //-1 0 -1 0 2 -1 1 0 2

i++;

j = next[j]; /* 当出现 S[i] !=T[j] 时，

下一次的比较应该在 S[i] 和 T[next[j]] 之间进行。要求 next[0]=0 。

在这两个简单示范函数间使用全局数组 next[] 传值。 */

}

}//while

if ( T[j] == '/0' )

return (i-j); // 匹配成功

else

return -1;

} // my_KMP

六．后话--KMP的历史

[ 这段话是抄的 ]

Cook 于 1970 年证明的一个理论得到，任何一个可以使用被称为下推自动机的计算机抽象模型来解决的问题，也可以使用一个实际的计算机（更精确的说，使用一个随机存取机）在与问题规模对应的时间内解决。特别地，这个理论暗示存在着一个算法可以在大约 m+n 的时间内解决模式匹配问题，这里 m 和 n 分别是存储文本和模式串数组的最大索引。 Knuth 和 Pratt 努力地重建了 Cook 的证明，由此创建了这个模式匹配算法。大概是同一时间， Morris 在考虑设计一个文本编辑器的实际问题的过程中创建了差不多是同样的算法。这里可以看到并不是所有的算法都是“灵光一现”中被发现的，而理论化的计算机科学确实在一些时候会应用到实际的应用中。