动态规划——吹气球

问题描述

有n个气球，编号为0到n-1，每个气球都有一个分数，存在nums数组中。每次吹气球i可以得到的分数为 nums[left] * nums[i] * nums[right]，left和right分别表示i气球相邻的两个气球。当i气球被吹爆后，其左右两气球即为相邻。要求吹爆所有气球，得到最多的分数。

样例

给出 [4, 1, 5, 10]
返回 270

nums = [4, 1, 5, 10] burst 1, 得分 4 * 1 * 5 = 20
nums = [4, 5, 10]    burst 5, 得分 4 * 5 * 10 = 200 
nums = [4, 10]       burst 4, 得分 1 * 4 * 10 = 40
nums = [10]          burst 10, 得分 1 * 10 * 1 = 10

总共的分数为 20 + 200 + 40 + 10 = 270

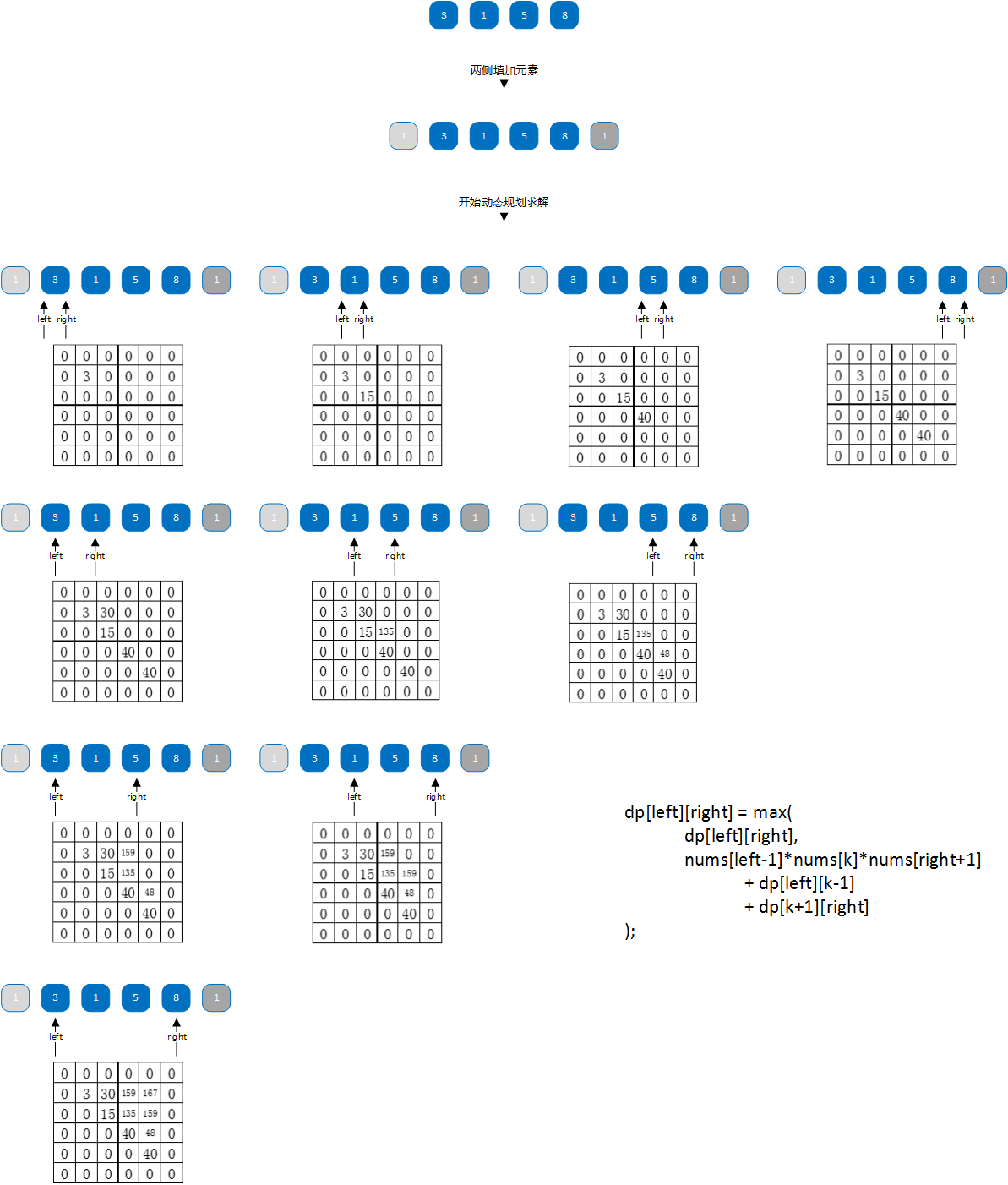
分析

代码

class Solution {
public:
    /**
     * @param nums a list of integer
     * @return an integer, maximum coins
     */  
    int maxCoins(vector<int>& nums) {
        // Write your code here
        nums.insert(nums.begin(), 1);
        nums.push_back(1);
        vector<vector<int>> dp(nums.size(), vector<int>(nums.size()));
        
        int len = nums.size() - 2;
        
        for(int i=1; i<=len; i++){
            for (int left = 1; left <= len - i + 1; left++) {
                int right = left + i - 1;
                for (int k = left; k <= left + i - 1; k++ ){
                    dp[left][right] = max(dp[left][right],
                        dp[left][k-1]+dp[k+1][right]+nums[left-1]*nums[k]*nums[right+1]);
                }
            }
        }
        
        return dp[1][len];
    }
};