内接多边形的极限是圆吗

马同学图解数学

于 2022-05-19 12:50:17 发布

阅读量530

点赞数

分类专栏：高等数学文章标签：高等数学微积分几何学

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/ccnt_2012/article/details/124860866

版权

内接正多边形无穷边圆的定义极限面积欧几里得几何

关键词由CSDN通过智能技术生成

高等数学专栏收录该内容

44 篇文章

订阅专栏

圆的面积(下)--内接正多边形的极限是圆吗

1 问题

在上一个视频中，我们根据内接多边形不断靠近圆的思想，推出了无穷边形的面积为 $\pi r^2$ ，继而得到了圆的面积为 $\pi r^2$

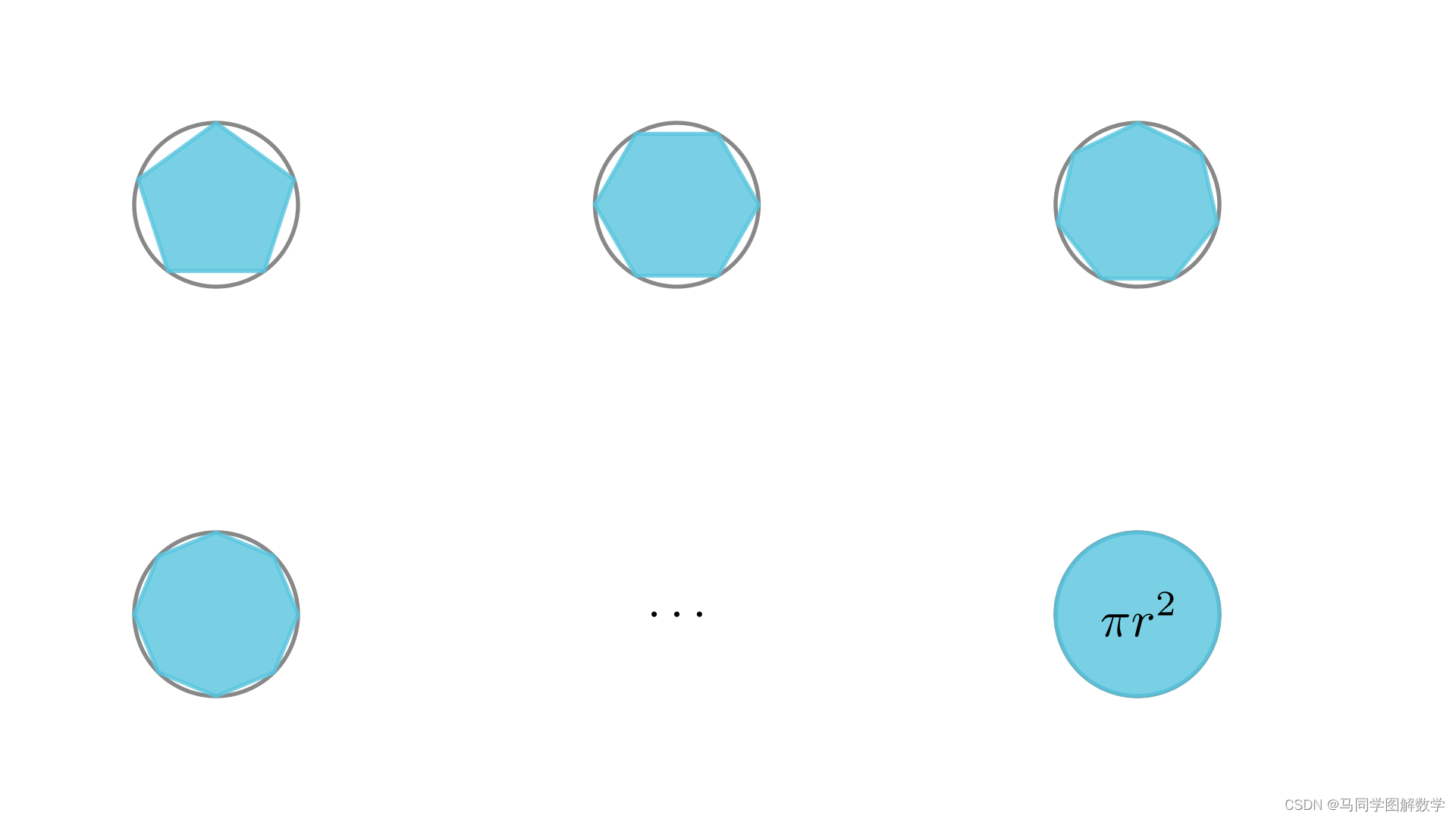
但是，这里存在一个逻辑漏洞,内接正五边形不是圆、内接正六边形不是圆,内接正七、正八边形都不是圆。既然之前的多边形都不是圆，那么最终得到的无穷多边形的面积真的是圆的面积吗？本视频就来回答这个问题

2 思路

先说思路，首先回忆一下圆的定义。根据欧几里得的《几何原本》定义，圆是到定点的距离等于定长的点的集合

如果，内接多边形增加到无穷多边时,多边形上的每个点到圆心的距离都相等,那么就能说明该无穷多边形就是圆。

那无穷多边形是这样的吗？

3 直观

无穷多边形咱不太清楚，但是对于五边形而言，边上的点到圆心的距离并不相等。其中，距离圆心最远的点，是顶点。距离最近的点是，过原点向底边所做垂线得到的垂足。

如果最长距离与最短距离相等，那么多边形上每个点到圆心的距离就都相等了。而随着边数的增加，我们可以看到，这两者的距离确实是在靠近

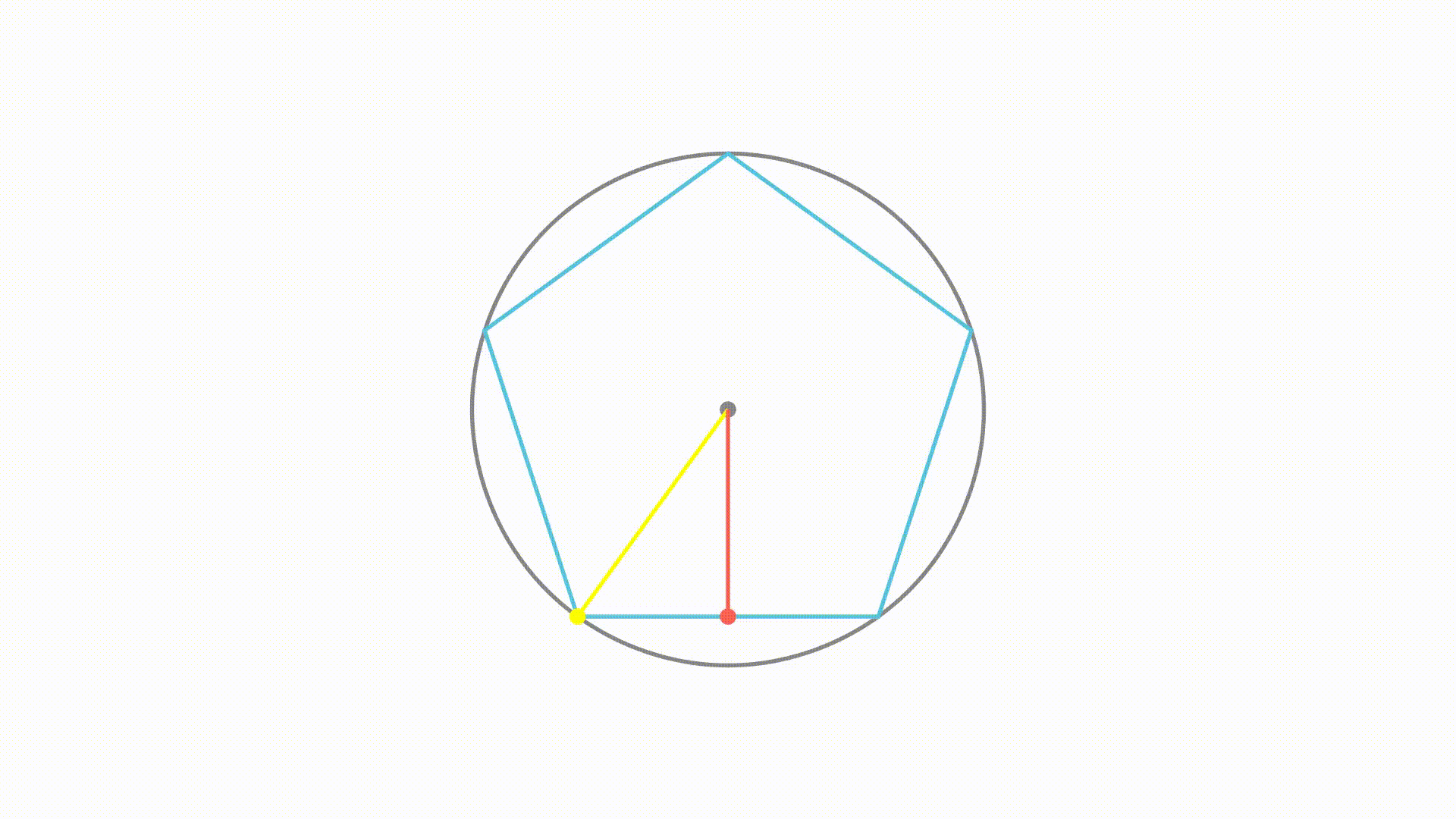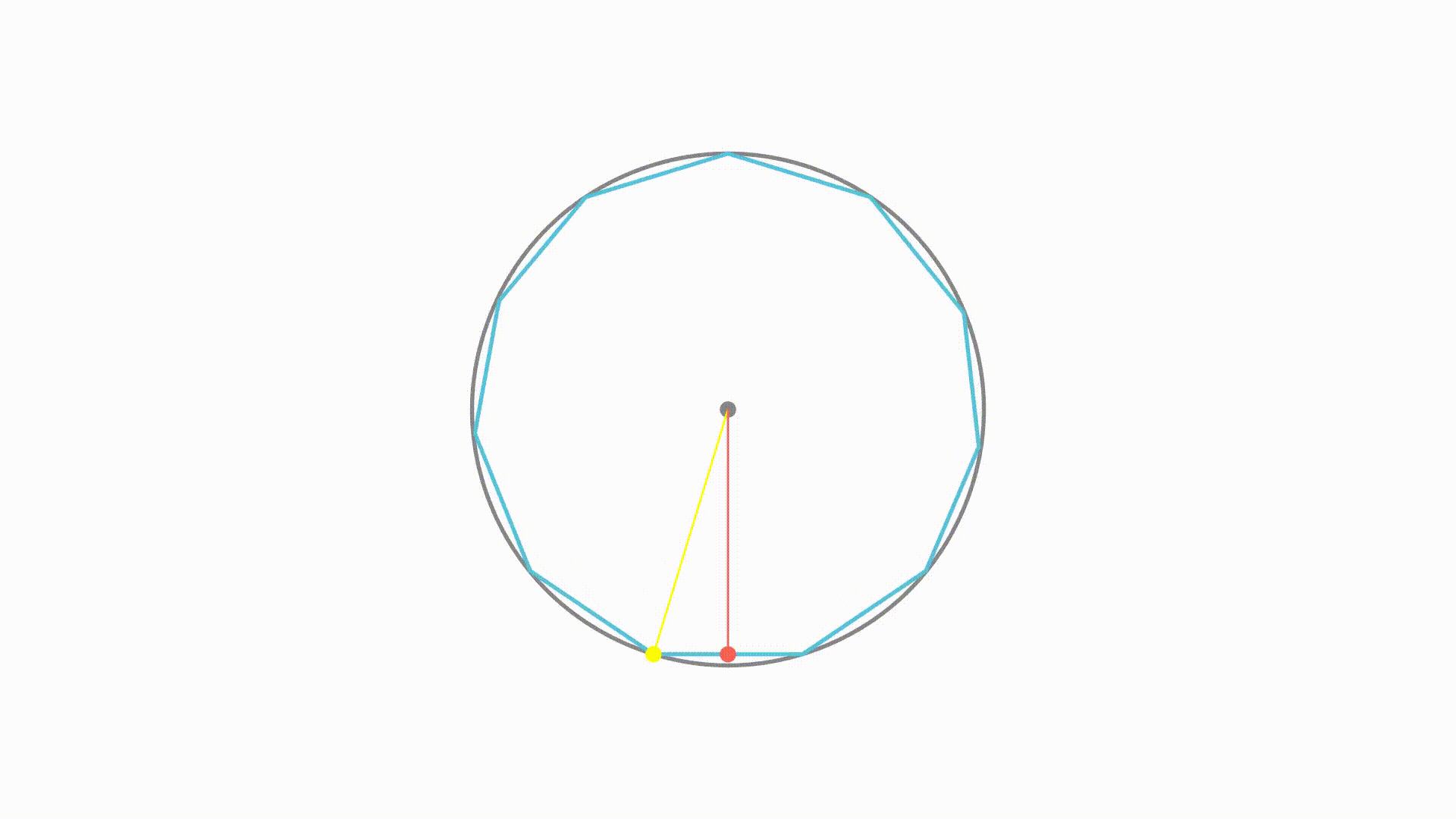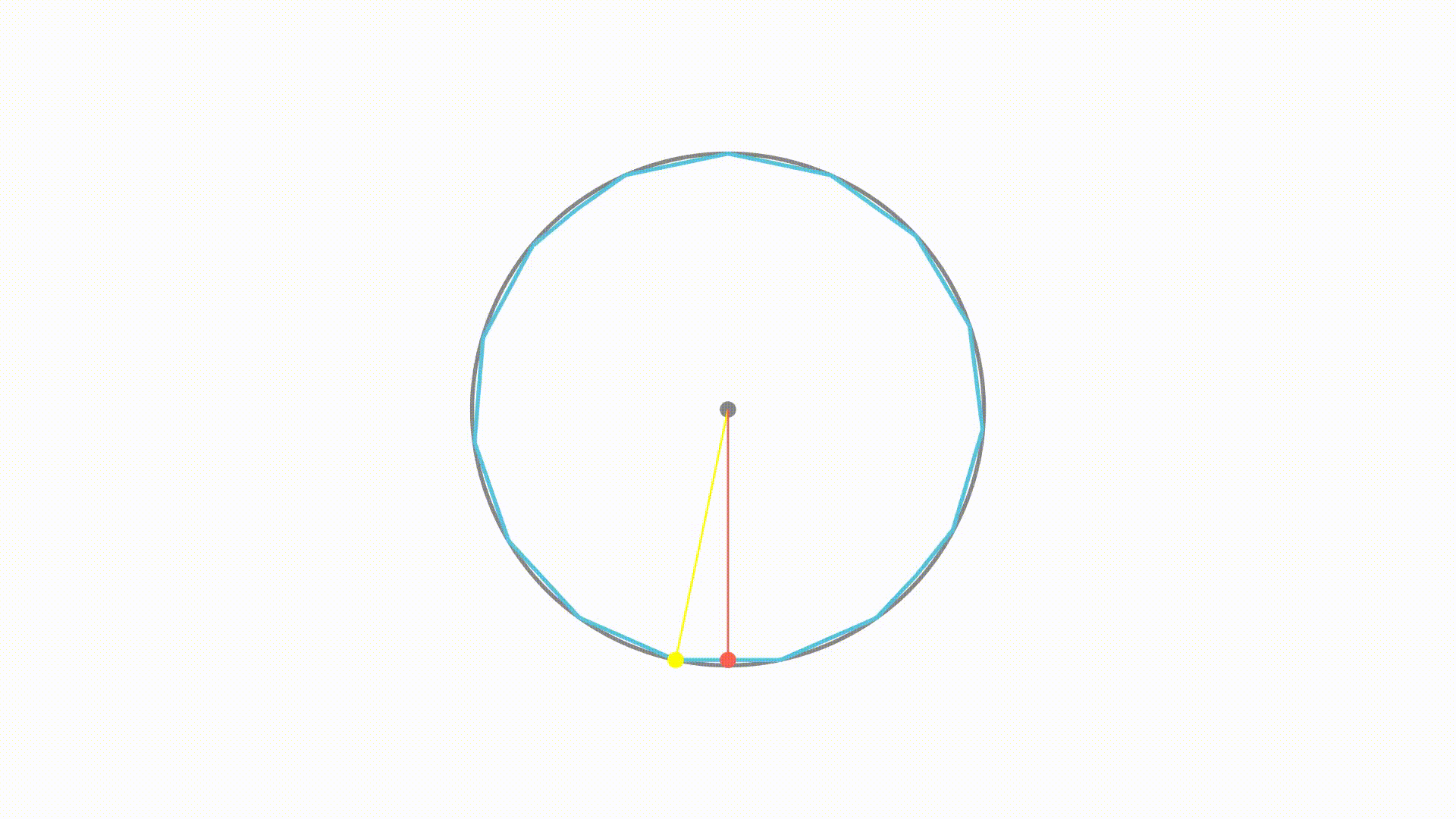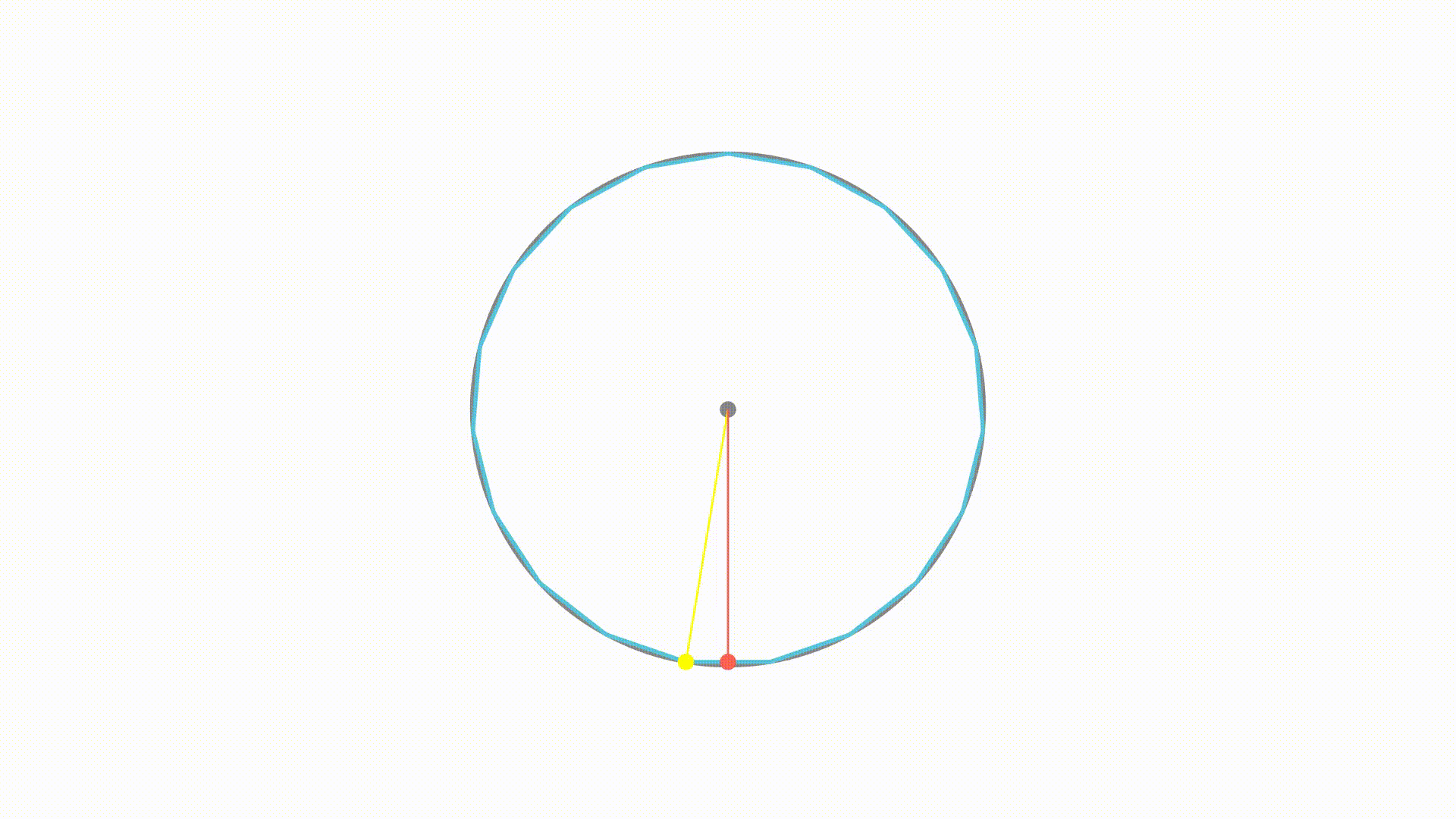
最终会不会相等呢？下面我们来证明一下

4 验证

还是画出内接正五边形，连接圆心和顶点得到最长的距离，假设其长度为 $r$ ,过圆心向其中一条边作垂线得到最短的距离。容易知道由二者产生的夹角为 $\frac{\pi}{n}$ (这里为五边形， $n$ 就等于5)。根据三角函数的知识，很容易得到最短的距离 $r\cos(\pi/n)$

因为当 $n$ 趋于无穷时， $\cos(\pi/n)$ 的极限为1,所以最短距离的极限就为 $r$ 。

$\lim_{n\to\infty}r\cos(\pi/n)=r$

这就意味着最长的距离、最短的距离在边数为无穷时会相等。所以内接无穷边多边形就是圆。那么根据内接无穷边多边形的面积为 $\pi r^2$ ,就可以推出圆的面积为 $\pi r^2$

马同学马同学提供线性代数,微积分,概率论与数理统计,机器学习等知识讲解https://www.matongxue.com/madocs/2153/

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

打赏作者

马同学图解数学 你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20

扫码支付：¥1

获取中

扫码支付

您的余额不足，请更换扫码支付或充值

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。