博客探讨了卡塔兰数的定义，即从(0,0)到(n,n)的路径计数问题，不越过直线y=x。通过数学分析，证明了C(2n,n)/(n+1)为正确答案，并提出了一种不常见但巧妙的证明方法，通过路径的转化来展示f(0)=f(2)=...=f(2n)。此外，还讨论了当路径与y=x斜率相等时的情况，并给出了相关的高精度计算问题HDU1023。"
121567537,11062165,STM32f103 OLED滚屏显示长字符实现,"['嵌入式开发', 'STM32', 'OLED显示屏', '驱动编程', '嵌入式硬件']
定义:从(0,0)到(n,n),不越过(可以接触)直线y=x(即每一步的落脚点都满足y>=x)，且每次只能往上或往右走。求方案数。
结果:C(2n,n)-C(2n,n-1) (编程是可以实现小数据的)
n比较小时可以枚举，不过n可能会很大
证明方法:有很多种，自己上维基百科就能搜到(https://en.wikipedia.org/wiki/Catalan_number)，这里给大家介绍一种不太常见的方法。
注意到答案为C(2n,n)/(n+1)
若不要求不越过y=x，答案为C(2n,n) (求法应该知道吧)
所以我们想到：定义p(l)为任意一条路径l在y=x下方所行走的路径的长度和。显然2|p(l)
图中p为4，(图直接从维基百科上复制的)
设满足p(l)=k的路径条数为f(k)，则f(0)即为所求
我们证明：f(0)=f(2)=...=f(2n)
首先想到直接证。不过如果可以就求完了。
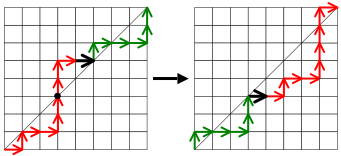
其次想到化归。我们证明任意一条满足p(l)=2k的路径l都可以化归为满足p(l')=2k+2的l'(2k-2同理)
如图，黑色箭头为调整箭头(将l划分为若干个箭头，第一个向右且恰好碰到y=x的箭头)，记为B
剩下的部分，B前面的所有箭头记为A(红色部分)，后面的记为C(绿色部分)
则路径l可记为A-
最低0.47元/天 解锁文章
扫一扫
6381
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
