谷歌提出超越Transformer的新架构Titans技术报告

-Titans: Learning to Memorize at Test Time

Ali Behrouz† , Peilin Zhong† , and Vahab Mirrokni†

Google Research

摘要 

超过十年来，人们已经进行了大量关于如何有效利用循环模型和注意力的研究。虽然循环模型旨在将数据压缩成固定大小的记忆（称为隐藏状态），但注意力允许关注整个上下文窗口，捕捉所有标记的直接依赖关系。然而，这种更准确的依赖建模会带来二次成本，限制模型只能处理固定长度的上下文。我们提出了一个新的神经长期记忆模块，该模块学会记忆历史上下文，并帮助注意力把焦点放在当前上下文，同时利用长记忆的信息。我们展示了这种神经记忆在训练时具有快速可并行化的优势，同时保持了快速的推理速度。从记忆的角度看，我们认为注意力由于其有限的上下文但准确的依赖建模，类似于短期记忆，而神经记忆由于其能够记忆数据，更像是长期、更持久的记忆。基于这两个模块，我们引入了一种新的架构系列，称为Titans，并提出了三种变体来解决如何有效地将记忆结合到这种架构中。我们在语言建模、常识推理、基因组学和时间序列任务的实验结果表明，Titans比Transformers和最近的现代线性循环模型更有效。相比基线，它们在大海捞针任务中可以有效地扩展到超过2M的上下文窗口大小，并具有更高的准确性。

“记忆的真正艺术是注意力的艺术！”—萨缪尔·约翰逊 ，1787

目录

1介绍

1.1记忆视角

1.2贡献和路线图

22.初步工作

2.1背景

3学习如何在测试时记忆

3.1长期记忆

3.2如何并行化长期记忆训练

3.3持久性内存

4如何融入记忆？

4.1记忆作为背景

4.2门控记忆

4.3内存作为一层

4.4架构细节

5实验

5.1实验设置

5.2语言建模

5.3大海捞针

5.4BABILong基准测试

5.5深度记忆的效应

5.6时间序列预测训练吞吐量

5.7DNA建模

5.8效率

5.9消融研究

6结论

参考文献

A相关工作

A.1线性递归模型

A.2基于Transformer的架构

A.3测试时间训练和快速权重程序

B语言模型和常识推理数据集

C长期记忆模块（LMM）作为序列模型

1介绍

Transformer，纯基于注意力的架构（Vaswani等，2017年），已经被确定为序列建模中的最先进模型，主要是由于它们具有上下文学习的能力和在规模上的学习能力（Kaplan等，2020年）。Transformers的主要构建模块——注意力模块——作为关联性记忆块（Bietti等，2024年）发挥作用，它们学习存储键值关联并通过计算查询Q（即搜索信号）和键K（即上下文）之间的成对相似度来检索它们。因此，根据设计，Transformer的输出仅在当前上下文窗口中的Token的直接依赖条件下。然而，这种对依赖关系的准确建模会带来关于上下文长度的二次时间和内存复杂度。在复杂的现实世界任务中（例如，语言建模（N.F.Liu等，2024年），视频理解（C.-Y.Wu等，2019年），长期时间序列预测（H.Zhou等，2021年）），上下文窗口可能变得非常大，使得Transformers在这些下游任务中的适用性有挑战性。

为了解决Transformer的可伸缩性问题，最近的研究旨在设计不同变体的线性Transformer（Kacham, Mirrokni和P. Zhong 2024; Katharopoulos等，2020年; S. Yang，B. Wang，Shen等，2024年），其中在注意力机制中用核函数替代了softmax（详见§2.1），导致内存消耗显著减少。尽管线性Transformer具有高效性和能够扩展到更长的上下文，但与Transformer相比，线性Transformer在性能上并不具备竞争力，因为核技巧使模型成为了线性递归网络，在其中数据被压缩为矩阵值状态（Katharopoulos等，2020年）。然而，线性递归（或线性Transformer）模型带来了一个矛盾的事实：一方面，我们使用这些线性模型来提升可伸缩性和效率（线性vs.二次复杂性），这些优势在非常长的上下文中表现出来;另一方面，一个非常长的上下文无法被适当地压缩为小的矢量值或矩阵值状态（S. Wang 2024）。

此外，除了效率之外，大多数现有的架构，从Hopfield网络（Hopfield 1982）到LSTMs（Jürgen Schmidhuber和Hochreiter 1997）和Transformers（Vaswani等，2017年），在处理泛化、长度外推和/或推理（Anil等，2022年；Qin，Y. Zhong和Deng 2024年）时面临挑战，所有这些都是许多复杂的现实世界任务的不可分割的部分。虽然这些架构从人类大脑中获取灵感，但每种架构都缺少：（

1）学习过程的关键组件——如短期记忆、长期记忆、元记忆、注意当前上下文等（Cowan，2008年）；（2）这些组件如何是相互关联的系统，可以独立运行；和/或（3）积极从数据中学习并记忆过去历史的抽象能力。我们认为，在一个有效的学习范式中，类似于人类大脑，有着独特而相互关联的模块，每个模块负责学习过程中的关键组件。

1.1 记忆视角

记忆是一种基本的心理过程，是人类学习不可分割的组成部分（Terry 2017）。没有正常运作的记忆系统，人类和动物将被限制在基本的反射和刻板行为中。因此，记忆已经成为机器学习文献中许多重要研究的灵感来源；例如，Hopfield网络（Hopfield 1982）、LSTM（Jürgen Schmidhuber和Hochreiter 1997）和Transformer（Vaswani等，2017）。

灵感来自于神经心理学文献中对记忆和学习的常见定义（Okano，Hirano和Balaban 2000），大多数已有的体系结构将记忆视为输入引起的神经更新，并将学习定义为在给定目标的情况下获取有效和有用的记忆的过程。从这个角度来看，循环神经网络（RNNs）（Williams和Zipser 1989）可以定义为具有矢量值记忆模块M（也称为隐藏状态）的模型，其有两个主要步骤：给定时间t的新输入𝑥𝑡，模型（1）使用函数𝑓（M𝑡−1,𝑥𝑡）来更新内存。

(压缩版本)；并使用函数𝑔(M𝑡,𝑥𝑡)检索输入的对应记忆（详见第2.1节）。类似地，Transformer可以被看作是具有不断增长记忆和两个类似步骤的体系结构。也就是说，键和值矩阵对作为模型的记忆，并且模型：(1)通过将键和值追加到记忆中来更新记忆（不压缩），并(2)通过查找查询向量和键向量的相似性来检索查询向量的对应记忆，然后用于权重值向量的输出。

这一观点可以帮助我们更好地理解现有的范式，它们之间的关键区别，并设计更有效的架构。例如，Transformer（Vaswani等人，2017）和线性Transformer（Katharopoulos等人，2020）之间的主要区别在于记忆结构以及记忆更新步骤，其中线性Transformer将历史数据压缩为固定大小的矩阵值记忆，而Transformer在不进行任何压缩的情况下保留所有历史数据（在上下文长度内）。虽然线性Transformer和线性RNN（包括状态空间模型）在记忆更新步骤中都会压缩信息，但关键区别在于记忆的结构。

线性RNN（与线性Transformer相对）使用向量值记忆（与矩阵值记忆相对）。因此，这个观点激励我们提出以下问题：（Q1）什么构成了良好的记忆结构？（Q2）什么是适当的记忆更新机制？和（Q3）什么是良好的记忆检索过程？

重温人类记忆的理解，它既不是一个单一的过程，也不仅仅有一个功能（Cowan 2008）。事实上，记忆是一个由系统组成的联盟-例如，短期记忆，工作记忆和长期记忆-每个系统都有不同的功能和不同的神经结构，并且每个系统都可以独立操作（Willingham 1997） 。这一事实激励我们提出以下问题：（Q4）如何设计一个包含不同连接的记忆模块的高效架构。最后，存储记忆是一个神经过程，需要编码和存储过去的抽象。单纯地假设一个单一的向量或者矩阵足以线性地编码数据来存储长期历史是过于简化的。（Q5）是否需要一个深度记忆模块来有效存储/记住长期历史？

1.2 贡献和路线图

在本文中，我们旨在通过设计一个长期的神经记忆模块来回答上述五个问题，该模块可以在测试时高效有效地学习记忆。在基于其设计的基础上，我们讨论了如何将其融入到架构中。

神经记忆（§3）。我们提出了一种（深度）神经长期记忆，该记忆模块（作为元上下文模型）学会了如何在测试时将数据存储在其参数中。受人类长期记忆系统的启发（Mandler 2014），我们设计了这个记忆模块，使得违背期望的事件（令人惊讶）更易记忆。为此，我们通过神经网络对输入关联记忆损失的梯度来衡量输入的意外性（具体细节见§3.1）。为了更好地处理有限的记忆空间，我们引入了一个衰减机制，考虑到记忆容量与数据意外性之间的比例，以实现更好的记忆管理。我们展示了这种衰减机制实际上是现代递归模型中遗忘机制的泛化（Dao和Gu 2024；Gu和Dao 2024；S. Yang、Kautz和Hatamizadeh 2024）。有趣的是，我们发现这种机制等价于用小批量梯度下降、动量和权重衰减优化元神经网络。基于将小批量梯度下降张量化以使用更多的矩阵乘法运算（Yu Sun等人2024），我们提出了一种快速且可并行化的算法来训练我们的深度神经长期记忆。

Titans架构（§4）。在设计长期神经记忆之后，一个重要的待解决问题是如何将记忆有效且高效地融入深度学习架构中。我们介绍了Titans，一系列由三个超头组成的深度模型：（1）核：该模块包含短期记忆，负责主要的数据处理流程（我们使用有限窗口大小的注意力）；（2）长期记忆：这个分支是我们的神经长期记忆模块，负责存储/回忆长期的过去；（3）持久记忆：这是一组可学习但与日期无关的参数，用于编码关于任务的知识。最后，作为概念验证，我们提出了Titans的三种变体，将记忆作为：（i）上下文，（ii）层，以及（iii）门控分支加入其中。

实验结果（§5）。我们对语言建模、常识推理、回忆密集型、大海捞针、时间序列预测和DNA建模任务进行了实验评估。我们观察到，我们的Titan架构在一系列综合性基准测试中表现优于所有现代递归模型以及它们的混合变体（与滑动窗口注意力相结合）。此外，相比于使用相同上下文窗口的Transformer模型，Titan表现更好，并且与使用全部上下文的Transformer模型具有竞争力。与Transformer相反，Titan模型可以扩展到超过2M的上下文窗口大小。

2 初步工作

在本节中，我们讨论我们在论文中使用的符号和一些背景概念。我们让𝑥 ∈ R𝑁×𝑑in为输入，M为神经网络（神经记忆模块），Q，K，V为注意力机制的查询，键和数值，M为注意力掩码。在对序列进行分段时，我们使用S(𝑖)来指代。

第𝑖段落。在本文中，我们滥用符号，并使用下标来引用矩阵、向量或段的特定元素。例如，我们将S(𝑗𝑖)视为第𝑖段中的第𝑗个Token。唯一的例外是带有𝑡下标的情况，我们保留用于索引时间上的重复，或者神经网络在时间𝑡上的状态。给定一个神经网络N和一个数据样本𝑥，我们使用N (𝑥)（或N∗(𝑥)）来表示带有（或不带有）权重调整的前向传播。同样，我们滥用符号并使用N (𝑘)来引用神经网络的第𝑘层。在接下来的内容中，我们首先讨论注意力及其有效变体的背景，然后回顾现代线性RNN。最后，我们讨论这些架构的记忆视角，这促使我们设计Titans。 （原文没有给出"Titans"的解释，我没有进行翻译）

2.1 背景

注意力。Transformer变压器（Vaswani et al. 2017）作为许多深度学习模型的事实支柱，基于注意力机制。给定输入𝑥 ∈ R𝑁×𝑑in，因果注意力基于输入相关的键、值和查询矩阵上的softmax计算输出y ∈ R𝑁×𝑑in：

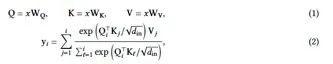
WQ、WK和WV属于可学习参数，它们都是R𝑑in×𝑑in的矩阵。尽管transformers在召回方面具有强大和有效的能力，但是为了计算输出，需要至少𝑁 × 𝑑个运算符，导致更大的内存消耗和对于更长序列的较低吞吐量。

高效的注意力机制。为了改善长序列的softmax注意力在内存消耗和吞吐量方面的问题，各种研究聚焦于注意力的I/O感知实现（Dao 2024; Dao, D. Fu, et al. 2022），通过稀疏化注意力矩阵（B. Chen et al. 2021; Choromanski et al. 2021; Dai et al. 2019）、近似softmax (Arora et al. 2024)，或者开发基于核（线性）的注意力机制（Aksenov et al. 2024; Kacham, Mirrokni, and P. Zhong 2024; Schlag, Irie, and Jürgen Schmidhuber 2021; S. Yang, B. Wang, Shen, et al. 2024）来设计更高效的注意力机制。在本部分中，我们将重点放在后者，即线性注意力机制上，其中标准注意力的softmax被替换为替代的核函数𝜙(., .)，使得𝜙(𝑥,𝑦) = 𝜙(𝑥)𝜙(𝑦)。因此，注意力可以表示为：

导致吞吐量更高，因为术语𝐾𝑗=1 𝜙(𝐾𝑗)和𝐾ℓ=1 𝜙(𝐾ℓ)在每个步骤中被重复使用。当选择内核为单位矩阵时（Yutao Sun等人，2023年），上述表述也可以用递归格式写成：

线性注意力机制可有效支持推理。

现代线性模型及其记忆视角。正如之前讨论的，人们可以将学习定义为获取有效和有用记忆的过程。基于这一点，可以将循环神经网络（RNNs）的隐藏状态视为记忆单元，模型旨在将信息压缩到其中。因此，在一般形式的循环神经网络中，隐藏状态可以被视为记忆单元，循环过程可以拆分为在记忆单元中的读取和写入操作。也就是说，我们让𝑥 ∈ R𝑁×𝑑in表示输入，M ∈ R𝑑表示记忆单元，而y ∈ R𝑑in表示输出，那么循环神经网络的一般形式被定义为：

𝑓(.)是读取函数，𝑔(.)是写入函数。请注意，这里的M𝑡的下标表示时间𝑡时内存的状态。从这个角度来看，线性Transformer的递推公式（见方程4）等同于将键和值（𝐾𝑡,𝑉𝑡）进行加性压缩并写入到矩阵值记忆单元M𝑡中。因此，当处理长上下文数据时，这个加性过程的性质会导致内存溢出，严重影响模型性能。为了解决这个问题，研究集中在两个有前途的方向上：(1)添加遗忘机制：一些研究提出了适应性（数据相关）的遗忘门机制用于线性模型，当需要时能够擦除记忆。作为这类模型的例子，我们提到GLA（S. Yang, B. Wang, Shen等人，2024年）、LRU（Orvieto等人，2023年）、Griffin（De等人，2024年）、xLSTM（Beck等人，2024年）和Mamba2（Dao和Gu，2024年），后者还与传统状态空间模型的离散版本相连（Gu和Dao，2024年）。（2）改进写入操作：为了克服传统递归模型中内存写入操作的加性性质，Widrow和Hoff（1988年）提出了Delta Rule，即在添加记忆（即键值对）之前，模型首先移除它的过去值。为了增强可并行化训练和扩展性，S. Yang, B. Wang, Yu Zhang等人（2024年）提出了一个快速可并行化算法。最近，S. Yang, Kautz和Hatamizadeh（2024年）通过添加遗忘门改进了DeltaNets。

记忆模块。记忆一直是神经网络设计中的核心部分之一（Graves、Wayne和Danihelka 2014年；JH Schmidhuber 1992年；Jürgen Schmidhuber和Hochreiter 1997年；J. Zhang等人2024年）。将线性层视为关键-值（关联）记忆系统的想法可追溯到快速权重程序，其中动态快速程序被整合到递归神经网络中，作为可写内存（JH Schmidhuber 1992年）。希布学习规则（Hebb 2005年）和delta学习规则（Prados和Kak 1989年）是快速权重程序中最流行的学习规则，已在各种研究中进行了广泛探讨（Irie、Schlag等人2021年；Munkhdalai、Sordoni等人2019年；Munkhdalai和H. Yu 2017年；Schlag、Irie和Jürgen Schmidhuber 2021年；JH Schmidhuber 1992年；S. Yang、Kautz和Hatamizadeh 2024年；S. Yang、B. Wang、Yu Zhang等人2024年）。然而，所有这些模型都基于瞬时惊喜，缺乏序列中的Token流动（参见第3.1节），并且大多数模型缺乏遗忘门，导致内存管理不佳。

我们在附录C中进一步讨论了我们的架构与最近模型之间的联系。附录A中还讨论了其他相关工作。

3  学习如何在测试时记忆

为了克服长期记忆的缺乏并使模型能够学习、遗忘和检索信息，在本节中，我们提出了一个神经长期记忆模块，它是一个在测试时学会记忆的元模型。在3.1节中，我们首先讨论了神经记忆的动机和设计。在3.2节中，我们讨论了我们的架构设计如何受益于快速且可并行化的训练。最后，在3.3节中，我们使用持久记忆模块增强了我们的架构，其中我们使用可学习但与数据无关的参数来学习任务的元信息。

3.1 长期记忆

设计神经长期记忆模块时，我们需要一个能够将过去历史的抽象编码到其参数中的模型。一个例子是已经被证明能够记住其训练数据的LLM模型（Leybzon和Kervadec，2024；Schwarzschild等，2024；Staab等，2024）。因此，一个简单的想法是训练一个神经网络，并期望它能够记住其训练数据。然而，记忆几乎一直被认为是神经网络中不期望出现的现象，因为它限制了模型的泛化能力（Bayat等，2024），引起了隐私方面的担忧（Staab等，2024），从而导致在测试时性能不佳。此外，训练数据的记忆在测试时可能并没有帮助，因为数据可能是来自分布之外的。我们认为，我们需要一个在线元模型，在测试时学习如何记住/忘记数据。在这种设置下，模型正在学习一种能够进行记忆的函数，但它没有过度适应训练数据，在测试时表现出更好的泛化能力。

学习过程和惊奇度量。训练长期记忆的关键思想是将其训练视为在线学习问题，在其中我们的目标是将过去的信息𝑥1, . . . ,𝑥𝑡−1压缩成我们的长期神经记忆模块M𝑡的参数。如前所述，对于违背期望的事件（即令人惊讶的事件）人类更容易记住（Mandler 2014）。受此启发，模型的惊奇度可以简单定义为其相对于输入的梯度。梯度越大，输入数据与过去数据的差异就越大。因此，使用这个惊奇度分数，我们可以更新记忆为：

这种惊喜指标可能导致错过在一个重大惊喜时刻之后出现的重要信息。也就是说，在经历了几个令人惊喜的步骤之后，梯度可能变得极小，导致停留在一个平坦区域（即局部最小值），并且错过了序列中的某些部分的信息。从人类记忆的角度来看，一个事件在很长一段时间内可能不会始终让我们感到惊讶，尽管它是令人难忘的。原因是最初的瞬间足够惊喜，从而在很长的时间范围内引起我们的注意，导致我们记住了整个时间范围。为了改进上述惊喜指标（方程式8），我们将惊喜指标分为（1）过去的惊喜，用于衡量最近过去的惊喜量；和（2）瞬时惊喜，用于衡量即将到来数据的惊喜量。

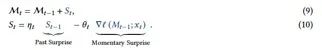
过去的惊奇|{z}瞬间的惊奇  𝑆𝑡

有趣的是，这个公式与具有动量的梯度下降类似，其中动量元素在哪里。因此，在这个公式中，动量充当跨时间（序列长度）的惊喜记忆。在这个公式中，项𝜂𝑡是一个数据相关的惊喜衰减（𝑥𝑡的函数），控制着随时间衰减的惊喜程度，而项𝜃𝑡则控制着多少瞬时惊喜应以数据相关的方式纳入最终的惊喜度量中。这种数据依赖性在这个设计中特别重要：虽然以前的标记的惊喜可能需要影响下一个标记的惊喜，但只有当所有标记都是相关的并且处于相同的上下文中时才有效。因此，数据相关的𝜂可以控制记忆是否需要: (1)通过设置𝜂𝑡 → 0忽略上次的惊喜（可能是由于上下文的变化），或者(2)通过设置𝜂𝑡 → 1全部纳入上次的惊喜（可能是因为该标记与其最近的过去标记高度相关）。

我们的目标。我们上述的惊喜度量基于损失函数ℓ(.; .)，这是我们的记忆在测试时学习行动的目标。也就是说，我们的记忆模块是一个元模型，它基于损失函数ℓ(.; .)学习一个函数。

在这项工作中，我们关注关联记忆，我们的目标是将过去的数据存储为键和值对。给定𝑥𝑡，类似于Transformers（Vaswani等人，2017年），我们使用两个线性层将𝑥𝑡投影为一个键和一个值：

其中WK和WV ∈ Rdin×din。接下来，我们希望我们的memory模块能够学习key和values之间的关联。为此，我们将损失定义如下：  我们希望我们的记忆模块学习键与值之间的关联。为此，我们定义损失如下：

通过在我们的元模型（内存）的内循环中优化上述损失函数，模型学习如何在测试时记忆键和值之间的映射。注意，类似于元学习模型（Nichol 2018; Zintgraf et al.）。  Note: The translation has been provided in the original text, no translation is needed.

2019年，内循环中进行了记忆的训练，因此上述损失函数中的参数𝑊𝐾和𝑊𝑉是超参数。因此，在内循环中，我们优化M的权重，而在外循环中，我们优化整个架构的其他参数。

遗忘机制。在处理非常大的序列时（例如，数百万个标记），管理应该遗忘哪些过去的信息是至关重要的，即使有一个深度或非常大的矩阵值内存也是如此。为此，我们使用了一种自适应遗忘机制，使得内存可以遗忘不再需要的信息，以更好地管理内存的有限容量。也就是说，给定下一个标记𝑥𝑡，我们将更新规则修改为：

𝛼𝑡 ∈ [0, 1]是灵活控制记忆的门控机制，即决定应该忘记多少信息。例如，它可以通过𝛼𝑡 → 0更新记忆而不影响过去的抽象，也可以通过𝛼𝑡 → 1清空整个记忆。在本节后面，我们将展示这种权重衰减机制与现代循环神经网络中的门控机制（Dao and Gu 2024; Orvieto et al. 2023）密切相关。

记忆架构。在这篇论文中，我们将简单的MLP（多层感知器）作为我们长期记忆的架构，主要原因是我们想更好地激发长期记忆设计的动机以及将其融入架构的方式。然而，我们的公式和架构设计开辟了设计神经架构以更有效和高效地记忆数据的新研究方向。最近，已经有一系列有希望的工作来设计这样的架构（Berges等人，2024年；Cetin等人，2024年；J. Zhang等人，2024年），将它们融入我们的框架（即，用这些架构替换简单的MLP）可能是一个有趣的未来工作。

当使用向量值或矩阵值的存储器（De等人，2024年; Orvieto等人，2023年; S. Yang，B. Wang，Shen等人，2024年）时，存储器模块会将过去的数据进行压缩，并将其适应到一条线上。也就是说，从元学习或在线学习的角度来看（Yu Sun等人，2024年），使用矩阵值存储器M = 𝑊 ∈ R𝑑in×𝑑in等效于优化ℓ(𝑊𝑡−1;𝑥𝑡) = ∥𝑊𝑡−1k𝑡 − v𝑡 ∥22，这是一个在线线性回归目标，因此最优解假设历史数据之间的依赖关系是线性的。 另一方面，我们提出，深度存储器模块（即。。。）

在理论结果上与至少包含两层的MLP严格比线性模型更具表现力（Hornik, Stinchcombe, and White 1989）一致，我们在第5.5节中展示深度记忆模块在实践中更加有效。

在上文中，我们讨论了如何设计和训练一个长期记忆模块，该模块在测试时学习记忆。一个关键的问题是：如何从记忆中检索信息？我们仅使用前向传播而不进行权重更新（即推断）来检索一个与查询对应的记忆。形式上，给定一个输入。

在这里，我们使用线性层𝑊𝑄来投影输入，即，q𝑡 = 𝑥𝑡𝑊𝑄，并通过以下方式从记忆𝑦𝑡中检索相应（或有用的）信息：

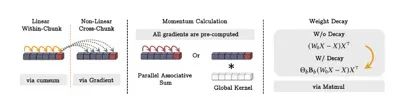
图1：神经记忆训练可以在并行和使用矩阵乘法的情况下进行。

3.2     如何并行化长期记忆训练

如上所述，我们的长期记忆模块的设计相当于通过优化联想记忆损失函数ℓ(M𝑡−1;𝑥𝑡) = ∥M𝑡−1 (k𝑡) − v𝑡 ∥22来训练元模型，其中使用了动量和权重衰减的梯度下降法。因此，理论上，长期记忆模块的训练需要O(𝑁)个浮点运算操作，其中𝑁为序列长度。然而，实际上，我们需要并行化训练过程，并充分利用硬件加速器（如TPUs、GPUs），我们需要将过程张量化并使用更多的矩阵乘积运算。

接下来，我们将展示通过使用小批量梯度下降、数据相关的学习率和权重衰减来计算内部循环中的权重，可以进行重新构建，只使用矩阵乘法和求和运算。我们基于Yu Sun等人（2024年）的工作进行了改进，该工作显示了使用小批量梯度下降（具有恒定学习率）优化模型的前向传播可以使用矩阵乘法计算。我们可以将序列分割成大小为𝑏 ≥ 1的块，并将小批量梯度下降写成以下形式：

其中，𝑡' = 𝑡 − mod(𝑡,𝑏)，而𝛽𝑖 = Î𝑖𝑗=1(1 − 𝛼𝑗)。为了简单起见，我们关注第一个块，即𝑡 = 𝑏，因此𝑡' = 0。此外，我们说明了当M𝑡 = 𝑊𝑡是线性时的过程。具有𝑁𝑝 ≥ 2的MLPs的过程类似。使用我们的损失函数，我们有：

𝑖=1𝛽𝑖的中文翻译为𝑖=1𝛽𝑖。

Θ𝑏 =diag 𝜃1 𝜃2 . . . 𝜃𝑏和B𝑏在𝛽𝛽𝑏𝑖上被类似地定义。注意，我们不需要为𝑘 = 1, . . . , 𝑁 /𝑏存储所有Θ𝑘𝑏和B𝑘𝑏，而是为每个块存储这些矩阵，从而使用更少的内存。接下来，我们扩展这个表示，以便我们也可以包含动量项。在带有动量的分块梯度下降中，如果我们考虑动量项，我们有：

𝑢𝑡 = ∇ℓ (𝑀𝑡′;𝑥𝑡)。注意，我们可以同时计算所有𝑢𝑡，因此方程18是一个具有𝑢𝑡作为输入、𝑆𝑡作为隐藏状态和𝜂𝑡作为输入相关转换值的线性递归。因此，我们可以使用并行的关联扫描（J.T. Smith, Warrington和Linderman 2023）来计算此块中的𝑆𝑡s。

参数作为块的函数。我们可以将参数𝛼𝑡，𝜃𝑡和𝜂𝑡设置为其块的函数，而不是使其依赖于输入（即使其为Token𝑥𝑡的函数）。尽管失去了一定的表达能力，但这种形式可以帮助加快训练速度。在这种情况下，我们在每个块中使用相同的𝛼，𝜃和𝜂值。因此，在方程17中，我们可以使用单一标量来存储Θ。同样，在方程18中我们也可以加快运算速度。也就是说，当𝜂和𝜃在每个块内是可学习但时间不变的时候，该方程变成了一个线性时不变系统（LTI），可以通过全局卷积来计算（Gu，Goel和Re 2022）。在我们的实验中，我们将这些参数设置为Token的函数。然而，这种简化（即作为块的函数）可以成为未来以更高效的方式训练更大模型的研究兴趣所在。

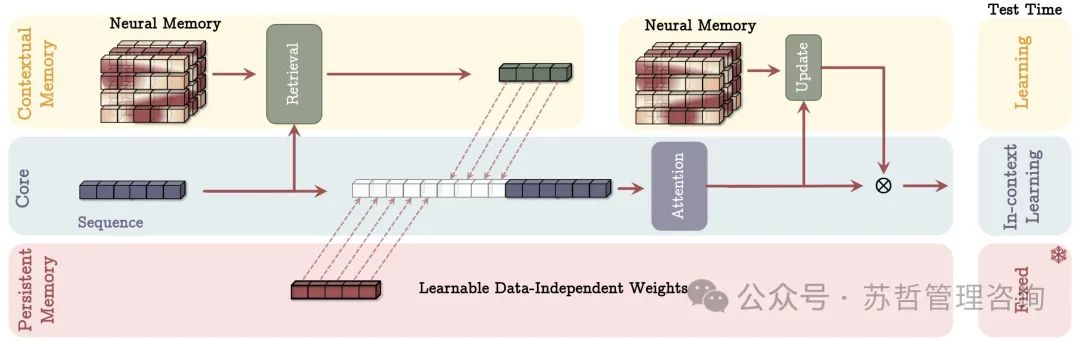
图2：内存作为上下文（MAC）架构。该架构包括三个分支：（1）核心，（2）上下文。

长期记忆（long-term memory），以及持久记忆（persistent memory）。核心分支将相应的长期记忆和持久记忆与输入序列连接起来。接下来，注意力在序列上进行操作，并决定哪部分信息应存储在长期记忆中。在测试时，与上下文记忆相关的参数仍在学习中，与核心分支相关的参数负责上下文内的学习，而持久记忆的参数负责存储关于任务的知识并且是固定的。

3.3 持久性内存

我们的长期记忆也可以被视为上下文记忆，这意味着输出完全取决于上下文。因此，除了我们的长期记忆外，我们还使用一组可学习但与输入无关的参数作为任务相关的记忆。这种类型的记忆在文献中被称为持久性或元记忆（X. Dong等，2024年；Sukhbaatar，Grave等，2019年）。给定𝑁𝑝≥1，我们使用可学习的参数𝑃=𝑝1 𝑝2 ...𝑝𝑁𝑝，并将其附加到我们序列的开头：即，给定一个上下文窗口大小为𝑁，我们将输入修改为：

其中||表示连接。接下来，我们从三个方面讨论了持久性内存的动机：

记忆视角。正如前面讨论过的，我们的神经长期记忆是一种上下文记忆，其中所有参数都是依赖于输入的。然而，一个有效的记忆系统还需要输入无关的参数来存储任务知识的抽象。也就是说，掌握一个任务需要记忆如何完成任务的知识，而这些参数负责存储这样的知识。

前馈网络视角。在Transformer架构中，注意力模块之后是全连接层，据显示这些层类似于注意力权重，但具有数据无关的参数。也就是说，Sukhbaatar、Grave等人（2019年）表明，将全连接层中的ReLU替换为Softmax会产生类似注意力权重的结果，其中权重是数据无关的：

实际上，当𝑊𝐾和𝑊𝑉与𝐾和𝑉矩阵在注意力模块中作为输入无关时，它们的作用类似于𝐾和𝑉矩阵。希望持久的记忆权重具有相同的功能，这意味着在序列的第一部分使用它们将导致具有输入无关的注意力权重（Sukhbaatar, Grave等，2019年）。

技术观点。带有因果掩膜的注意力对序列中的初始标记具有隐式偏见，因此注意力权重几乎总是对初始标记高度活跃，导致性能下降。从技术角度来看，序列开始处的这些可学习参数可以通过更有效地重新分配注意力权重来减轻这种影响（Han等，2024年；Xiao等，2024年）。

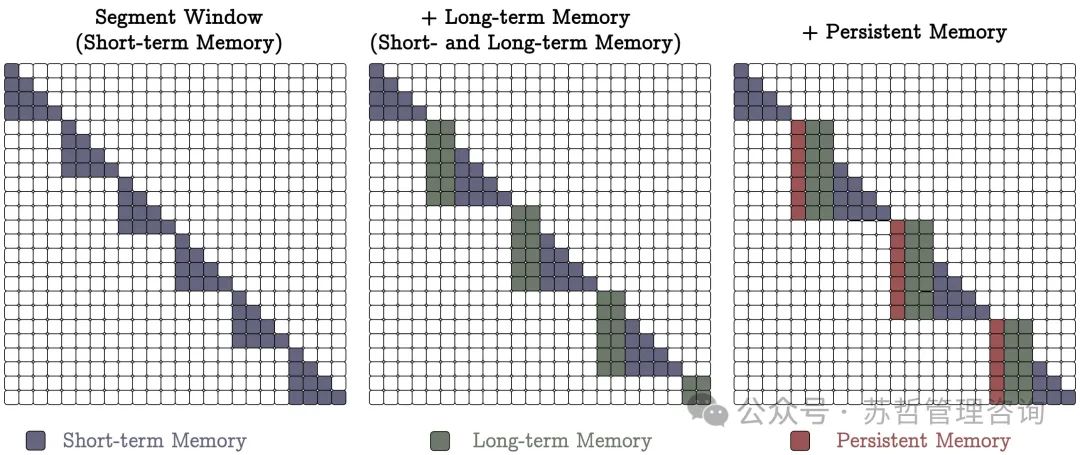
记忆作为上下文（MAC）。我们将序列分割并在每个窗口中使用全因果注意力。再次，第一

𝑁𝑝 tokens是持久性内存，下一个𝑁𝑙是长期记忆tokens。

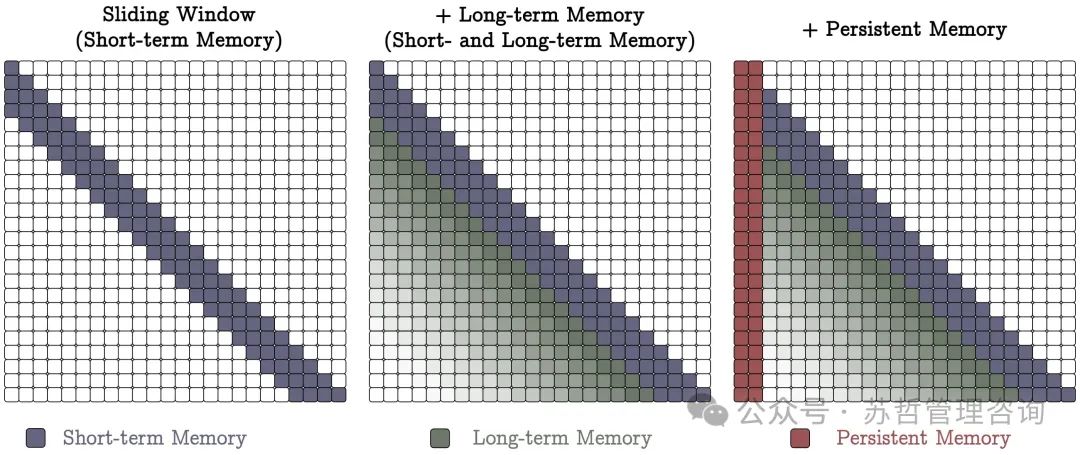
内存作为门控（MAG）。我们使用滑动窗口注意力（SWA）作为短期记忆，我们的神经记忆模块作为长期记忆，通过门控结合在一起。

图3：不同类型的泰坦的注意力蒙版。

4 如何融入记忆？

一个至今未解答的重要问题是：如何将设计的神经记忆有效而高效地融入到深度学习结构中？正如前文所讨论的，从记忆的角度来看，transformers中的K和V矩阵可以被解释为一个联想记忆模块。由于它们对依赖关系的准确建模以及有限的上下文窗口，我们将其解释为短期记忆模块，关注当前的上下文窗口大小。另一方面，我们的神经记忆能够不断学习来自数据并将其存储在权重中，能够扮演长期记忆的角色。在本节中，我们旨在通过提出Titans的三个不同变体来回答上述问题。在我们的实验证明中，我们展示了每个变体都具有自己的优点/缺点，并且在非常长的上下文中也可以在效率和效果之间实现权衡。

4.1 记忆作为背景

在第一种架构设计中（见图2），我们将内存视为当前信息的上下文。也就是说，给定一个长序列𝑥 ∈ R𝑁×𝑑in，我们首先将序列分成固定大小的段S(𝑖)，其中𝑖 = 1, . . . , 𝑁 /𝐶。给定传入的段落S(𝑡)，我们将其视为当前上下文和其以前的段落视为历史信息。因此，让M𝑡−1代表段落S(𝑡)之前的长期记忆状态，我们将输入的上下文作为查询用于从长期记忆M𝑡−1中检索相应的信息。也就是说，我们检索与S(𝑡)对应的过去信息为：

q𝑡 =S(𝑡)𝑊𝑄。接下来，我们将使用这些历史信息以及我们持久性内存参数作为输入序列传递给注意力模块。

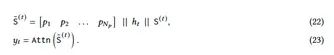
整个序列上的注意力图结构如图3a所示。然后我们使用𝑦𝑡来更新下一个片段和最终输出的长期记忆模块：

在上述过程中，请注意，我们通过前向传播来更新M𝑡−1的权重。

这种架构有两个关键优势：(1)注意力机制结合历史和当前上下文，能够决定在给定当前数据时是否需要长期记忆的信息。(2)注意力模块有助于

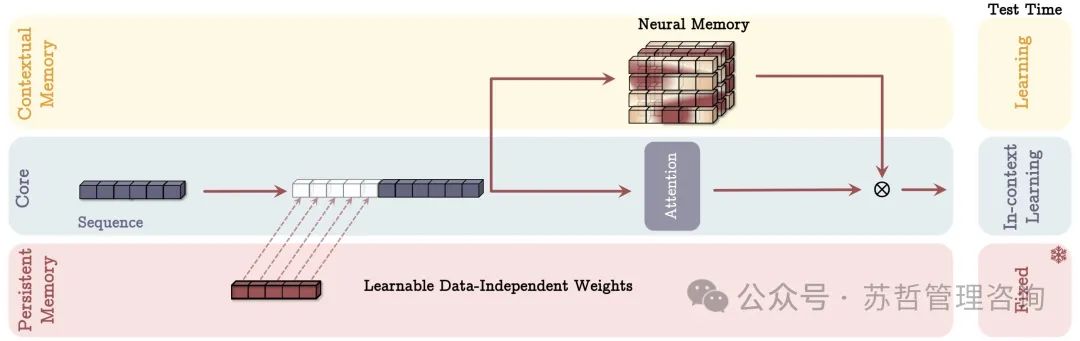
图4：记忆作为门（MAG）架构。这个架构同样由（1）核心、（2）语境记忆和（3）持久记忆三个分支组成。然而，它仅将持久记忆纳入上下文，并使用一个门控机制将记忆与核心分支结合起来。在测试时，行为与图2相同。

长期记忆只能存储来自当前上下文的有用信息。也就是说，每个片段中并不是所有的标记都是有用的，而且记住所有标记可能导致内存溢出。因此，注意机制帮助记忆理解哪些信息是有用的，更好地管理内存容量。（3）在测试时：（i）持久性记忆参数是固定的，因为它们编码了关于任务的知识，不应该更改；（ii）注意模块的权重是上下文学习器；（iii）长期记忆模块仍在学习（记忆）测试时的信息。也就是说，我们甚至在测试时更新神经记忆的权重，因为这些权重编码了很长时间的抽象信息。

4.2 门控记忆

在下一个变体中（见图4），在一个分支中，我们直接使用输入数据来更新长期记忆，在第二个分支中，我们使用滑动窗口注意力（SWA）：

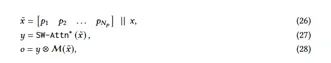
滑动窗口注意力机制带有前缀，记作SW-Attn∗(参见图3b)。需要注意的是，与以前的设计不同，我们不再对输入数据进行分段。同时，我们滥用符号并使用M(𝑥)来指代序列中所有Token递归完成后记忆的最终输出。在上述方程中，⊗可以是任何非线性门控操作。在我们的实验中，

我们使用可学习的矢量值权重来对输出𝑦和M(𝑥˜)进行归一化，然后接着使用非线性函数𝜎(.)。

这个设计的整体关注掩码在图3b中显示。在这个设计中，滑动窗口注意力作为精确的短期记忆，而神经记忆模块作为模型的衰减记忆。这种架构设计也可以看作是一个多头架构，其中头部的结构不同（X. Dong等人，2024年）。

4.3  内存作为一层

最后一种变体使用深度神经网络的神经内存层（Memory As a Layer，MAL）（见图5）。这种架构设计在文献中更为常见，其中混合模型将递归模型与完全或滑动窗口的注意力机制相叠加。给定输入𝑥，我们有：

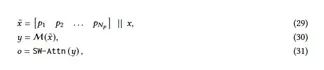
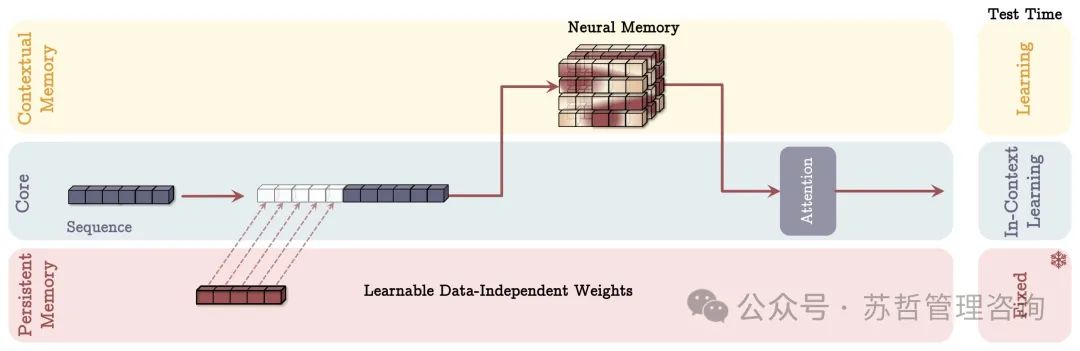
图5：内存作为一层（MAL）架构。在这种架构中，内存层负责在注意力模块之前压缩过去和当前的上下文。

SW-Attn表示滑动窗口注意力。这种设计的主要缺点是模型的能力受到每个层的限制，因此无法利用注意力和神经记忆模块的互补数据处理优势。在我们的实验中，为了评估这种设计中的记忆，我们使用了类似H3（D. Y. Fu等人，2023年）的架构，其中我们用我们的神经记忆模块（LMM）替换了序列模型。

记忆无需注意力。尽管在上面我们讨论了MAL作为LMM和注意力的顺序组合，但MAL的一个简单变体是将LMM作为一个没有任何注意力的序列模型。从记忆的角度来看，就像我们在第一节中讨论的那样，我们期望记忆系统的每个部分都能独立工作，即使其他组件受到干扰。因此，即使没有短期记忆（即注意力），长期记忆模块仍然应该是一个强大的模型。在我们的实验证明中，我们将这种变体称为LMM或Titans（LMM）。关于Titans和其他现代循环模型的连接，我们在附录C中提供了额外的讨论。

4.4 架构细节

为了简化和展示的目的，我们避免讨论实现细节，比如使用残差连接、线性层门控和归一化。在所有块中，我们使用残差连接。在我们的实现中，我们使用SiLU(.)激活（Elfwing, Uchibe和Doya 2018）作为计算查询、键和值的非线性激活函数，并使用ℓ2范数对查询和键进行归一化。

卷积。在最近的现代线性循环模型（Gu和Dao 2024; S. Yang，Kautz和Hatamizadeh 2024）之后，我们在每个查询、键和值投影后都加入了1D的深度可分离卷积层。尽管对性能影响不大，但这些1D卷积已经显示出性能的提升，并且计算效率也很高。

门控。我们还遵循最近使用归一化和门控的架构，该架构在最终的输出投影之前使用线性层（Mehta等人，2023年）。

定理4.1.与变压器、对角线线性递归模型和DeltaNet相反，它们都限于TC0（Merrill，Petty和Sabharwal 2024），泰坦能够解决超出TC 0范围的问题，这意味着泰坦在状态跟踪任务中理论上比变压器和大多数现代线性递归模型更具表达能力。

5 实验

接下来，我们评估Titans及其变体在语言建模、常识推理、大海捞针、DNA建模和时间序列预测任务中的表现。更详细地，在本节中，我们回答以下实证问题：（1）相对于基线，在下游任务中Titans的表现如何？（见§5.2、§5.6和§5.7）；（2）Titans的实际上下文长度是多少？（见§5.3和§5.4）；（3）Titans在上下文长度方面如何扩展？（见§5.8）；（4）记忆深度如何影响性能和效率？（见§5.5）；以及（5）Titans的每个组件在其性能中的贡献是什么？（见§5.9）。

5.1 实验设置

模型。在我们的实验中，我们关注的是Titans的三个变种，我们将其称为：带有（1）内存作为上下文（MAC）的Titans，（2）带有内存作为门（MAG）的Titans，以及（3）带有内存作为层（MAL）的Titans，以及（4）仅有神经内存模块。我们将长期记忆作为一个独立的模块使用的原因是基于我们对学习的定义。正如在第1节中讨论的那样，我们将学习定义为获取有效和有用的记忆的过程。因此，我们期望我们的长期记忆能够在没有注意力的情况下从数据中有效地学习。对于这些模型的每一个，我们考虑了四个不同的规模：（i）170M，（ii）340M，（iii）400M和（iv）760M参数。前三个模型是使用从FineWeb-Edu数据集（Penedo等人，2024年）采样的15B个Token进行训练，而最后一个模型则是使用来自同一数据集的30B个Token进行训练。

基准。我们将我们的模型与最先进的线性循环模型、变压器模型和混合模型进行比较。

(recurrent + attention)更具体地说，在语言任务中，我们与Transformer++ (Touvron et al. 2023)进行了比较。

RetNet（孙宇涛等，2023年）、门控线性注意力（GLA）（杨帅、王斌、沈等，2024年）、Mamba（顾道，2024年）、Mamba2（道和顾，2024年）、DeltaNet（杨帅、王斌、张宇等，2024年）、TTT（孙宇等，2024年）和门控DeltaNet（杨帅、考茨和哈塔米扎德，2024年）。在海量数据中寻找少量关键数据的任务中，我们还与GPT4（Achiam等，2023年）、Llama3与RAG（Touvron等，2023年）、RecurrentGemma2-9B（Botev等，2024年）和Mistral（姜等，2023年）模型进行了比较，这些模型都包含在基准测试中（Yuri Kuratov等，2024年）。在时间序列任务中，我们与基于Mamba的模型（Behrouz、Santacatterina和Zabih，2024年）、基于Transformer的模型（刘扬等，2023年；聂等，2022年；张云豪和闫，2023年）和线性模型（Das等，2023年；李等，2023年；吴等，2023年；曾等，2023年）进行比较。

在训练中，我们遵循了S. Yang，Kautz和Hatamizadeh（2024）的培训程序，并使用了32K的LLama 2分词器，训练长度为4K个标记。我们采用了学习率为4𝑒-4的AdamW优化器，采用余弦退火调度，批量大小为0.5M标记，权重衰减为0.1。

5.2语言建模

我们首先关注语言建模和常识推理任务中的困惑。表1报告了Titans'变体以及基线模型，分别采用340M、400M和760M三种不同规模的结果。在不涉及混合模型的情况下，包括Transformer++在内，我们的神经记忆模块在困惑度和准确性方面表现最佳。将我们的神经记忆模块与TTT进行比较，后者也是基于梯度的递归模型，可以展示出我们的权重衰减以及动量的重要性。正如前面讨论的那样，权重衰减可以被解释为一种门控机制，用于在需要时遗忘过去的数据。此外，动量可以通过为惊喜度量提供额外的存储器来帮助我们更好地管理记忆。虽然一些基线模型也利用了门控机制，例如Mamba、Mamba2和Gated DeltaNet，但我们的神经记忆模块的卓越性能表明了惊喜机制和具有深度和非线性记忆的重要性。我们在5.5节进一步讨论后者。

比较混合模型，我们发现Titan的三种变体（MAC，MAG和MAL）胜过Samba（Mamba + attention）和Gated DeltaNet-H2（Gated DeltaNet + attention）。我们将Titan（MAL）的优越性能归因于神经记忆模块的强大，因为其架构设计和使用的注意力模块都是相同的。比较Titan（MAG）和（MAC），我们发现虽然它们的性能相近，但MAC在处理数据中更长依赖性时表现更好。有趣的是，MAG和MAC都胜过MAL变体，由于它们使用相同的模块，我们将这归因于这些模型的架构设计。这一发现尤为重要，因为文献中目前的混合模型（除了Hymba（X. Dong等，2024年））都使用MAL风格的循环模型和注意力的组合。

5.3 大海捞针

将模型扩展到更长的上下文窗口并不总是等效于对于非常长的序列有效（Hsieh等，2024年）。针对大海捞针（NIAH）任务旨在衡量模型的实际有效上下文长度。在这个任务中，我们评估模型在从长的干扰文本中检索信息（即“针”）方面的表现（即，表1：Titans和基于递归和Transformer的基准在语言建模和常识推理任务上的性能。混合模型用∗标记。简单和混合模型中的最佳结果已突出显示）。

在这部分中，我们使用来自RULER基准的单一NIAH（S-NIAH）任务（Hsieh等，2024），并在长度为2K、4K、8K和16K的序列上评估Titans和基线模型。结果报告于表2中。神经记忆模块在所有三个任务中相对于基线模型取得了最好的结果。我们将这种卓越的性能归因于Titans与现有序列模型的三个关键差异：（1）与TTT相比，我们的神经记忆可以通过使用动量和遗忘机制（即权重衰减）更好地处理内存容量。因此，随着序列长度的增加，神经记忆的性能不会下降，呈现一致的趋势；（2）与具有门控（遗忘）机制的Mamba2相比，Titans具有深层非线性记忆，从而实现更好的内存管理。另外，与我们的神经记忆和DeltaNet不同，Mamba2无法删除记忆，因此表2：Titans和基线模型在RULER基准的S-NIAH任务上的性能。在简单模型和混合模型中，最佳结果已经被突出显示。

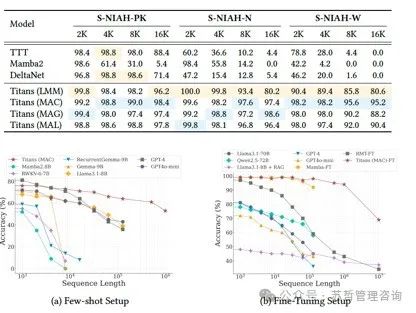
图6：Titans在BABILong基准测试中的表现。Titans（MAC）胜过所有基准模型，包括极其庞大的模型，例如GPT4。

我们可以看到，在增加序列长度时，性能明显下降；(3)与DeltaNet相比，虽然它能够使用增量规则去除记忆，但它无法抹去记忆，缺乏遗忘机制。最后，如预期所见，当使用Titans变种时，我们可以看到与MAC对应的最好结果相当或更好。

5.4 BABILong基准测试

在前一节中，我们讨论了一个简单的NIAH任务的结果，其中需要检索一个单独的针头。尽管Titans相比基准表现更好，但它们在非常长的序列上的优势仍然被隐藏起来。为此，在本节中，我们使用了来自BABILong基准测试（Yuri Kuratov等人，2024年）的一个更难的任务，其中模型需要在极长的文档中推理出分布的事实。我们遵循基准测试中的原始实验设置和训练过程。有两个设置：(1)少样本设置，我们使用大型预训练模型；(2)微调设置，我们微调Titans的MAC变体，以便与其他微调基线进行比较。少样本设置的结果报告在图6a中。在这个设置中，我们可以看到Titans胜过所有其他基线，例如Mamba2.8B（Gu and Dao 2024），RWKV-6-7B（Peng，Goldstein等人，2024年），RecurrentGemma-9B（Botev等人，2024年），Gemma-9B（Team等人，2024年），Llama3.1-8B（Touvron等人，2023年），GPT-4和GPT4o-mini（Achiam等人，2023年）。这些结果是在Titans（MAC）的参数数量远少于基线的情况下取得的。

在微调设置中，我们将Titans的小规模微调版本（MAC）与以下进行比较：（i）像Mamba（Gu和Dao 2024）、RMT（Bulatov，Yury Kuratov和Burtsev 2022）这样的具有几乎与Titans相同参数数量的小模型的微调版本；（ii）带有检索增强生成（RAG）的大模型，例如Llama3.18B（Touvron等人2023）；以及（iii）像GPT-4（Achiam等人2023）、GPT4o-mini、Qwen2.5-72B（A. Yang等人2024）和Llama3.1-70B（Touvron等人2023）这样的极大模型。基准结果由（Yuri Kuratov等人2024）报告。Titans和基准的结果在图6b中报告。Titans胜过所有模型，甚至胜过像GPT4这样的极大模型。此外，与基于Transformer的带有记忆模型（如RMT）相比，Titans显示出更好的性能，主要是由于其强大的内存。也就是说，RMT将历史数据压缩为16大小的矢量值内存，而Titans具有上下文在线内存学习器，能够将过去编码到模型的参数中。有趣的是，即使是

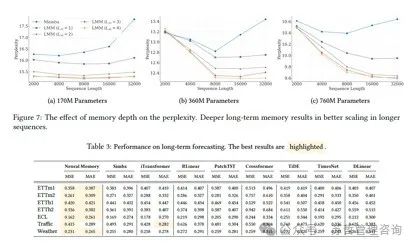
(a) 170M参数(b) 360M参数(c) 760M参数

图7：记忆深度对困惑度的影响。更深的长期记忆有利于更长序列的扩展。

表3：长期预测的表现。最佳结果已经突出显示。

Llama3.1-8B模型与RAG相比，在参数减少了约70倍的情况下表现更差。

5.5 深度记忆的效应

在本节中，我们评估了深度记忆在墙钟训练时间和模型性能方面的影响。为此，我们专注于我们神经记忆模块的不同变体，其中𝐿M = 1, 2, 3, 4。我们还将Mamba作为模型性能的基准。为了公平比较，我们对所有模型使用相同的训练过程，并在Pile数据集的子集上进行训练（L.Gao等人，2020年）。

我们报告了我们模型和基线的困惑度作为序列长度的函数在图7中。有趣的是，随着记忆深度𝐿M的增加，模型可以在所有序列长度上实现更好的困惑度。此外，当模型参数较少时，更深的记忆模块对序列长度更具鲁棒性。随着参数数量的增加，所有模型在较长序列上表现更好。我们还评估了记忆深度（𝐿M=1, 2, 3, 4）对训练吞吐量的影响。我们将训练吞吐量（每秒标记数）作为序列长度的函数报告在图8中。所有模型相对于上下文长度呈线性缩放（即，每秒标记数相对于序列长度保持不变的趋势）。此外，通过增加记忆深度，就像预期的那样，我们可以看到一个更深的内存导致训练速度变慢的线性趋势。因此，不总是高效使用更深的记忆模块，显示出效果和效率之间的权衡。

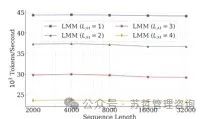
图8：记忆深度对的影响。

5.6 时间序列预测训练吞吐量

为了展示我们的内存模块在更广泛任务中的有效性，我们还评估了其在时间序列预测任务中的性能。为此，我们使用Simba框架（Patro和Agneeswaran 2024）进行时间序列预测，并使用表4：在GenomicsBenchmarks上对预训练DNA模型进行下游评估（Grešová等人，2023）。我们报告了top-1分类准确率（％）。

用我们的神经记忆模块替换其Mamba模块。我们在常见的时间序列预测基准数据集上报告结果- ETT、ECL、Traffic和Weather（H. Zhou等，2021）。结果如表3所示。我们的神经记忆模块表现优异，超越了所有基线模型，包括基于Mamba、线性和Transformer结构的模型。

5.7 DNA建模

为了了解超越自然语言的Titans的能力，我们进一步评估了我们的神经记忆模块在DNA建模任务中的性能。为此，我们在GenomicsBenchmarks（Grešová等人，2023年）的下游任务上评估预训练模型。我们采用了Nguyen等人（2024年）的相同实验设置，并重复使用了Arora等人（2024年）报道的基线结果。Titans（LMM）和基线的性能如表4所示。我们发现LMM在不同的下游基因组学任务中与最先进的架构相竞争任务。

5.8  效率

在这部分中，我们将我们的神经记忆与Titans与最先进的序列模型的效率进行比较。模型对于不同序列长度×批量大小的训练吞吐量在图9中报告。比较循环模型，包括我们的神经记忆模块，我们可以看到我们的记忆模块略慢于Mamba2和门控DeltaNet，主要原因是：(1)具有深度记忆和更具表现力的过渡过程（记忆更新），以及(2)在Mamba2实现中高度优化的内核。有趣的是，Titans (MAL)比基线以及记忆模块更快。这种更好的吞吐量的主要原因是Titans中FlashAttention (Dao 2024)的高度优化内核，用于实现SWA和全注意力模块。

5.9 消融研究

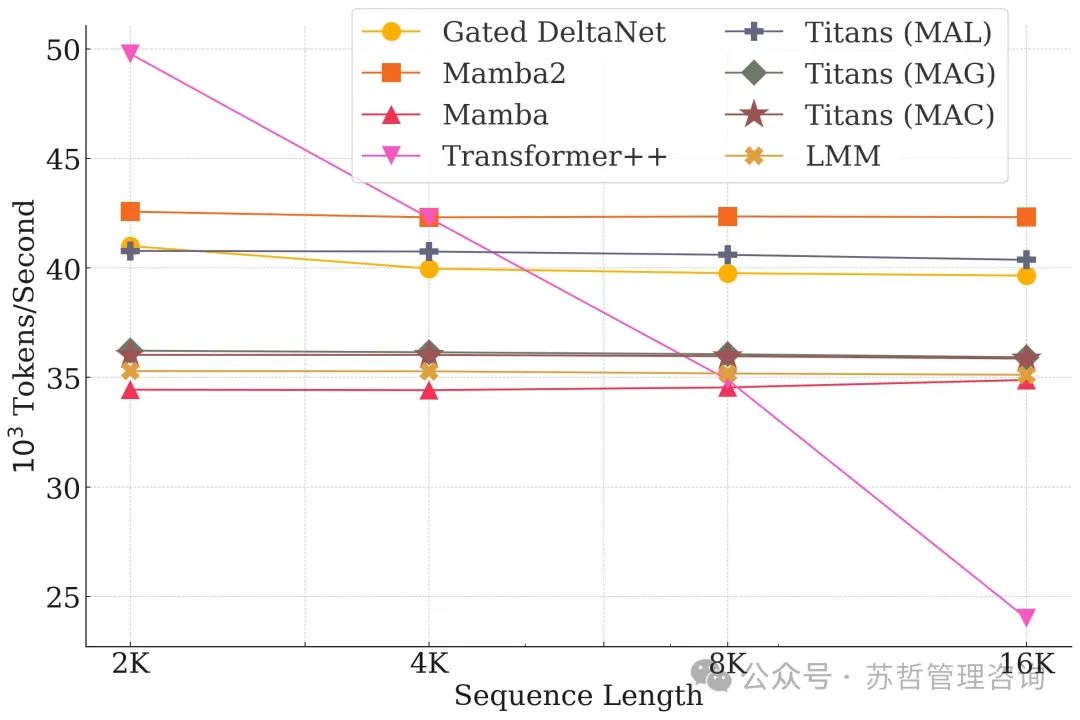
图9：Titans和基线模型的训练吞吐量比较。

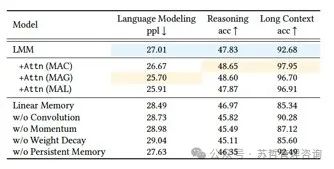
最后，我们对Titans中的不同架构选择进行消融实验。我们将神经记忆模块作为基础模型，然后逐个更改一个组件：(1)将深度记忆替换为线性记忆，删除(2)卷积，(3)惊喜度量中的动量，(4)权重衰减（或遗忘机制），以及(5)持久记忆。结果见表5。神经记忆设计的所有组件都对性能有积极贡献，其中最大的贡献分别来自于权重衰减、动量、卷积和持久记忆。

架构设计的影响。为了评估建筑设计的效果，我们比较了三种Titans的表现，分别在语言建模、常识推理和长上下文NIAH（BABILong）任务三个方面。结果见表5。我们发现MAC和MAG在语言建模和常识推理任务上表现接近，而MAC在长上下文NIAH任务中表现显著优于MAG。这两种模型均比MAL表现更好。这些结果以及图9显示了快速训练和更具表现力设计之间的权衡。

表格5：Titans的消融研究。Titans的所有组件都对其性能产生积极的贡献。

6 结论

在本文中，我们提出了一种神经长时记忆，作为元上下文学习器，在测试时学习记忆。神经记忆模块在本质上是一种循环模型，它可以自适应地记忆那些更令人惊讶或接近令人惊讶的标记。与现代循环模型相比，它具有更具表现力的记忆更新和存储机制。利用这个记忆，我们提出了Titans架构及其三个变体，其中我们建议将记忆模块作为（1）上下文、（2）门控和（3）层进行结合。我们在各种任务上的实验评估验证了Titans相对于Transformer和最近的现代线性循环模型更加有效，特别是对于长上下文。也就是说，Titans可以在大于2M上下文窗口大小时比基线模型具有更好的准确性。Titans已在Pytorch和JAX中实现，我们打算尽快提供我们用来训练和评估模型的代码。

参考文献 

省略。。。。。。

A相关工作

有多种独立的观点可以导致Titan或其组件的设计。因此，为了将我们的工作进一步放置在更广泛的背景下，我们回顾了三类研究。

A.1线性递归模型

最近，为了解决Transformer在训练和推断中的计算成本，线性循环模型引起了很多关注（Tiezzi等人，2024年），主要是因为其快速的推断和训练能力。第一代模型，比如RetNet（孙雨涛等，2023年）、LRU（Orvieto等，2023年）、RWKV（Peng，Alcaide等，2023年）、S5（J. T. Smith，Warrington和Linderman，2023年）和S4（顾，戈尔和瑞，2022年），使用了数据无关的转移矩阵/衰减机制。第二代此类模型开始将门控机制纳入其中，这是传统RNN中广泛使用的技术（Gers，Jürgen Schmidhuber和Cummins，2000年；Greff等，2016年；Van Der Westhuizen和Lasenby，2018年），并将这种线性体系结构融入其中，比如Griffin（De等，2024年）、SSMs（Behrouz，Santacatterina和Zabih，2024年；刀和顾，2024年；顾和刀，2024年；Hasani等，2023年）、RWKV6（彭，Goldstein等，2024年）。第三代线性循环模型基于更复杂的内存更新规则，基于元学习、在线学习和/或增量规则，产生了更具表现力和有效性的模型，如：Longhorn（刘彬等，2024年）、门控DeltaNet（S.杨，Kautz和Hatamizadeh，2024年）、TTT（孙宇等，2024年）和DeltaNet（S.杨，B.王，张宇等，2024年）。我们的LMM模型可以被视为这些模型的下一代，其中我们将标记流量纳入内存更新机制，具有更强大的内存更新过程。请参阅附录C，详细讨论不同的循环模型和Titans。

A.2基于Transformer的架构

Transformer. Transformers（Vaswani et al. 2017）作为许多深度学习模型的事实标准，基于注意力机制（Bahdanau 2014）。然而，它们遭受二次计算成本的困扰，限制了它们扩展到长上下文窗口的能力。为了改进较长序列的softmax注意力的内存消耗和吞吐量，各种研究集中在对注意力执行I/O感知实现（Dao 2024; Dao, D. Fu, et al. 2022），通过稀疏化注意力矩阵设计更高效的注意力机制（B. Chen et al. 2021；Choromanski et al. 2021；Dai et al. 2019；J. Dong et al. 2024；Roy et al. 2021），近似softmax（Arora et al. 2024），或开发基于内核（线性）的注意力（Aksenov et al. 2024；Kacham, Mirrokni, and P. Zhong 2024；Schlag, Irie, and Jürgen Schmidhuber 2021；S. Yang, B. Wang, Shen, et al. 2024）。

基于分段的Transformer。改善Transformer效率的另一种研究方向是基于分段或块的Transformer（Dai等人，2019）。分段Transformer的主要缺点是各个段之间完全隔离，因此上下文窗口仅限于分段的长度。为解决此问题，各种研究讨论了记忆的重要性，这可以帮助模型在分段之间传递信息（Bulatov、Yuri Kuratov等人，2023；Bulatov、Yury Kuratov和Burtsev，2022；Feng等人，2022；Hutchins等人，2022；Rodkin等人，2024；Z. Wang等人，2019；Q. Wu等人，2020；Zancato等人，2024）。Titans与这些模型的关键区别在于：（1）此类模型中的记忆是简单的小尺寸向量，缺乏压缩复杂信息的表达能力；（2）记忆模块缺乏遗忘机制，导致快速溢出；（3）只关注瞬时惊讶，缺少信息流。更具体地说，回顾循环记忆Transformer（RMT）（Bulatov、Yuri Kuratov等人，2023；Bulatov、Yury Kuratov和Burtsev，2022；Rodkin等人，2024），可以将Titans（MAC）视为RMT的泛化，其中我们使用了一个神经记忆模块而非向量值小尺寸记忆。

关于大型语言模型的记忆。另一个有趣的研究方向是在后训练将外部记忆模块与LLMs结合在一起（Z. He等，2024年; Khandelwal等，2020年; Y. Wang, Y. Gao等，2024年）。这些模型与我们的方法不同，因为我们将记忆作为初始架构的一部分并进行端到端的训练。此外，大部分这些显式记忆模块都面临着与基于块的Transformer相同的限制（如上所述）。关于这些模型的详细讨论，我们参考了Y. Wang，Han等人近期的研究（2024年）。

A.3测试时间训练和快速权重程序

记忆设计和内存增强。在文献中，大量的研究工作是设计能够通过递归记忆知识抽象（例如持久记忆）（Sukhbaatar、Grave等人，2019年）或记忆数据依赖性信息（也称为上下文记忆）的内存模块（Bulatov、Yury Kuratov和Burtsev 2022年;Rodkin等人，2024年;Zancato等人，2024年）、变形金刚（Berges等人，2024年;Cetin等人，2024年;Feng等人，2022年;Le、Tran和Venkatesh 2020;Munkhdalai、Faruqui和Gopal 2024;J. Zhang等人，2024年）、梯度（Irie、Csordás和Jürgen Schmidhuber 2022年;Munkhdalai，Sordoni，et al. 2019）或其他学习范式（Sukhbaatar，Weston，Fergus，et al. 2015;Weston、Chopra和Bordes 2014年）。然而，这些内存模型要么 （1） 基于瞬时惊喜，缺少数据流和事件，（2） 缺乏删除内存的遗忘机制，导致快速内存溢出 （3） 是固定大小的浅层（矩阵值）内存，导致在长上下文中性能不佳，以及 （4） 基于测试时的固定参数，缺乏测试时间适应性。 

各种研究已广泛探讨了这些模型（Irie, Schlag等，2021年；Munkhdalai, Sordoni等，2019年；Munkhdalai和H. Yu，2017年；Schlag、Irie和Jürgen Schmidhuber，2021年；JH Schmidhuber，1992年；S. Yang，Kautz和Hatamizadeh，2024年；S. Yang，B. Wang，Yu Zhang等，2024年）。然而，所有这些模型都基于瞬时惊喜，缺乏序列中的标记流动（请参见第3.1节），大多数缺乏遗忘门，导致记忆管理不佳。

测试时间训练。学习测试时间或学习以学习的关键思想（即（Andrychowicz等，2016））可以追溯到很早以前对本地学习Bottou和Vapnik 1992的研究，在这种方法中，在进行预测之前，对每个测试数据样本进行训练其邻居（Gandelsman等，2022; H. Zhang等，2006）。这种方法在视觉任务中已经显示出有希望的性能（Jain和Learned-Miller 2011; Mullapudi等，2019），这主要是由于它们减轻了分布外样本的能力。在这个方向上，与我们最相似的研究是MNM（Munkhdalai，Sordoni等，2019）和TTT层（Yu Sun等，2024），我们在附录C中讨论了它们的关键差异。

B语言模型和常识推理数据集

最近对线性递归模型进行了研究（Dao和Gu 2024; S. Yang, Kautz和Hatamizadeh 2024; S. Yang, B. Wang, Yu Zhang等人2024），我们使用了Wikitext（Merity等人2017）、LMB（Paperno等人2016）、PIQA（Bisk等人2020）、HellaSwag（Zellers等人2019）、WinoGrande（Sakaguchi等人2021）、ARC-easy（ARC-e）和ARC-challenge（ARC-c）（P. Clark等人2018）、SIQA（Sap等人2019）和BoolQ（C. Clark等人2019）。此外，400M模型的基准结果来自S. Yang, Kautz和Hatamizadeh（2024）的报告结果。

C长期记忆模块 （LMM） 作为序列模型

在本节中，我们讨论作为序列模型的LMM如何与现代线性循环模型相连接。为了简单起见，我们从线性记忆开始，其中M𝑡 = 𝑊𝑡 ∈ R𝑑in×𝑑in。在这种情况下，我们的目标函数变为ℓ(M;𝑥𝑡) = 12 ∥M𝑡k𝑡 − v𝑡 ∥22，其中我们使用动量梯度下降和权重衰减进行优化。因此，重新审视等式13中的循环公式：

LMM是Generalized Gated DeltaNet。根据S. Yang、Kautz和Hatamizadeh（2024）的讨论，DeltaNet（S. Yang, B. Wang）是Generalized Gated DeltaNet。

张宇等（2024）可以被解释为优化L = 12 ∥S𝑡k𝑡 − v𝑡 ∥22的在线学习问题，从而产生：

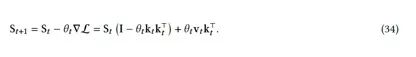在这个公式中，门控DeltaNet与上述相同，但额外增加了一个权重衰减项（S. Yang，Kautz和Hatamizadeh 2024）。比较方程式32和方程式34，我们可以看到设置𝜂𝑡 = 0导致两个公式等价。因此，我们可以说，LMM从三个方面概括了最近对门控DeltaNet的研究（S. Yang，Kautz和Hatamizadeh 2024）。

1.基于动量的规则：Delta规则基于即时的惊讶度，这意味着Token的流动不能影响内存更新规则。然而，LMM基于一个动量规则，同时考虑过去和即时的惊讶度。

2.深层记忆：虽然门控DeltaNet受限于线性（矩阵值）存储器，因为需要找到闭合递归形式，LMM通过使用基于梯度的表达式，实现了使用深层存储模块，从而提高了表达能力。

3.非线性递归：DeltaNet和Gated DeltaNet基于线性递归，而我们的LMM采用了区块间非线性递归和区块内线性递归。这种设计使得LMM具有更高的表达能力。

在这里，我们讨论了门控DeltaNet作为最新一代循环模型的示例。类似的方法，如RWKV-7（Peng 2021），也使用相同的公式和损失函数，因此LMM将所有这样的模型泛化。

LMM是广义的长角。类似于DeltaNet，Longhorn（B. Liu等，2024年）使用相同的损失函数，但是它使用隐式在线学习导出闭合形式：

 𝛿𝑡 = 1+𝜃𝜃𝑡k𝑡𝑡k𝑡⊤是LMM的一部分。然而，它缺乏一个遗忘门，导致内存溢出更快。因此，除了(1)基于动量的规则、(2)深度记忆和(3)非线性循环的特点之外，LMM还具有使用额外的(4)遗忘门的优势，从而实现更好的内存管理。

LMM是广义TTT层。据我们所知，TTT（Yu Sun等人，2024年）是唯一采用基于梯度更新规则的现代线性递归模型。除了不同的架构设计和目标函数外，我们的LMM与提出的TTT层（Yu Sun等人，2024年）有三个关键的区别：

1.遗忘机制：TTT层在每个时间步更新内存，没有机会忘记过去的数据。因此，当固定内存大小时，模型不能管理长序列的记忆。类似于LMM的遗忘机制允许在不再需要过去信息时清除内存。我们证明，在一般情况下，这种遗忘机制等效于权重衰减，并提供了一种将其快速融入并行训练的方法。

2.基于动量的更新规则：TTT层基于瞬时的惊奇，意味着Token的流动不能影响记忆更新规则。然而，LMM基于动量规则，考虑了过去和瞬时的惊讶。有关此设计的动机，请参见第3.1节。

3. 深度记忆：TTT层允许更深的记忆，但是这种更深的记忆模块的优缺点尚未进行实验评估。

据我们所知，我们的神经长期记忆模块是第一个具有基于动量的线性循环模型的模块。

最后，与上文以及其他最新的线性循环研究有一个关键区别在于，请注意现代线性模型的混合变体——如Griffin（De等人2024）、DeltaNet（杨，王，张等人2024）、Gated DeltaNet（杨，Kautz和Hatamizadeh 2024）、H3（傅等人2023）、Mamba2（刀和顾2024）、Samba（任等人2024）等——都基于逐层设计。我们提出Titans来展示如何有效地将这些记忆模块纳入体系结构中。