树状数组趣解

树状数组

感谢各位能在白忙之中抽空来看鄙人的文章，cgg在这有礼了！

1、初识树状数组

先给张图。

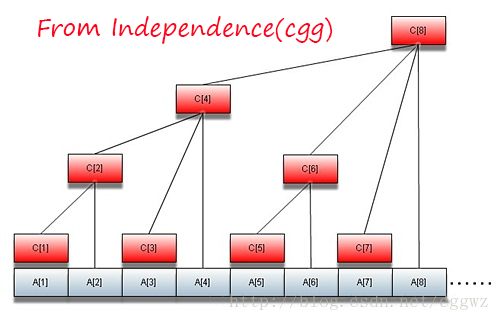
下面的A[]是原数组，而C[]则是A[]对应的树状数组。所以你应该会恍然大悟（也许夸张了些），树状数组是数组的另一种表现形式，而这种表现形式会大大提高其各种操作的效率，在竞赛中，也时常会考察，那么下面，就让我们一起去解开他神秘的面纱吧！

2、对应关系

有的人看到后会有点发懵，A[]和C[]的对应关系是怎样的呢？我们先写前几项看一下。

• C[1]=A[1]
• C[2]=A[1]+A[2]=C[1]+A[2]
• C[3]=A[3]
• C[4]=C[2]+C[3]+A[4]=A[1]+A[2]+A[3]+A[4]
• C[5]=A[5]
• C[6]=C[5]+A[6]=A[5]+A[6]
• C[7]=A[7]

• C[8]=C[4]+C[6]+C[7]+A[8]=A[1]+A[2]+…+A[8]
  有什么发现？依然没头绪？
  没头绪也没事，让我来告诉你吧！
  C[i]=A[i-2^k+1]+A[i-2^k+2]+…+A[i]
  你可能会奇怪，k是什么？
  这别急，让我们先来找找规律。
  下面让我们换一种方式写，我们用二进制来写。

• C[0001]=A[0001] {k=0}

• C[0010]=C[0001]+A[0010] {k=1}
• C[0011]=A[0011] {k=0}
• C[0100]=C[0010]+C[0011]+A[0100] {k=2}
• C[0101]=A[0101] {k=0}
• C[0110]=C[0101]+A[0110] {k=1}
• C[0111]=A[0111] {k=0}

• C[1000]=C[0100]+C[0110]+C[0111]+A[1000] {k=3}
  这回又有什么发现？这回你应该有些发现了。
  如果你说，k是右边式子的C[]出现的次数。
  额，这没错，但不是我想要说的。
  为什么要用二进制？
  如果你说，k为左边C的坐标末尾的0的个数，那么恭喜你，答对了，这正是我想告诉你们的。
  那么，我们怎么在程序中获取2^k？
  在说这个之前，我们还得提一个规律，我们会发现，等号左边的下标有k个0，那么右边的几个C的下标末尾分别有（k-1）、（k-2）……1、0个0，并且这些下标均小于左边的下标。
  这有什么用？这先不急，我们后面就会看到它的用初了。
  下面先讲怎么求2^k。

  3、获取对应区间

  原理

  原理简单，就是我们讲的末尾0的个数，那么我们怎么获取呢？
  刚刚用了二进制，所以可能自然而然地想到了位运算。
  没错，我们正是要用位运算来解决这个问题。这里先给出计算公式。

2^k=i&(i^(i-1))
2^k=i&(-i)

这里给出了两个公式，都能计算出来2^k，这样我们也就能进行必要的操作了。
那么为什么是这两个公式呢？下面我们就说一下原理。
先举例，如10100
1、运用公式一
i-1=10011
x=i^(i-1)=00111
i&x=00100=4=2^2
k=2
没有任何问题，那么为什么呢？
首先，减一，会导致末尾的0全部变成1，且原来最后一个1变成0，自己想想竖式计算，0减1的时候需要向高位借一位。
接下来异或，原数最后一个1左边位没变化，所以异或肯定是0，而原数最后一个1，减1后变成0，所以该位异或后肯定为1，而原数末尾的0，减1后变成1，所以以后结果也为1，综合一下，就是自最后一个1以后全为1，而其他位为0.
最后一步，按位与，x中0的为肯定都为0，而1的位，只有原数i最后一个1为1，其他结果均为0，又因为，这个1是从左往右数第（k+1）位，所以是2^k。
应该听懂了吧！
2、公式二
这里简单解释一下，首先你得弄清补码是啥，因为负数的二进制就是通过补码实现的。一个负数的二进制就是它绝对值的二进制表示取反再加一。那么我们看看-i的二进制应该是怎样的，首先取反，原来最后一个1变成0，而末尾0变成1，其他位也取反，接下来在加1，会怎样？末尾1又变成0，而i中最后一个1变成0后又因为进位变成1，前面为仅仅为原数相反不变。总结一下就是，最后一个1及其右边的数不变，而其他位取反。
那么接下来按位与，由于取反的其他位与原来位相反，结果肯定为0，而末尾0，结果肯定为0，只有最后一个1，一直没变，所以结果依然为1，这就回到了公式一中最后的结果。

代码

有了公式，代码就很简单了，这里给出方便大家学习。
公式一

int lowbit(int x){
    return x&(x^(x-1));
}

公式二

int lowbit(int x){
    return x&(-x);
}

4、操作

操作主要有3种：插入操作，求前k个数之和，求区间[l,r]的和。

代码

插入操作

void insert(int x,int p){//将坐标x的数加上p
    while(x<=n){
        C[x]+=p;
        x+=lowbit(x);
    }
}

求前k个数之和

int sum(int k){
    int ans=0;
    while(k>0){
        ans+=C[k];
        k-=lowbit(k);
    }
    return ans;
}

求区间[l,r]的和

int ask(int l,int r){
    return sum(r)-sum(l-1);
}

这里我们有几个约定：C[]是树状数组，n是C[]的大小。

原理

插入操作

插入操作只是我们给的代码的一种特殊情况，即原数等于0的时候。
我们所要做的，不仅是将原数组的对应值改掉，我们还要将树状数组中包含这个值的结点的值改变。
值得解释的，也就是下面这句话：

x+=lowbit(x);

还记得我前面卖的关子吗？左右下标的关系。这里就用到了。
lowbit（x）的结果就是一个除了x二进制最后一个1的位置是1，其他均为0，所以x+lowbit(x)结果就是末尾多了0，这也就符合我们前面的那个规律了。

求前k个数之和

这个就更好解释了，因为每个数负责的是A[i-2^k+1]到A[i]的和，所以加上C[x]后，很自然的让x-2^k(即x-lowbit(x))，得到C[i-2^k]，而这正是C[x]负责的范围的左边。

求区间[l,r]的和

这个我觉得可以不用讲了，
sum(l-1)=A[1]+……+A[l-1]
sum(r)=A[1]+……+A[r]
所以下式减上式就得到
A[l]+A[l+1]+……+A[r]

5小结

树状数组在信息学竞赛中会用到，希望大家能透彻理解这篇文章，还要多做做题，以巩固所学的知识。
如有讲的不对的地方，希望各位能和鄙人多多交流。多谢各位捧场。