FinFET全加器在32纳米的鲁棒性研究

多栅器件与求和电路协同设计在32纳米技术节点的鲁棒性研究

1 引言

执行算术运算的模块在大多数电子系统中都很常见。数字加法是一种基本的算术运算，也是各种其他常用数学运算的基础。因此，1位全加器单元是数字系统中算术逻辑单元（ALU）不可或缺的基本构建模块。为了提高数学运算模块的高速和低功耗性能，提升全加器单元的性能至关重要（Rabaey等人 2002；Zimmermann和Fichtner 1997）。在超大规模集成电路（VLSI）中，针对低功耗和高性能的数字电路设计，迫切需要研究多栅器件的性能，以增强数字系统的可靠性。当前，电池供电设备的需求日益增长，对高运行速度和低功耗提出了更高要求（Shams等人 2002）。

过去几年的研究证明，在最小能耗点（MEP）下运行器件会导致传播延迟（tp）显著增加。然而，最小能耗延迟点在延迟和能耗方面提供了更高的电路性能，已成为研究人员关注的焦点。电子电路还有另一类应用，这类应用要求极低能耗并具备中等性能。此类电路必须在最小能耗点下运行，以实现极低的能耗水平。这标志着设计思路的重大转变：设计起点不再是追求最大性能，而是以最小能耗点为首要目标。文献表明，最小能耗点出现在亚阈值区（Enz等人 1995；Vittoz 2005；Calhoun等人 2005）。其应用范围有限，因此迫切需要通过采用新器件/新技术或确定合适的工作点来解决性能与能耗之间的权衡问题。

本文提出了一种基于FinFET的静态1位全加器单元，该设计在保持接近最小能耗点的同时，有助于弥补性能上的巨大损失。与MOSFET对应的全加器相比，提出的设计在功耗增加1.36×的情况下，实现了更高的计算速度（提升7.96×）、更低的能量消耗（降低5.86×）以及更低的能耗延迟积（EDP）（降低21.08×）。此外，该设计在面对工艺变化时表现出更强的鲁棒性，其功耗分布在（改善3.20×）、延迟分布（改善4.70×）、PDP（功耗延迟积）分布（改善3.35×）和EDP分布（改善3.14×）方面均比MOSFET对应设计更加集中。这些改进得益于在全加器设计中采用了新的FinFET技术。该技术中的多栅器件受随机掺杂波动（RDF）以及阈值电压滚降、漏致势垒降低（DIBL）等短沟道效应的影响较小。为了证明本设计的优越性，本文还分析了另外五种1位全加器单元，并从功耗、延迟和PDP等方面与提出的设计进行了比较。我们使用32纳米预测技术模型（PTM）参数在SPICE平台上进行仿真。

这是器件在能量和速度均处于可接受范围内的工作点。我们提出的设计策略是在中等反型区（MIR）设计1位全加器，以实现能效高且性能适中的目标（Markovic等人，2010；Dokania和Islam 2015）。为此，我们将器件工作在其阈值电压附近或等于阈值电压下。

本文提出了一种采用FinFET（Shang 2006）的静态1位全加器单元（数字加法电路）。该设计有助于在电路工作于亚阈值区时恢复因性能下降带来的巨大损耗，同时仍保持接近最小能耗点。我们还通过改变工艺/器件参数和电压对电路进行了变异分析。通过在100 MHz频率下运行电路，进行了分析与比较。我们使用32纳米预测技术模型参数（PTM 2008），在SPICE上进行了大量仿真以验证设计。

本文其余部分组织如下。第2节简要讨论技术缩放对器件特性的影响。第3节简要回顾1位全加器单元。第4节分析了各种基于MOSFET的求和电路，并将结果与提出的基于FinFET的设计进行比较。第5节讨论工艺和电压变化对基于FinFET的全加器的影响。第6节对本文进行总结。

2 技术微缩对器件特性的影响

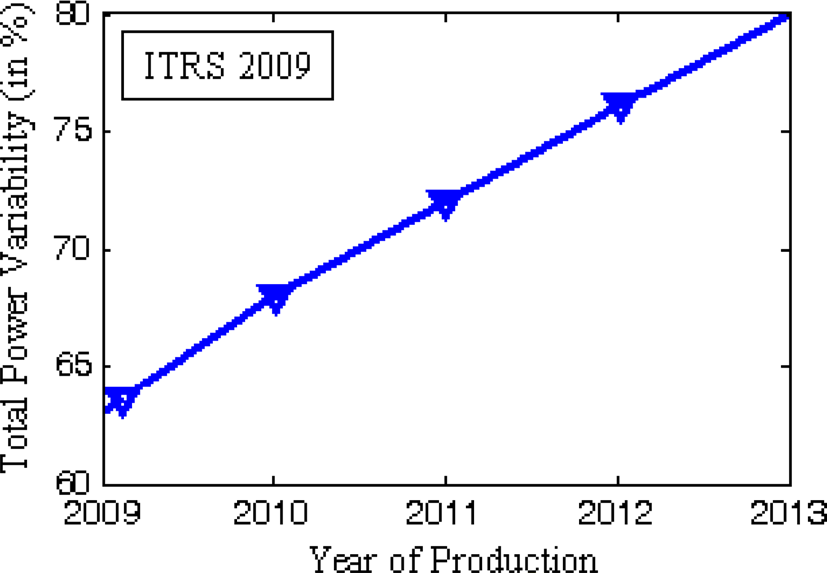
我们正处于纳米尺度时代，为了继续推进摩尔定律，需要克服各种挑战。激进的技术微缩对器件特性有诸多负面影响。存在多种可变性来源，例如光学邻近校正（OPC）、相移掩模（PSM）、布局引起的应变以及阱邻近效应。另一种影响器件几何参数（L（栅极长度）、W（栅宽）、tox（栅氧化层厚度）、LER（线边粗糙度）、LWR（线宽粗糙度））和阈值电压Vt的关键工艺变异源是随机掺杂波动（RDF）（Asenov等，2002；Asenov等，2003；Kuhn，2008；Bernstein等，2006；Saha，2010；Seoane等，2014）。各种短沟道效应（SCEs），如漏致势垒降低（DIBL），会引起阈值电压Vt的滚降。参数如L、W、tOX、NA等的变化，进而导致性能、漏电功耗、总功耗等各种设计指标出现显著变化。例如，在2013年生产年份，性能变化可能超过63%（图1）。此外，预计到2013年，总功耗和漏电功耗的变化将分别超过80%和287%（图2、图3）（ITRS 2009）。

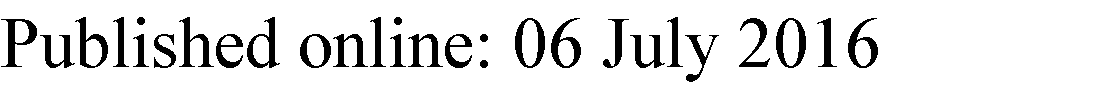
3 1位数字加法电路

1位加法器电路是算术逻辑单元（ALU）的组成部分，而算术逻辑单元是微处理器（μP）/数字信号处理器（DSP）中的关键模块。静态CMOS全加器通过实现CO（进位输出）项来实现，该进位输出项在S（和）项中被复用为一个公共子表达式。在本研究中，实现了用于S（和）和CO（进位输出）的以下布尔方程。

其中CO是CO的补码。我们可以从1位全加器的真值表（见表1）推导出这些布尔方程。

从真值表1，CO和 S 可以表示为

$$ CO = AB + C(A + B) $$
$$ CO = AB + BC + CA = AB + C(B + A) $$
$$ S = ABC + ABC + ABC + ABC $$

$$ CO = AB + BC + CA = AB \cdot BC \cdot CA $$
$$ CO = (A + B) \cdot (B + C) \cdot (C + A) $$
$$ CO = (AB^c + AC^c + B^c + BC) \cdot (C^c + A) $$
$$ CO = ABC^c + AC^c + BC^c + BC^c + AB^c + AC^c + AB^c + ABC $$
$$ CO = ABC + A C + BC + AB $$
$$ \therefore (A + B + C) \cdot CO = (A + B + C) \cdot (ABC + A C + BC + AB) = (0+0+ ABC+0)+(0+ ABC+0+0)+(0+0+0+ ABC) $$
$$ (A + B + C) \cdot CO = ABC + ABC + ABC $$
$$ \therefore S = ABC + ABC + ABC + ABC = RHS\ of\ S (known\ from\ TT) $$

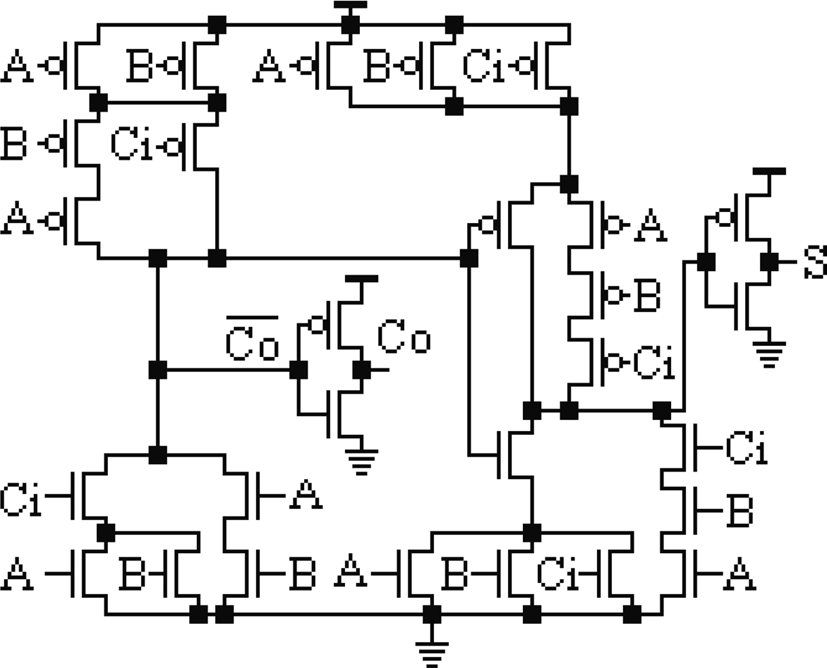
使用互补CMOS逻辑风格实现布尔函数的第一步是推导下拉网络（PDN）。下一步是使用对偶性以分层方式推导上拉网络（PUN）。互补型MOSFET或FinFET实现（1）和（2）是直接的。下拉网络（PDN）由n型场效应晶体管实现，上拉网络（PUN）由p型场效应晶体管实现。在PDN中，与（或）功能通过串联（并联）连接的nFET实现。为了实现PUN，PDN中的串联（并联）nFET需改为并联（串联）连接。以此方式实现可得到反相输出。为获得原相输出，需使用反相器。如图4所示的1位全加器实现中，CO和S在经过反相器后以原相形式获得。

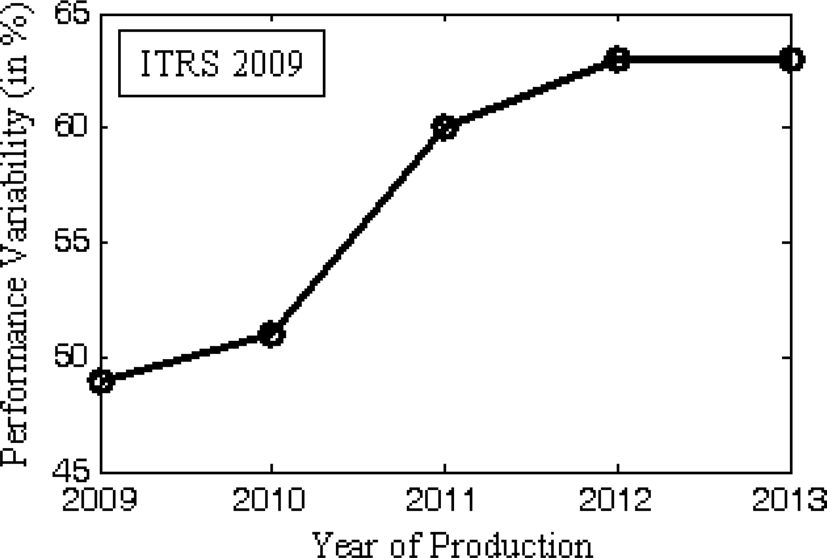
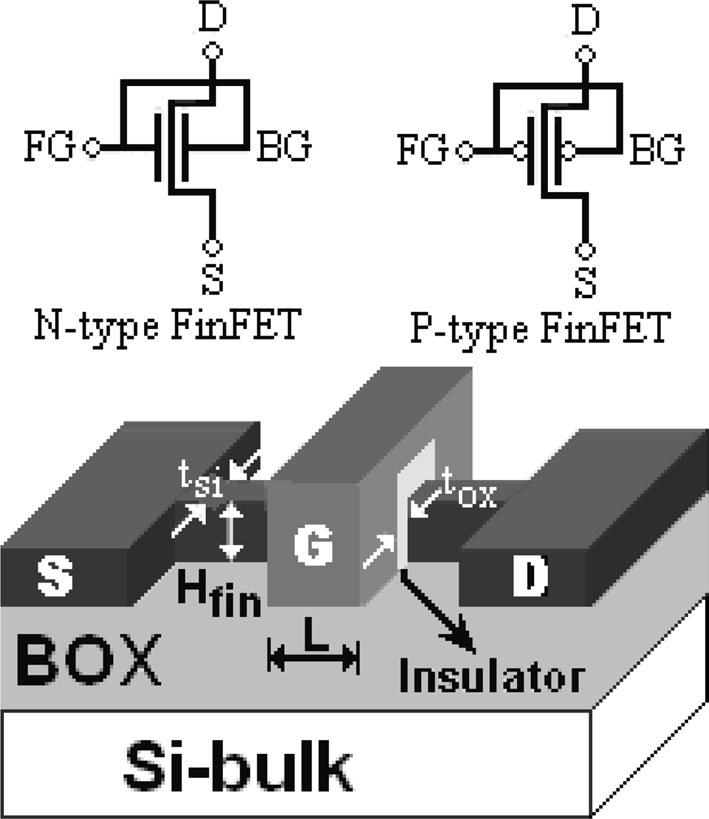
图5 显示了N型FinFET、P型FinFET和FinFET结构。FinFET分为P型或N型，也称为非平面双栅极金属氧化物半导体场效应晶体管（DG-MOSFET），其中前栅极（FG）和背栅极（BG）连接在一起。除了两个连接的栅极端子外，它仅有漏极和源极端子，而没有衬底端子。FinFET结构中的双栅极相比单栅极金属氧化物半导体场效应晶体管提供了更优的电学特性。根据以往研究观察，有前景的多栅极晶体管展现出显著优势（Kim 2005; Tawfik和Kursun 2008; Vaddi等人 2010）。它在保持亚阈值漏电流ID（漏源之间）和栅极漏电流ISUB低于可容忍范围的同时，提高了IG，相较于传统的单栅极MOSFET（SG-MOSFET）。FinFET的多个栅极在电气上相互连接，其tsi（薄硅体）能够有效抑制短沟道效应（SCEs），并降低ISUB和IG，从而减少总漏电功耗。以往的研究还发现，多栅极器件比传统单栅极器件具有更好的参数变化免疫性。对称栅极双栅极FinFET的架构如（Tawfik和Kursun 2009）所示。鳍片厚度和栅氧化层厚度是鳍式场效应晶体管设计中最关键的尺寸。这些参数对FinFET架构抑制短沟道效应和参数变化敏感性的效率具有重要影响（Tawfik和Kursun 2009）。

4 全加器单元的分析与比较

本节分析了各种基于MOSFET的全加器单元，并将结果与所提出的基于FinFET的设计进行了比较。

4.1 基于鳍式场效应晶体管的提出的设计及其金属氧化物半导体场效应晶体管对应结构的分析

由于随机掺杂波动（RDF）引起的片内阈值电压（Vt）变化，导致全加器单元的设计指标发生变化。由于RDF引起的单元晶体管的Vt偏移被视为具有σVt（Vt的标准差）的独立高斯随机变量，其表达式如下（Taur和Ning 2009；Mukhopadhyay等 2005）

$$ \sigma_{vt} = \frac{q t_{ox}}{\varepsilon_{ox} N_A W_{dm} \sqrt{3LW}} $$

其中q为电子电荷，tox为氧化层厚度，εox为氧化物介电常数，NA为衬底掺杂浓度，L为栅极长度，W为器件的栅宽，Wdm为耗尽区的最大宽度。

$$ W_{dm} = \sqrt{\frac{4\varepsilon_{si} kT \ln(N_A/n_i)}{q^2 N_A}} $$

其中，k 是玻尔兹曼常数，ni 是本征载流子浓度，εsi 是硅的介电常数。由公式 (4) 可明显看出，Wdm 随温度变化而变化。由公式 (3) 和 (4) 可知，σVt（Vt 的标准差）依赖于工艺参数，如 tox（氧化层厚度）、NA（衬底掺杂浓度）、器件参数如 L（栅极长度）和 W（栅极宽度），以及温度。它还依赖于电源电压（VDD）（因为 VGS = VDS = VDD），由于栅氧化层电容（COX = εOX/tox）在一定程度上也与电压相关。此外，由于漏致势垒降低（DIBL），Vt 还依赖于 VDS。在短沟道器件中，Vt 的微小变化可表示为

$$ \Delta V_t = \frac{24 t_{OX}}{W_{dm}} \left[ \sqrt{V_{bi}(V_{bi} + V_{DS})} - a(2\Phi_F) \right] e^{-\pi L / 2 W_{dm}} + 3t_{OX} $$

其中 a = 0.4，2ΦF = ΦS 为表面势，Vbi 为内建电势。

由(5)式可知，当VDS(L)取值较高（较低）时，∆Vt将取较高值，导致Vt滚降（减小）更显著。

由于在纳米级金属氧化物半导体场效应晶体管中，栅极长度、宽度、氧化层厚度和衬底掺杂浓度的变化不可避免，且由于工艺、电压和温度变化导致的Vt变化（Vt的标准差）是不可避免的，我们已进行蒙特卡洛分析以估算设计指标。设计指标（延迟、功耗、功耗延迟积等）的均值相对于标准差的值越低，表明设计的鲁棒性越强。

通过在 VDD 超过 Vt 的情况下分析一位数字加法电路，输入频率为100 MHz。仿真采用50飞法的负载电容、50摄氏度的温度，并使用最小尺寸晶体管。本设计中采用的N型FinFET和P型FinFET如图5所示。本设计通过将传统基于MOSFET的全加器（图4）中的所有N型MOSFET和P型MOSFET替换为其FinFET对应器件来实现。

平均功耗（Pavg）使用以下方程估算，并在图6中绘制。

$$ P_{avg} = \frac{1}{T} \int_0^T p(t) dt = \frac{V_{DD}}{T} \int_0^T i_{VDD}(t) dt $$

传播延迟（tp）通过以下方程计算，并在图7中绘制。对于使进位输出 CO 发生转换的输入进位信号 Ci（以及其他输入A和B），我们得到

$$ C_L \frac{dV_{CO}}{dt} = I_{PUN}(Ci, CO) - I_{PDN}(Ci, CO) $$

传播延迟（tp）通过取低到高传播延迟（tpLH）和高到低传播延迟（tpHL）的平均值来估算，如以下所示

$$ t_p = \frac{t_{pLH} + t_{pHL}}{2} $$

其中 tpLH 和 tpHL 是阈值电压 (Vt)、负载电容 (CL)、电源电压 (VDD) 以及增益因子 (β= με0 εr/tox(W/L)) 的函数。tpHL 从导致 CO 转换的输入进位信号 (Ci) 达到其 50%点时开始计算，到输出进位信号 (Co) 从其初始高电平达到其 50%点时结束。tpLH 从导致 CO 转换的输入进位信号 (Ci) 达到其 50%点时开始计算，到输出进位信号 (Co) 从其初始低电平达到其 50%点时结束。这是因为 tpLH 和 tpHL 是 Ci = VDD/2 与 CO = VDD/2 之间的延迟时间。当 Ci = VDD/2 时，CO 即将从其稳态值开始切换。在下拉延迟 (tpHL) 或上拉延迟 (tpLH) 期间，CO 的变化量为 ≈VDD/2。由于在 CO 的下拉转换过程中，IPUN 可忽略不计，因此可对 (7) 进行积分得到

$$ \int C_L dV_{CO} = \int (I_{PUN}(Ci, CO) - I_{PDN}(Ci, CO)) dt $$
$$ \int_{V_{DD}/2}^{V_{DD}} C_L dV_{CO} = \int_{V_{DD}/2}^{V_{DD}} -I_{PDN}(Ci, CO) dt $$
$$ t_{pHL} = -\int_{V_{DD}/2}^{V_{DD}} \frac{C_L dV_{CO}}{I_{PDN}} = \frac{C_L V_{DD}/2}{I_{PDN,avg}} $$

类似地，由于在 CO 的上拉转换过程中，IPDN 可忽略不计，因此可对 (7) 进行积分得到

$$ t_{pLH} = \int_{0}^{V_{DD}/2} \frac{C_L dV_{CO}}{I_{PUN}} = \frac{C_L V_{DD}/2}{I_{PUN,avg}} $$

由(9)和(10)可得，CO 的传播延迟(tp)可表示为

$$ t_p = \frac{C_L V_{DD}}{4} \left( \frac{1}{I_{PDN,avg}} + \frac{1}{I_{PUN,avg}} \right) $$

功耗延迟积（PDP）通过（12）计算，并在图8中绘制。

$$ PDP = P_{avg} \times t_p $$

我们通过改变电源电压，对基于MOSFET的全加器和基于FinFET的全加器进行了仿真，从0.47至1 V，步长为0.01 V。仿真结果列于表2中。基于仿真数据的平均功耗、传播延迟和功耗‐延迟积（PDP）也分别在图6、7和8中绘制，以便于直观比较。

多栅器件与求和电路协同设计在32纳米技术节点的鲁棒性研究（续）

4 全加器单元的分析与比较（续）

4.1 基于鳍式场效应晶体管的提出的设计及其金属氧化物半导体场效应晶体管对应结构的分析（续）

从表2和图6可以看出，在所有考虑的电源电压下，基于FinFET的全加器单元消耗的功耗更高，因为FinFET具有更高的驱动电流。

从表2和图7可以看出，在所有考虑的电源电压下，采用鳍式场效应晶体管的全加器单元比采用传统MOSFET的全加器单元具有更低的延迟，因为鳍式场效应晶体管具有更高的电流驱动能力。除了延迟更低之外，在降低电源电压时延迟的增加也十分有限。显然，基于传统MOSFET的全加器单元性能受到严重影响，因为随着电压缩放，延迟急剧增加。

尽管降低电源电压是降低功耗的最简单方法，因为有源功耗随VDD的平方成比例下降，但对于传统基于MOSFET的全加器电路而言，延迟增加仍然是限制电压缩放以降低功耗的重要障碍。通过使用鳍式场效应晶体管（FinFET）可以最小化在缩放电源电压下的性能损失。从表2和图8可以看出，基于FinFET的全加器单元在电压缩放下功耗延迟积极显著降低，同时延迟惩罚可忽略不计，仅以轻微增加功耗为代价。与提出的设计相比，传统基于MOSFET的全加器在电压缩放下PDP的降低并不明显。

功耗延迟积（PDP）是平均功耗（Pavg）与传播延迟（tp）的乘积，用于衡量翻转目标节点所需的能量，这无疑是一个重要指标。然而，对于给定电路，通过降低电源电压，该数值可以被任意降低。因此，电路运行的最佳VDD应为仍能确保电路正常工作的最低可能值。当然，这将以性能大幅下降为代价。如果能够有一种指标将性能度量结合起来，将会更好。

能量‐延迟积（EDP）正是用于衡量这一综合指标。EDP的计算公式为

$$ EDP = PDP \times t_p = P_{avg} \times t_p \times t_p $$

其中Pavg由(6)给出，tp由(8)给出，该值可近似为

$$ t_p \approx \frac{\alpha C_L V_{DD}}{V_{DD} - V_{Te}} $$

其中α为工艺参数，VTe = Vt + VDSAT/2，其中Vt为阈值电压，VDSAT为相对于源极的饱和漏极电压。假设电路的期望输出节点（S或CO）以最大可能切换频率fmax = 1/(2tp)工作，并忽略静态电流和短路电流对功耗的贡献，则得到

$$ PDP = C_L \times V_{DD}^2 \times f_{max} \times t_p = \frac{C_L \times V_{DD}^2}{2} $$

将tp和PDP的值分别从(14)和代入(13)，得到(15)

$$ EDP = \alpha C_L^2 \frac{V_{DD}^3}{2(V_{DD} - V_{Te})} $$

通过对(16)式关于VDD求导，并将结果等于0，得到最优的VDD如下：

$$ \frac{\partial(EDP)}{\partial V_{DD}} = 0 \Rightarrow 4\alpha C_L^2 V_{DD}^3 = 6\alpha C_L^2 V_{DD}^2 V_{Te} \Rightarrow 2V_{DD} = 3V_{Te} $$

因此，最优的VDD被获得为

$$ V_{DDopt} = \frac{3V_{Te}}{2} $$

本工作中所用金属氧化物半导体场效应晶体管的零偏置阈值电压为~500 mV。由于我们希望实现近阈值计算(NTC)的优势，因此对一个n型MOSFET在VDS = VGS = 500 mV条件下进行仿真，以估算VDSAT（饱和漏极电压）。估计得到的VDSAT为103 mV。因此，我们得到最优的VDD（VDDopt）= (500 + 103/2) mV = 551.5 mV。

在SPICE上进行了广泛的仿真，采用VDD = 0.55 V作为中等反型区（MIR）下的最佳VDD。所提出的设计采用了在（Tawfik和Kursun 2009）中优化的鳍式场效应晶体管结构的工艺参数。在VDD = 0.55 V下全加器单元的关键设计指标如表3所示。括号内为归一化值。

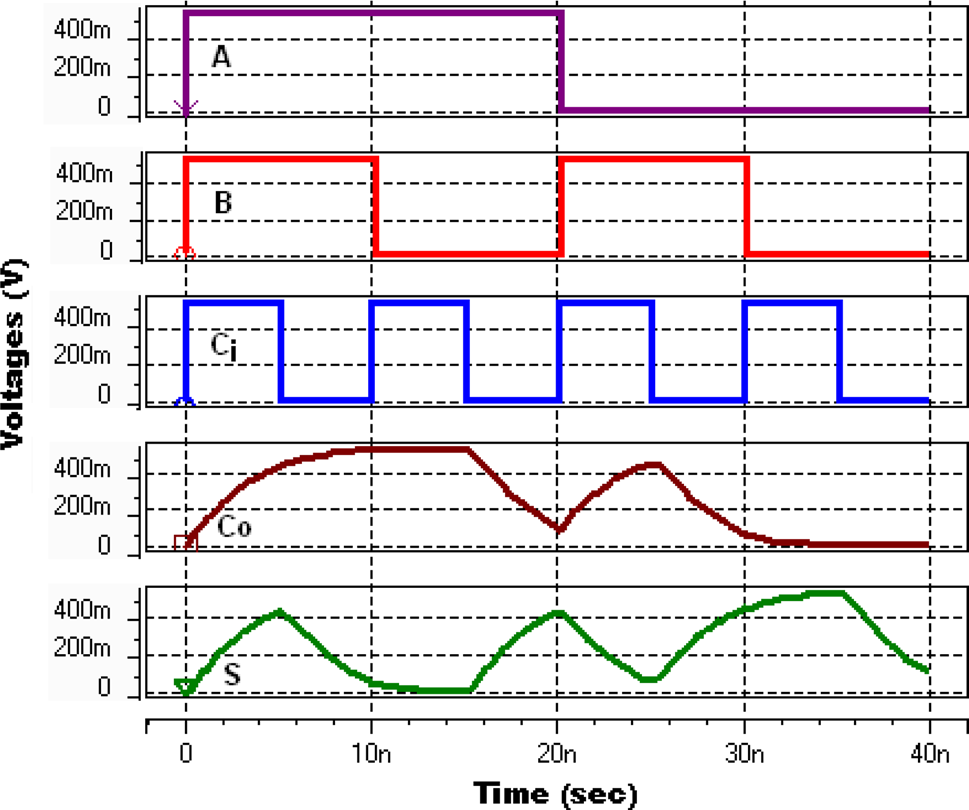
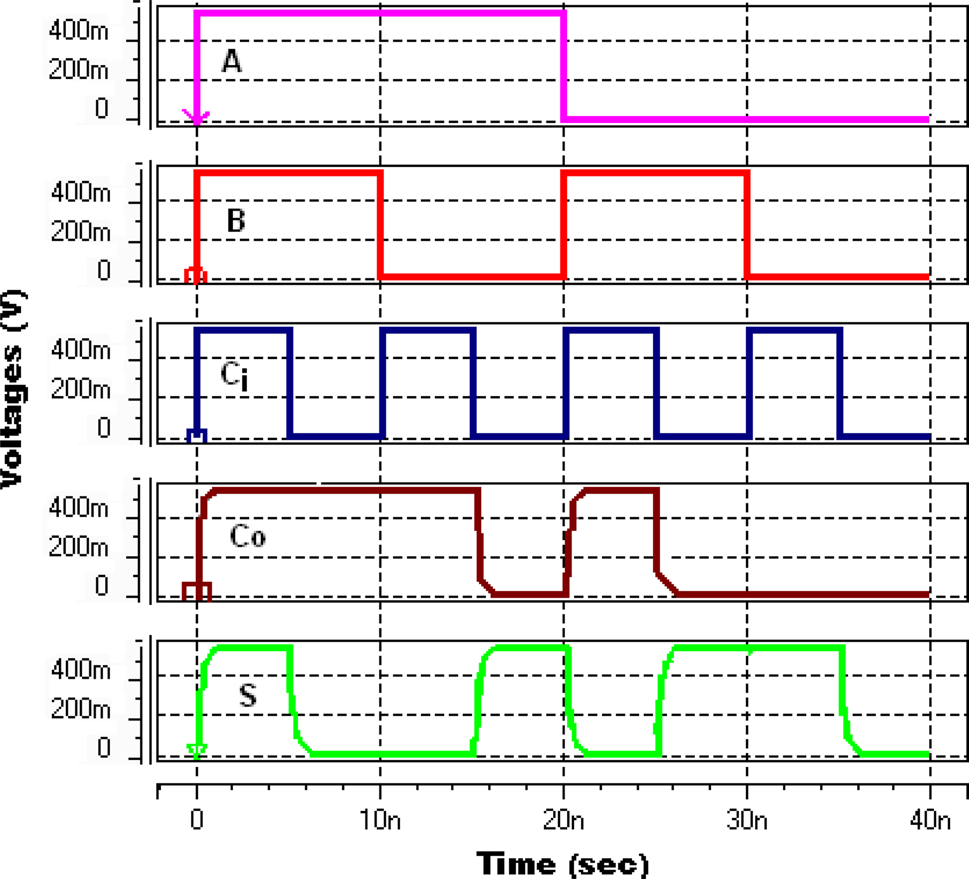
可以看出，在VDD = 0.55 V下采用鳍式场效应晶体管的数字加法电路延迟降低了7.96×，功耗延迟积降低了5.86×，但功耗增加了1.36×。在相同工作（最优）电压下，延迟减小而功耗增加。这是由于鳍式场效应晶体管具有更好的驱动能力（Vaddi等人 2010；Tawfik和Kursun 2009）。功耗延迟积的降低是因为延迟的减少幅度超过了功耗的增加幅度。在SPICE仿真过程中，对全加器在最优电源电压下的功能验证波形进行了捕获，如图9和图10所示。

4.2 五个额外的全加器单元分析，用于与标准CMOS全加器和基于鳍式场效应晶体管的提出的设计进行比较

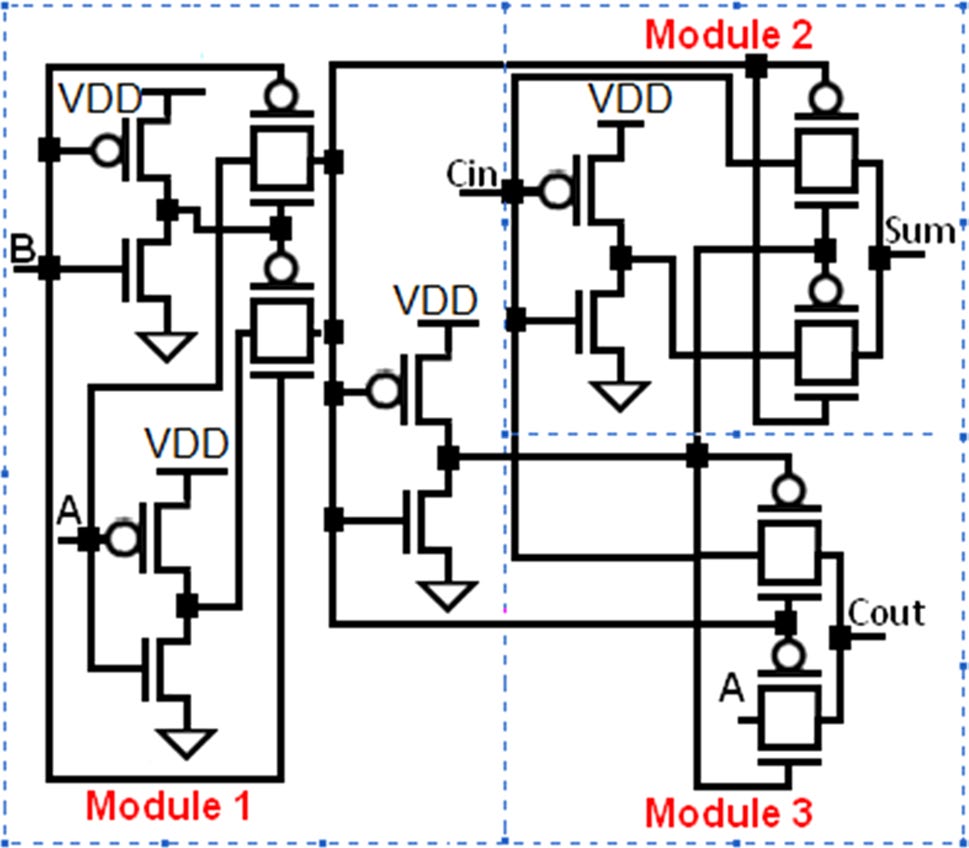
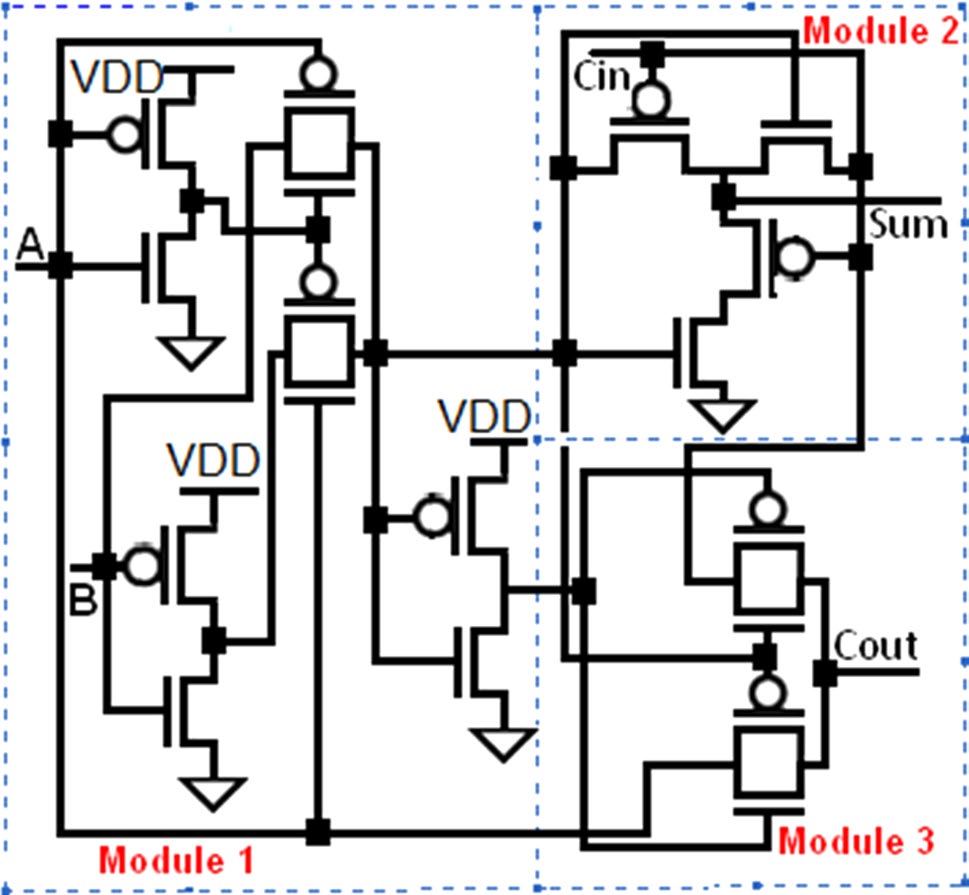
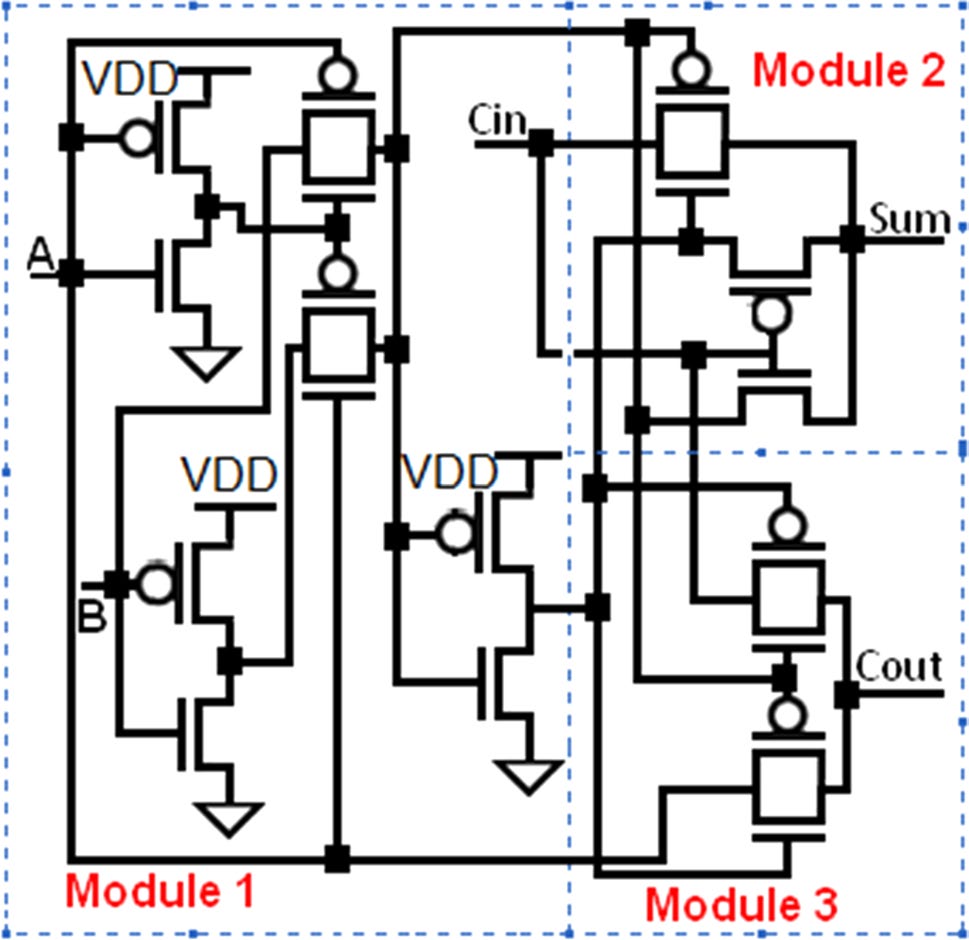
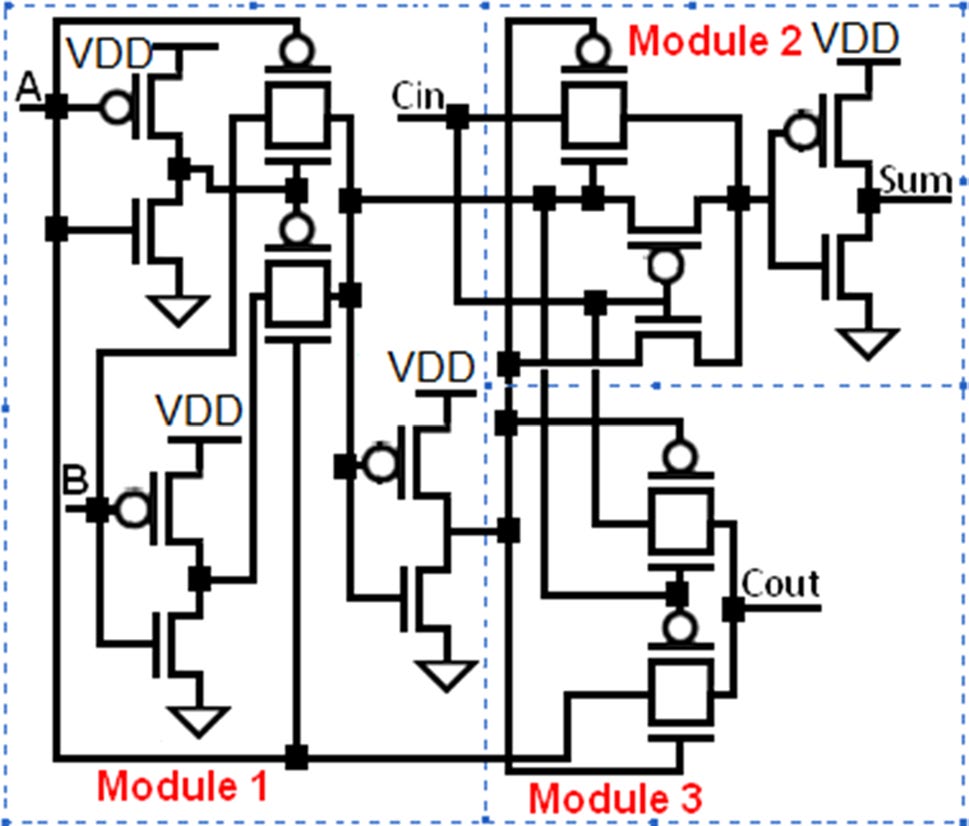
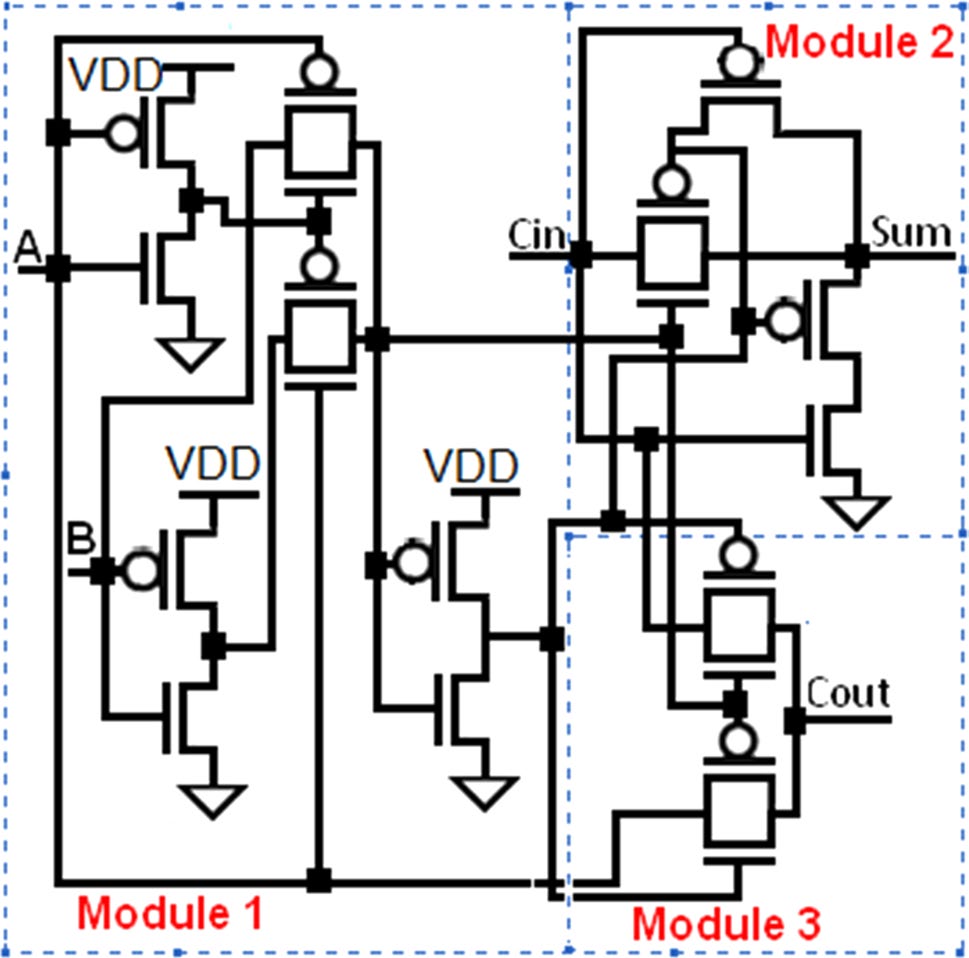
本节分析了另外五个1位全加器单元（Shams等人，2002），以证明所提出的基于FinFET的设计的优越性。这些单元由3个模块组成——第1个模块由两个反相器和两个传输门组成。该模块生成输入A和B的异或门和同或门输出。第2个模块根据第1个模块的输出和C生成和输出(S)。它也对其输入执行异或操作，即Ci和第1个模块的输出。第3个模块作为2选1多路复用器，基于输入A、CO以及第1个模块的输出生成进位输出(Ci)。模块1和模块3在所有五个全加器单元中是共用的。模块2则因不同的全加器单元而异。单元格‐1的模块2（见图11）采用6个设计使用传输门理论的晶体管。该模块的缺点是需要模块1提供互补输出，且其驱动能力差。单元格‐2的模块2（见图12）由4个晶体管构成，它不需要模块1提供互补输出即可生成和输出(S)。单元格‐3的模块2（见图13）也使用4个晶体管。该单元基于传输函数设计，且不需要Ci的补码。单元格‐4的模块2（见图14）增加了一个反相器以提高驱动能力，但导致晶体管数量增加。单元格‐5的模块2（见图15）使用5个晶体管来生成和。

单元格‐1（见图11）是基于20‐T（20个晶体管）传输门(TG)的1位全加器。与提出的基于FinFET的设计相比，该单元格的平均功耗高出(28.48×)，传播延迟长(1.59×)，PDP高出(542.7×)。单元格‐2是如图12所示的基于18‐T传输门(TG)的1位全加器。与提出的基于FinFET的设计相比，该单元格的平均功耗高出(19.52×)，传播延迟长(1.03×)，PDP高出(20.1×)。单元格‐3（见图13）是基于18‐T传输门(TG)的1位全加器。该单元格的平均功耗高出(22.21×)，传播延迟长(16.55×)，PDP高出(367.7×)，与提出的基于FinFET的设计相比。单元格‐4是如图14所示的基于20‐T传输门(TG)的1位全加器。与提出的基于FinFET的设计相比，该单元格的平均功耗高出(32.76×)，传播延迟长(4.18×)，PDP高出(135.98×)。单元格‐5（见图15）是基于20‐T传输门(TG)的1位全加器。与提出的基于FinFET的设计相比，该单元格的平均功耗高出(11.33×)，传播延迟长(2.02×)，PDP高出(4.44×)。

对传播延迟、平均功耗和功耗延迟积等设计指标进行了变异性分析，且表中列出了相应数值，见表4。可以看出，所提出的基于FinFET的设计在平均功耗、传播延迟的变异性方面分别具有8.68×、1.1×和9.41×的改善与单元格‐1相比，延迟和功耗延迟积分别得到改善。基于FinFET的设计在平均功耗、传播延迟和功耗延迟积的变异性方面分别比单元格‐2提高了8.46×、40.46×和8.20×。据观察，提出的基于FinFET的设计在平均功耗、传播延迟和功耗延迟积的变异性方面分别比单元格‐3提高了8.33×、9.08×和8.75×。基于FinFET的设计在平均功耗、传播延迟和功耗延迟积的变异性方面分别比单元格‐4提高了8.76×、8.11×和6.81×。据观察，提出的基于FinFET的设计在平均功耗、传播延迟和功耗延迟积的变异性方面分别比单元格‐5提高了8.43×、10.3×和8.5×。

5 工艺和电压变化对基于鳍式场效应晶体管的全加器（数字加法电路）的影响

由于持续的器件尺寸缩小，工艺参数和VDD的随机变化正给电路设计人员带来重大挑战（Bowman 2002；Borkar 2005）。工艺变化会影响纳米级器件中的多种器件参数，例如SiO2厚度（tOX）、体掺杂浓度（NA）、长度（L）和栅极宽度（W）。这些因素的变化会改变Vt，从而影响MOS器件的漏源电流（IDS）。我们可以通过在设计中采用电路级技术来缓解工艺和电压变化的影响。动态体偏置就是一种此类电路级技术。FBB（前向体偏置）和RBB（反向体偏置）等电路级技术虽然有效，但随着技术节点的缩小，其效果逐渐减弱（Tschanz 2002）。

由于全加器单元是算术逻辑单元的重要构成模块，因此在平均功耗（Pavg）和传播延迟方面的优化是必要且有益的。在超深亚微米（UDSM）技术中，使其对工艺和电压变化具有更强的鲁棒性显得更为重要和关键。

本文提出了一种基于FinFET的静态CMOS 1位全加器单元，能够实现更好的抗变异性。比较分析假设工艺和电压存在10%的变化。我们使用SPICE平台，基于32纳米预测技术模型参数并采用高斯分布进行蒙特卡洛分析。

平均功耗（Pavg）、传播延迟（tp）以及功耗延迟积（PDP）的百分比变异性已计算并列于表4中。所有数值均相对于FinFET进行归一化处理，归一化后的数值在括号中给出。从表4可以看出，我们提出的基于FinFET的全加器单元在VDD = 0.55 V时功耗变异性改善了3.20×，延迟变异性改善了4.70×，以及PDP变异性改善了3.35×，此外还具有更小的tp和PDP。基于FinFET的全加器单元在其设计指标上表现出比传统基于MOSFET的全加器单元更窄的分布，这是因为其减小了短沟道效应。

表4	针对所考虑的各种数字加法电路，在功耗、延迟和功耗延迟积（PDP）变异性（定义为设计指标的标准差与均值比 (σ/μ)）方面的比较
全加器单元	% 变异性 (σ/μ) @VDD = 0.55 V
	平均功耗
基于MOSFET	25.37 (3.20)
基于FinFET	7.94 (1)
单元格‐1	68.99 (8.68)
单元格‐2	67.20 (8.46)
单元格‐3	66.20 (8.33)
单元格‐4	69.60 (8.76)
单元格‐5	67.0 (8.43)

6 结论

本文分析了静态CMOS全加器，并提出了其基于FinFET的实现方案。我们还对五种基于CMOS的全加器单元进行了分析，并将其结果与提出的基于FinFET的设计进行比较。我们观察到，所提出的基于FinFET的设计具有更高的开关速度。同时发现，在相同的VDD下，我们的设计相较于基于MOSFET的全加器单元能效更高。此外，相对于工艺和电压变化，本设计在功耗、传播延迟以及功耗延迟积方面表现出更小的波动范围。因此，由于FinFET本身相比MOSFET对工艺和电压变化具有更强的免疫力，基于MOSFET的数字加法电路可有效采用FinFET实现，以获得更稳健的设计。