结构体内存对齐规则（如何计算结构体大小）_结构体中对齐是对其后一个变量的大小吗-CSDN博客

本文详细解析了结构体内存对齐的规则及其原因，并通过两个案例进行了具体说明。介绍了如何计算结构体的大小，解释了内存对齐背后的性能考量及平台移植性问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

假设我们要计算下面这个结构体的大小，你或许觉得大小难道不是 1+4+1=6 吗，实际上结构体对象的计算方式并不是直接计算的，需要遵循结构体内存对齐规则，至于为什么要这样做？原因放到最后再说。

struct Data
{
 char c1;
 int i;
 char c2;
};

结构体内存对齐规则有四点，前三点是常规结构体的计算方式，最后一点是结构体内部嵌套了一个结构体才会用上。下面就通过两个案例来了解结构体内存对齐规则。

一、案例一：简单结构体大小计算

1、第一个成员放置

案例一就是计算最开始抛出的结构体大小。结构体内存对齐规则：第一点，第一个成员要放在与结构体起始位置偏移量为0的位置。

即确定结构体的第一个成员的位置。我们从起始位置开始放，偏移量为0，也就是说，结构体的第一个成员就放在第 0 个位置。

2、第二个成员放置

结构体内存对齐规则：第二点，结构体成员从第二个成员开始，要放在偏移量为对齐数的整数倍处。

其中，对齐数 = 编译器默认对齐数和变量自身大小的较小值。默认对齐数是由编译器决定的

— VS 编译器：默认对齐数为8，对齐数 = min{8，变量自身大小}

— Linux：无默认对齐数，对齐数 = 变量自身大小

假设我们现在使用的是VS的编译器，结构体第二个成员是 int 类型，自身大小为 4，所以对齐数 = min{4,8} = 4。那么偏移量就是4的整数倍，我们先看第 4 个位置有没有被占据，没有被占据，那就从第 4 个位置开始放。

3、第三个成员放置

第三个结构体成员的放置方式和第二个成员一样，第三个结构体成员为 char 类型，自身大小为1，对齐数 = min{1，8} = 1，此时偏移量应该为1的倍数，8 是 1的倍数，所以此时 c2 应该放在第 8 个位置上。

还没有结束，接下来就要用到结构体内存对齐原则的第三点了，结构体内存对齐规则：第三点，结构体的最终大小必须是所有成员的对齐数中最大值的整数倍。

struct Data
{       
 char c1;      //1 8 -> 1 (自身大小  默认对齐数  ->  对齐数)
 int i;        //4 8 -> 4
 char c2;      //1 8 -> 1
//char c3[5]   //对齐数是 1。其实就是依次放5个char类型的数据，因此放的时候，每次只关注一个，对齐数就是1
};

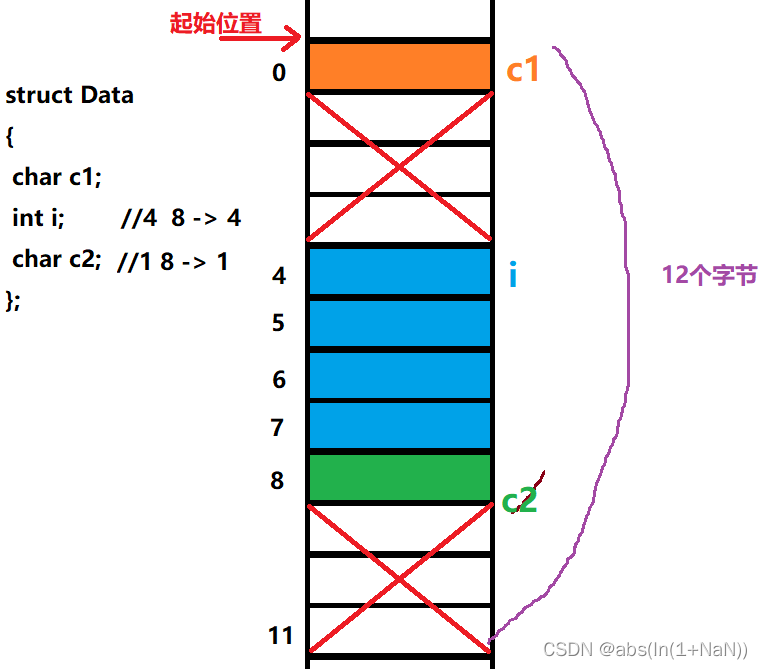
三个结构体成员的对齐数依次是1、4 、1，三个对齐数里的最大值为 4，即结构体的最终大小必须是 4 的整数倍，从上面排布的结果来看，当前的字节数为 9 ，因此，需要补全为12 个字节，其实就相当于浪费了3个字节。下面这个才是一个结构体的最终大小。

4、代码验证

至于这个结构体的大小到底是不是 12，我们可以通过代码验证一下。

二、案例二：复杂结构体计算（嵌套结构体）

一个结构体中是可以嵌套其他结构体的，现在我们要计算结构体Combine的大小，又该如何计算呢？？这里就需要用到结构体内存对齐规则的第四点了。

struct Data
{
	char c1;      //1 8 -> 1 (自身大小  默认对齐数  ->  对齐数)
	int i;        //4 8 -> 4
	char c2;      //1 8 -> 1
};

struct Combine
{
	char c3;          //1 8 -> 1 (自身大小  默认对齐数  ->  对齐数)
	struct Data d1;   //       4
	double d2;        //8 8 -> 8
};

结构体内存对齐规则：第四点，如果嵌套了结构体的情况，嵌套的结构体的偏移量是自己成员最大对齐数的整数倍，构体的整体大小就是最大对齐数（含嵌套结构体的对齐数）的整数倍。