优先级队列priority_queue模拟实现（含堆排向下、向上调整、仿函数）

优先级队列priority_queue也是队列的一种，可以理解为是排好序的队列，每增加一个数，内部就会自动排序，底层实现是通过堆排序实现的

图中可以发现，默认使用的容器是vector，既然底层是使用堆排序，那就需要频繁的通过下标访问，根据前面的了解，deque的访问速度是远不如vector的。less是仿函数，less是建大堆，可以更改仿函数让内部变成建小堆。

---

目录

一、向上、向下调整（默认建大堆）

1、向上调整

2、向下调整

二、优先级队列priority_queue模拟实现

1、size()：队列中元素的个数

2、empty()：判断队列是否为空

3、front()：返回根元素

4、push_back()：尾插

 5、pop_back()：头删（删除根节点）

6、测试

 三、优先级队列priority_queue模拟实现优化

1、仿函数

2、优先级队列priority_queue模拟实现优化

---

一、向上、向下调整（默认建大堆）

1、向上调整

当我们在堆的末尾新增一个数据的时候，此时需要向上调整，核心思路是每一次都要和自己的父节点比较，如果新增数据比父节点更大，那就和父节点交换，子节点向上移动，同时计算出父节点的位置

/*
    _con[]      是存放数据的数组
    size()函数  代表数组大小
*/
void adjust_up(size_t child)                  //输入的参数是从哪个位置开始调整
{
	size_t parent = (child - 1) / 2;
	while (child > 0)                         //中止条件一：child到达根节点
	{
		if (_con[child] > _con[parent])         
		{
			swap(_con[child], _con[parent]);  //孩子结点比父节点大，则交换      
			child = parent;			          //更新子节点的位置		
			parent = (child - 1) / 2;         //重新计算父节点
		}
		else
		{
			break;                            //中止条件二：无需继续调整
		}
	}
}

2、向下调整

向下调整的核心思路是，首先选出左右孩子中更大的那个，如果没有右孩子，那就默认左孩子最大；其次让更大的孩子和父节点比较，如果比父节点大，就交换，父节点移动到下一个节点，同时计算出子节点的位置

/*
    _con[]      是存放数据的数组
    size()函数  代表数组大小
*/
void adjust_down(size_t parent)				        //输入的参数表示要从哪个位置开始向下调整
{
	size_t child = parent * 2 + 1;			        //一开始默认左孩子最大
	while (child < size())							//中止条件一：到达叶子节点
	{
		if (child + 1 < size() && _con[child] < _con[child + 1])	//默认左孩子最大，只需考虑右孩子存在而且右孩子大于左孩子
		{
			child++;
		}

		if (_con[parent] < _con[child])
		{
			swap(_con[parent], _con[child]);		//父节点比最大的孩子节点更小，则交换
			parent = child;							//更新父节点的位置
			child = parent * 2 + 1;					//重新计算子节点的位置
		}
		else
		{
			break;									//中止条件二：无需继续调整
		}
	}
}

二、优先级队列priority_queue模拟实现

下面是优先级队列的模拟实现，暂时没有加入仿函数，这里的模拟实现不支持list，如果使用迭代器是能够支持list的，但是太麻烦，用 [ ] 来的快一些。在实现之前，我们先看看priority有哪些需要实现的函数。

 下面就依次来实现这些函数，最后使用这些函数来打印优先级队列中的内容

1、size()：队列中元素的个数

size_t size()
{
	return _con.size();
}

2、empty()：判断队列是否为空

bool empty(const T& val)
{
	return _con.size() == 0;
}

3、front()：返回根元素

const T& front()
{
	return _con[0];
}

4、push_back()：尾插

void push_back(const T& val)
{
	_con.push_back(val);        //在数组末尾添加元素
	adjust_up(size() - 1);      //向上调整
}

 5、pop_back()：头删（删除根节点）

当我们pop的时候，根据队列的特性，默认是头删，也就是删除根节点，一旦删除了根节点，整个二叉树会崩溃，所以我们一般会先把根结点和最后一个结点交换，然后尾删，最后从根结点开始向下调整为大堆。

void pop_back()
{
	swap(_con[0], _con[size() - 1]);        //和最后一个节点交换
	_con.pop_back();                        //删除最后一个节点
	adjust_down(0);                         //向下调整
}

6、测试

我们使用上述实现的函数来打印优先级队列中的内容

int main()
{
	xing::priority_queue<int> pq;
	pq.push_back(3);
	pq.push_back(3);
	pq.push_back(7);
	pq.push_back(1);
	pq.push_back(9);

	while (!pq.empty())
	{
		cout << pq.front() << " ";
		pq.pop_back();
	}
	cout << endl;
	return 0;
}

 三、优先级队列priority_queue模拟实现优化

我们已经初步实现了优先级队列的一些功能，但是还剩下一个模板参数Compare没说

上面我们一直在模拟大堆的实现，但是如果我希望使用小堆实现呢？？重新修改为小堆吗，这未免有点麻烦，所以模板参数Compare就是为了解决这个问题，在那之前我们需要了解仿函数

1、仿函数

其实本质上就是重载了运算符 ()，类似于 [ ] 的重载

T& operator[](int pos);        //后面的()只是说明要用到什么参数

struct Less
{
    //不要被两个()迷惑了，第一个()才是需要用到的，第二个只是说明前面的()要填入什么参数
	bool operator()(int x, int y)
	{
		return x < y;
	}
};

int main()
{
	Less less;
	cout << less(1, 2) << endl;    
    //上面等价于  cout << less.operator()(1, 2) << endl;
}

上面的只支持int类型，我们还可以把上面的改成模板的形式

template<class T>
struct Less
{
    //不要被两个()迷惑了，第一个()才是需要用到的，第二个只是说明前面的()要填入什么参数
	bool operator()(const T& x, const T& y)
	{
		return x < y;
	}
};

2、优先级队列priority_queue模拟实现优化

现在有了仿函数，我们可以在priority_queue所属的命名空间里加上上面写的Less结构体模板以及下面的Greater结构体模板，这样的话我们就可以在建大堆和小堆之间随意切换了

template<class T>
struct Greater
{
	bool operator()(const T& x, const T& y)
	{
		return x > y;
	}
};

下面需要新增一个模板参数，同时稍微修改向上调整函数adjust_up、向下调整函数adjust_down，毕竟这两个函数决定了建大堆还是小堆

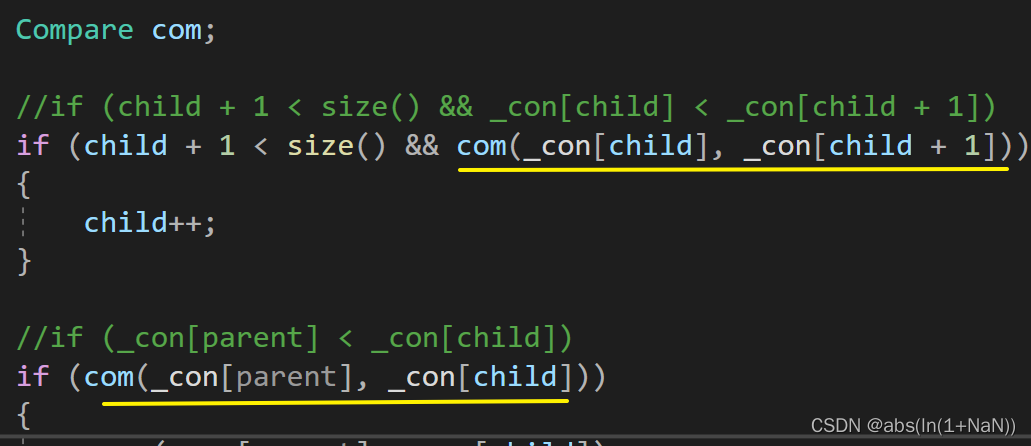
下面来依次测试一下建大堆（自上而下逐渐变小）和建小堆（自上而下逐渐变大）