归并排序（MergeSort）

Merge是左堆哪里引入的一个概念，意思是把两个堆合并成一个堆。这里我们把归并的思想引入到排序中，通过把两个已排序的数据表合并来对数据进行排序。

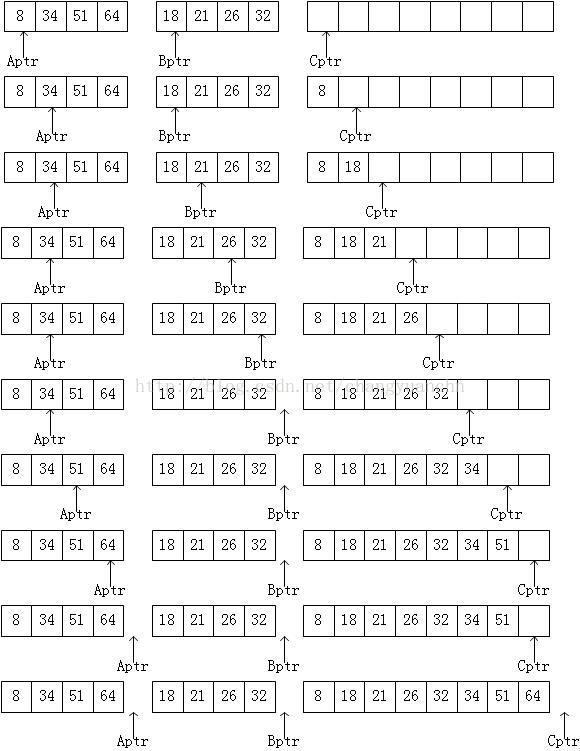
堆排序利用了递归的思想，它的最坏时间复杂度为O(NlogN)。如下图所示，

由上图可知，归并排序需要3个游标，每个游标指向数组的起始位置，通过比较A[Aptr]与B[Bptr]的大小，然后将较小的值拷贝到数组C中，然后进行相应的游标的位置移动。

如上图中，第一次归并排序，移动的游标为Aptr和Cptr。

归并排序采用递归的思想，每次把待排序数据分成两半，然后对这两份数据继续二分，直到每组都有一个数据的时候，这个时候这个数据就是以排序的了（只有一个数据，当然是排好序的了。）然后递归向上就可以得到最终的排序结果。

代码实现：

void Msort(ElementType A[],ElementType TmpArray[],int Left, int Right)
{
	int Center;
	if(Left<Right)
	{
		Center = (Left+Right)/2;
		Msort(A,TmpArray,Left,Center);
		Msort(A,TmpArray,Center+1,Right);
		Merge(A,TmpArray,Left,Center+1,Right);
	}
}

void MergeSort(ElementType A[], int N)
{
	ElementType *TmpArray;
	TmpArray = malloc(N*sizeof(ElementType));
	if(TmpArray != NULL)
	{
		Msort(A,TmpArray,0,N-1)
			free(TmpArray);
	}
	else
		Error("Out of Spaces!!");
}
void Merge(ElementType A[],ElementType TmpArray[],int Lpos, int Rpos,int RightEnd)
{
	int i,TmpPos,LeftEnd,NumElements;
	LeftEnd = Rpos-1;
	TmpPos = Lpos;
	NumElements = RightEnd-Lpos+1;
	while(Lpos<LeftEnd && Rpos<RightEnd)
		if(A[Lpos]<=A[Rpos])
			TmpArray[TmpPos++] = A[Lpos++];
		else
			TmpArray[TmpPos++] = A[Rpos++];

	while(Lpos<=LeftEnd)//Copy rest of first half
		TmpArray[TmpPos++] = A[Lpos++];
	while(Lpos<=RightEnd)//Copy rest of second half
		TmpArray[TmpPos++] = A[Rpos++];

	//Copy TmpArray Back
	for(i=0;i<NumElements;i++,RightEnd--)
		A[RightEnd] = TmpArray[RightEnd];
}

归并排序的缺点应该是需要额外的内存。因为它需要一个新的数组来存储排序的数据。而且虽然时间复杂度比较小，为O（NlogN）,但是由于程序中需要进行数据的拷贝，因此比较耗时，因此，运行归并排序的实际时间并不比其他的算法要好多少。而其实归并排序更多的用于外部排序中。