网络流（Network Flow）

0） 引论

网络流问题是有实际应用来源的。个人觉得网络流应该是网络流量的意思，它限制了一个网络的最大流量问题。举个例子，对于一个给水网络，每条管道的最大流量是确定的，这就要求我们解决整个给水网络的流量问题；或者是交通网络，可以对每条道路的交通流量进行计算，使其不能超多最大的道路流量。

1） 数学模型

对于一个网络流我们可以用一个有向图G = （V，E，C）表示；V表示顶点的集合，E表示有向边的集合，C表示有向边的最大流量。对于每一个网络，有一个源输入点，称之为source，一个输出点，称之为sink。在不是出发点source也不是输出点sink的其他点，流量不能超过有向边的最大流量，这是一个约束条件。

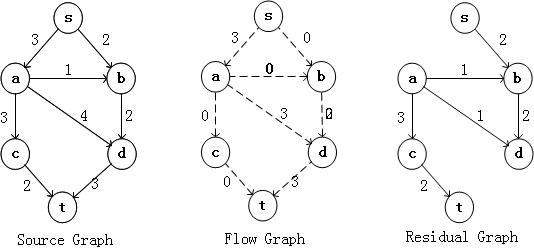
下图就是一个简单的网络流模型：

2） 最大流问题

网络流的一个问题就是：最大流问题。最大流问题要求解决从source到sink能通过的最大的流量

我们下面来介绍一种简单的放法来解决这一问题。

首先我们需要引入几个概念。

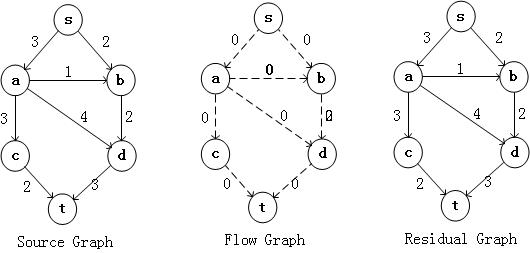
我们称呼上面的图为原始图G；然后我们需要构建一个流图（Flow Graph）Gf，流图是我么算法用的图，最初为流量全部为0的图；最后G - Gf得到Gr，也就是残余图，如下图所示：

首先我们需要在Residual Graph中找到一个点s到点t的路径，假设为s,a,c,t，则在FLow Graph图上标示出来。

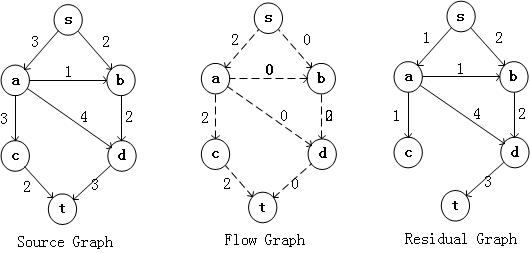
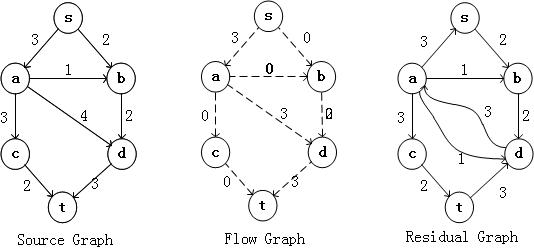
然后继续在Residual Graph中找到一个点s到点t的路径，假设为s,b,d,t，得到下面的结果

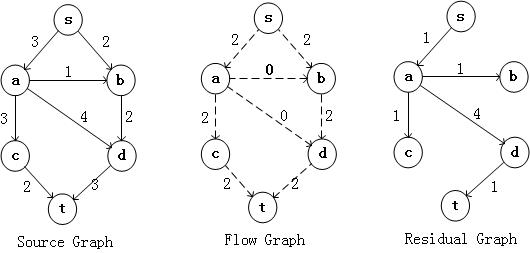
然后继续在Residual Graph中找到一个点s到点t的路径，为s,a,d,t，得到下面的结果

现在在Residual Graph中已经不存在从s到t的路径，因此网络的流图为Flow Graph，它模拟了网络中的流量。因此可以很方便的得到从Source到sink的最大流量为5 。

当然这里的例子只是巧合可以看到从s的两条输出为5，这跟网络的最大流没有什么关系，不是输入为5输出就是5，这只是一个例子上的巧合

3） 最大流算法的改进

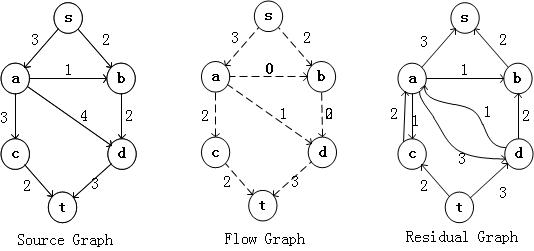
上面的算法很简单，但是这个算法是有一点点小的缺陷的。如下面的例子所示

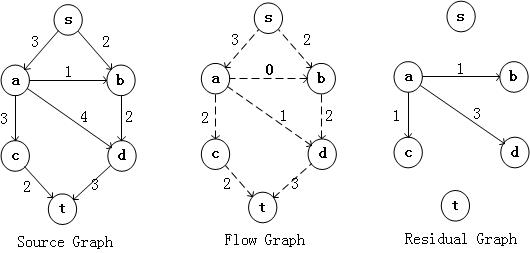
假设我们取得路径是s,a,d,t；那么就有问题了，从S到t已经没有路径了，而这明显不是最终的结果，因此需要对方法进行改进。

改进的方法是：每当我们选择了一个路径后，都要在Residual Graph中标示一个反方向的路径，后面的路径选取可以利用这些反向的路径

然后继续在Residual Graph中找到一个点s到点t的路径，为s,b,d,a,c,t，得到下面的结果

现在在Residual Graph中已经不存在从s到t的路径。改进后的方法具有较强的适应性。