考察数据结构
<script type="text/javascript">function StorePage(){d=document;t=d.selection?(d.selection.type!='None'?d.selection.createRange().text:''):(d.getSelection?d.getSelection():'');void(keyit=window.open('http://www.365key.com/storeit.aspx?t='+escape(d.title)+'&u='+escape(d.location.href)+'&c='+escape(t),'keyit','scrollbars=no,width=475,height=575,left=75,top=20,status=no,resizable=yes'));keyit.focus();}</script>
本文是介绍在.Net平台下使用数据结构的系列文章,共分为六部分,这是本文的第一部分.本文试图考察几种数据结构,其中有的包含在.Net Framework的基类库中,有的是我们自己创建的.如果你对这些名词不太熟悉,那么我们可以把数据结构看作是一种抽象结构或是类,它通常用来组织数据,并提供对数据的操作.最常见并为我们所熟知的数据结构就是数组array,它包含了一组连续的数据,并通过索引进行访问.
数据结构性能分析
using System.Collections;
using System.IO;
{
public static void Main()
{
string [] fs = Directory.GetFiles(@"C:/Inetpub/wwwroot");
bool foundXML = false;
int i = 0;
for (i = 0; i < fs.Length; i++)
if (String.Compare(Path.GetExtension(fs[i]), ".xml", true) == 0)
{
foundXML = true;
break;
}
if (foundXML)
Console.WriteLine("XML file found - " + fs[i]);
else
Console.WriteLine("No XML files found.");
}
}
现在我们来看看最糟糕的一种情况,当这个列表中不存在XML文件或者XML文件是在列表的最后,我们将会搜索完这个数组的所有元素.再来分析一下数组的效率,我们必须问问自己,"假设数组中现有n个元素,如果我添加一个新元素,增长为n+1个元素,那么新的运行时间是多少?(术语"运行时间"--running time,不能顾名思义地认为是程序运行所消耗的绝对时间,而指的是程序完成该任务所必须执行的步骤数.以数组而言,运行时间特定被认为是访问数组元素所需执行的步骤数。)要搜索数组中的一个值,潜在的可能是访问数组的每一个元素,如果数组中有n+1个元素,就将执行n+1次检查。那就是说,搜索数组耗费的时间与数组元素个数成几何线形比。
2、找到符合计算运行时间条件的代码行。在这些行上面置1。
3、判断这些置1的行是否包含在循环中,如果是,则将1改为1乘上循环执行的最大次数。如果嵌套两重或多重循环,继续对循环做相同的乘法。
4、找到对每行写下的最大值,它就是运行时间。
注:
1.数组的数据存储在一段连续的内存之中;
2.数组的所有元素都必须是同一种数据类型,因此数组又被认为是单一数据结构(homogeneous data structures);
3.数组元素可以直接访问。(在很多数据结构中,这一特点是不必要的。例如,文章第四部分介绍的数据结构SkipList。要访问SkipList中的特定元素,你必须根据搜索其他元素直到找到搜索对象为止。然而对于数组而言,如果你知道你要查找第i个元素,就可以通过arrayName[i]来访问它。)(译注:很多语言都规定数组的下标从0开始,因此访问第i个元素,应为arrayName[i-1])
1.分配空间
2.数据访问
3.数组空间重分配(Redimensioning)
FileInfo [] files;
files = new FileInfo[10];
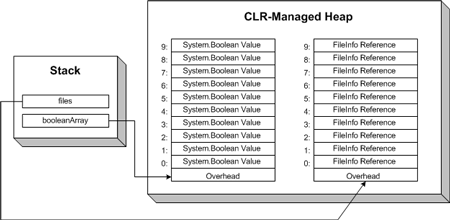
图一:在托管堆中顺序存放数组元素
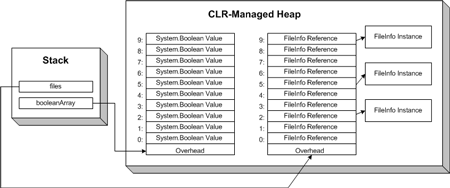
图二:在托管堆中顺序存放数组元素
.Net中所有数组都支持对元素的读写操作。访问数组元素的语法格式如下:
bool b = booleanArray[7];
booleanArray[0] = false;
using System.Collections;
{
public static void Main()
{
// 创建包含3个元素的int类型数组
int [] fib = new int[3];
fib[0] = 1;
fib[1] = 1;
fib[2] = 2;
// 重新分配数组,长度为10
int [] temp = new int[10];
fib.CopyTo(temp, 0);
// 将临时数组赋给fib
fib = temp;
}
}
countDown.Add(5);
countDown.Add(4);
countDown.Add(3);
countDown.Add(2);
countDown.Add(1);
countDown.Add("blast off!");
countDown.Add(new ArrayList());
int x = (int) countDown[0];
string y = (string) countDown[5];
countDown[1] = 5;
countDown[7] = 5;
本文是"考察数据结构"系列文章的第二部分,考察了三种研究得最多的数据结构:队列(Queue),堆栈(Stack)和哈希表(Hashtable)。正如我们所知,Quenu和Stack其实一种特殊的ArrayList,提供大量不同类型的数据对象的存储,只不过访问这些元素的顺序受到了限制。Hashtable则提供了一种类数组(array-like)的数据抽象,它具有更灵活的索引访问。数组需要通过序数进行索引,而Hashtable允许通过任何一种对象索引数据项。
目录:
简介
“排队顺序”的工作进程
“反排队顺序”——堆栈数据结构
序数索引限制
System.Collections.Hashtable类
结论
简介
在第一部分中,我们了解了什么是数据结构,评估了它们各自的性能,并了解了选择何种数据结构对特定算法的影响。另外我们还了解并分析了数据结构的基础知识,介绍了一种最常用的数据结构:数组。
数组存储了同一类型的数据,并通过序数进行索引。数组实际的值是存储在一段连续的内存空间中,因此读写数组中特定的元素非常迅速。
因其具有的同构性及定长性,.Net Framework基类库提供了ArrayList数据结构,它可以存储不同类型的数据,并且不需要显式地指定长度。前文所述,ArrayList本质上是存储object类型的数组,每次调用Add()方法增加元素,内部的object数组都要检查边界,如果超出,数组会自动以倍数增加其长度。
第二部分,我们将继续考察两种类数组结构:Queue和Stack。和ArrayList相似,他们也是一段相邻的内存块以存储不同类型的元素,然而在访问数据时,会受到一定的限制。
之后,我们还将深入了解Hashtable数据结构。有时侯,我们可以把Hashtable看作杀一种关联数组(associative array),它同样是存储不同类型元素的集合,但它可通过任意对象(例如string)来进行索引,而非固定的序数。
“排队顺序”的工作进程
如果你要创建不同的服务,这种服务也就是通过多种资源以响应多种请求的程序;那么当处理这些请求时,如何决定其响应的顺序就成了创建服务的一大难题。通常解决的方案有两种:
“排队顺序”原则
“基于优先等级”的处理原则
当你在商店购物、银行取款的时候,你需要排队等待服务。“排队顺序”原则规定排在前面的比后面的更早享受服务。而“基于优先等级”原则,则根据其优先等级的高低决定服务顺序。例如在医院的急诊室,生命垂危的病人会比病情轻的更先接受医生的诊断,而不用管是谁先到的。
设想你需要构建一个服务来处理计算机所接受到的请求,由于收到的请求远远超过计算机处理的速度,因此你需要将这些请求按照他们递交的顺序依此放入到缓冲区中。
一种方案是使用ArrayList,通过称为nextJobPos的整型变量来指定将要执行的任务在数组中的位置。当新的工作请求进入,我们就简单使用ArrayList的Add()方法将其添加到ArrayList的末端。当你准备处理缓冲区的任务时,就通过nextJobPos得到该任务在ArrayList的位置值以获取该任务,同时将nextJobPos累加1。下面的程序实现该算法:
using System;
using System.Collections;
public class JobProcessing
{
private static ArrayList jobs = new ArrayList();
private static int nextJobPos = 0;
public static void AddJob(string jobName)
{
jobs.Add(jobName);
}
public static string GetNextJob()
{
if (nextJobPos > jobs.Count - 1)
return "NO JOBS IN BUFFER";
else
{
string jobName = (string) jobs[nextJobPos];
nextJobPos++;
return jobName;
}
}
public static void Main()
{
AddJob("1");
AddJob("2");
Console.WriteLine(GetNextJob());
AddJob("3");
Console.WriteLine(GetNextJob());
Console.WriteLine(GetNextJob());
Console.WriteLine(GetNextJob());
Console.WriteLine(GetNextJob());
AddJob("4");
AddJob("5");
Console.WriteLine(GetNextJob());
}
}
输出结果如下:
1
2
3
NO JOBS IN BUFFER
NO JOBS IN BUFFER
4
这种方法简单易懂,但效率却可怕得难以接受。因为,即使是任务被添加到buffer中后立即被处理,ArrayList的长度仍然会随着添加到buffer中的任务而不断增加。假设我们从缓冲区添加并移除一个任务需要一秒钟,这意味一秒钟内每调用AddJob()方法,就要调用一次ArrayList的Add()方法。随着Add()方法持续不断的被调用,ArrayList内部数组长度就会根据需求持续不断的成倍增长。五分钟后,ArrayList的内部数组增加到了512个元素的长度,这时缓冲区中却只有不到一个任务而已。照这样的趋势发展,只要程序继续运行,工作任务继续进入,ArrayList的长度自然会继续增长。
出现如此荒谬可笑的结果,原因是已被处理过的旧任务在缓冲区中的空间没有被回收。也即是说,当第一个任务被添加到缓冲区并被处理后,此时ArrayList的第一元素空间应该被再利用。想想上述代码的工作流程,当插入两个工作——AddJob("1")和AddJob("2")后——ArrayList的空间如图一所示:
图一:执行前两行代码后的ArrayList
注意这里的ArrayList共有16个元素,因为ArrayList初始化时默认的长度为16。接下来,调用GetNextJob()方法,移走第一个任务,结果如图二:

图二:调用GetNextJob()方法后的ArrayList
当执行AddJob(“3”)时,我们需要添加新任务到缓冲区。显然,ArrayList的第一元素空间(索引为0)被重新使用,此时在0索引处放入了第三个任务。不过别忘了,当我们执行了AddJob(“3”)后还执行了AddJob(“4”),紧接着用调用了两次GetNextJob()方法。如果我们把第三个任务放到0索引处,则第四个任务会被放到索引2处,问题发生了。如图三:
图三:将任务放到0索引时,问题发生
现在调用GetNextJob(),第二个任务从缓冲中移走,nextJobPos指针指向索引2。因此,当再一次调用GetNextJob()时,第四个任务会先于第三个被移走,这就有悖于与我们的“排序顺序”原则。
问题发生的症结在于ArrayList是以线形顺序体现任务列表的。因此我们需要将新任务添加到就任务的右恻以保证当前的处理顺序是正确的。不管何时到达ArrayList的末端,ArrayList都会成倍增长。如果产生产生未被使用的元素,则是因为调用了GetNextJob()方法。
解决之道是使我们的ArrayList成环形。环形数组没有固定的起点和终点。在数组中,我们用变量来维护数组的起止点。环形数组如图四所示:

图四:环形数组图示
在环形数组中,AddJob()方法添加新任务到索引endPos处(译注:endPos一般称为尾指针),之后“递增”endPos值。GetNextJob()方法则根据头指针startPos获取任务,并将头指针指向null,且“递增”startPos值。我之所以把“递增”两字加上引号,是因为这里所说的“递增”不仅仅是将变量值加1那么简单。为什么我们不能简单地加1呢?请考虑这个例子:当endPos等于15时,如果endPos加1,则endPos等于16。此时调用AddJob(),它试图去访问索引为16的元素,结果出现异常IndexOutofRangeException。
事实上,当endPos等于15时,应将endPos重置为0。通过递增(increment)功能检查如果传递的变量值等于数组长度,则重置为0。解决方案是将变量值对数组长度值求模(取余),increment()方法的代码如下:
int increment(int variable)
{
return (variable + 1) % theArray.Length;
}
注:取模操作符,如x % y,得到的是x 除以 y后的余数。余数总是在0 到 y-1之间。
这种方法好处就是缓冲区永远不会超过16个元素空间。但是如果我们要添加超过16个元素空间的新任务呢?就象ArrayList的Add()方法一样,我们需要提供环形数组自增长的能力,以倍数增长数组的长度。
System.Collection.Queue类
就象我们刚才描述的那样,我们需要提供一种数据结构,能够按照“排队顺序”的原则插入和移除元素项,并能最大化的利用内存空间,答案就是使用数据结构Queue。在.Net Framework基类库中已经内建了该类——System.Collections.Queue类。就象我们代码中的AddJob()和GetNextJob()方法,Queue类提供了Enqueue()和Dequeue()方法分别实现同样的功能。
Queue类在内部建立了一个存放object对象的环形数组,并通过head和tail变量指想该数组的头和尾。默认状态下,Queue初始化的容量为32,我们也可以通过其构造函数自定义容量。既然Queue内建的是object数组,因此可以将任何类型的元素放入队列中。
Enqueue()方法首先判断queue中是否有足够容量存放新元素。如果有,则直接添加元素,并使索引tail递增。在这里tail使用求模操作以保证tail不会超过数组长度。如果空间不够,则queue根据特定的增长因子扩充数组容量。增长因子默认值为2.0,所以内部数组的长度会增加一倍。当然你也可以在构造函数中自定义该增长因子。
Dequeue()方法根据head索引返回当前元素。之后将head索引指向null,再“递增”head的值。也许你只想知道当前头元素的值,而不使其输出队列(dequeue,出列),则Queue类提供了Peek()方法。
Queue并不象ArrayList那样可以随机访问,这一点非常重要。也就是说,在没有使前两个元素出列之前,我们不能直接访问第三个元素。(当然,Queue类提供了Contains()方法,它可以使你判断特定的值是否存在队列中。)如果你想随机的访问数据,那么你就不能使用Queue这种数据结构,而只能用ArrayList。Queue最适合这种情况,就是你只需要处理按照接收时的准确顺序存放的元素项。
注:你可以将Queues称为FIFO数据结构。FIFO意为先进先出(First In, First Out),其意等同于“排队顺序(First come, first served)”。
译注:在数据结构中,我们通常称队列为先进先出数据结构,而堆栈则为先进后出数据结构。然而本文没有使用First in ,first out的概念,而是first come ,first served。如果翻译为先进先服务,或先处理都不是很适合。联想到本文在介绍该概念时,以商场购物时需要排队为例,索性将其译为“排队顺序”。我想,有排队意识的人应该能明白其中的含义吧。那么与之对应的,对于堆栈,只有名为“反排队顺序”,来代表(First Come, Last Served)。希望各位朋友能有更好地翻译来取代我这个拙劣的词语。为什么不翻译为“先进先出”,“先进后出”呢?我主要考虑到这里的英文served,它所包含的含义很广,至少我们可以将其认为是对数据的处理,因而就不是简单地输出那么简单。所以我干脆避开这个词语的含义。
“反排队顺序”——堆栈数据结构
Queue数据结构通过使用内部存储object类型的环形数组以实现“排队顺序”的机制。Queue提供了Enqueue()和Dequeue()方法实现数据访问。“排队顺序”在处理现实问题时经常用到,尤其是提供服务的程序,例如web服务器,打印队列,以及其他处理多请求的程序。
在程序设计中另外一个经常使用的方式是“反排队顺序(first come,last served)”。堆栈就是这样一种数据结构。在.Net Framework基类库中包含了System.Collection.Stack类,和Queue一样,Stack也是通过存储object类型数据对象的内部环形数组来实现。Stack通过两种方法访问数据——Push(item),将数据压入堆栈;Pop()则是将数据弹出堆栈,并返回其值。
一个Stack可以通过一个垂直的数据元素集合来形象地表示。当元素压入堆栈时,新元素被放到所有其他元素的顶端,弹出时则从堆栈顶端移除该项。下面两幅图演示了堆栈的压栈和出栈过程。首先按照顺序将数据1、2、3压入堆栈,然后弹出:

图五:向堆栈压入三个元素

图六:弹出所有元素后的Stack
注意Stack类的缺省容量是10个元素,而非Queue的32个元素。和Queue和ArrayList一样,Stack的容量也可以根据构造函数定制。如同ArrayList,Stack的容量也是自动成倍增长。(回忆一下:Queue可以根据构造函数的可选项设置增长因子。)
注:Stack通常被称为“LIFO先进后出”或“LIFO后进先出”数据结构。
堆栈:计算机科学中常见的隐喻
现实生活中有很多同Queue相似的例子:DMV(译注:不知道其缩写,恕我孤陋寡闻,不知其意)、打印任务处理等。然而在现实生活很难找到和Stack近似的范例,但它在各种应用程序中却是一种非常重要的数据结构。
设想一下我们用以编程的计算机语言,例如:C#。当执行C#程序时,CLR(公共语言运行时)将调用Stack以跟踪功能模块(译注:这里原文为function,我理解作者的含义不仅仅代表函数,事实上很多编译器都会调用堆栈以确定其地址)的执行情况。每当调用一个功能模块,相关信息就会压入堆栈。调用结束则弹出堆栈。堆栈顶端数据为当前调用功能的信息。(如要查看功能调用堆栈的执行情况,可以在Visual Studio.Net下创建一个项目,设置断点(breakpoint),在执行调试。当执行到断点时,会在调试窗口(Debug/Windows/Call Stack)下显示堆栈信息。
序数索引的限制
我们在第一部分中讲到数组的特点是同种类型数据的集合,并通过序数进行索引。即:访问第i个元素的时间为定值。(请记住此种定量时间被标记为O(1)。)
也许我们并没有意识到,其实我们对有序数据总是“情有独钟”。例如员工数据库。每个员工以社保号(social security number)为其唯一标识。社保号的格式为DDD-DD-DDDD(D的范围为数字0——9)。如果我们有一个随机排列存储所有员工信息的数组,要查找社保号为111-22-3333的员工,可能会遍历数组的所有元素——即执行O(n)次操作。更好的办法是根据社保号进行排序,可将其查找时间缩减为O(log n)。
理想状态下,我们更愿意执行O(1)次时间就能查找到某员工的信息。一种方案是建立一个巨型的数组,以实际的社保号值为其入口。这样数组的起止点为000-00-0000到999-99-9999,如下图所示:

图七:存储所有9位数数字的巨型数组
如图所示,每个员工的信息都包括姓名、电话、薪水等,并以其社保号为索引。在这种方式下,访问任意一个员工信息的时间均为定值。这种方案的缺点就是空间极度的浪费——共有109,即10亿个不同的社保号。如果公司只有1000名员工,那么这个数组只利用了0.0001%的空间。(换个角度来看,如果你要让这个数组充分利用,也许你的公司不得不雇佣全世界人口的六分之一。)
用哈希函数压缩序数索引
显而易见,创建10亿个元素数组来存储1000名员工的信息是无法接受的。然而我们又迫切需要提高数据访问速度以达到一个常量时间。一种选择是使用员工社保号的最后四位来减少社保号的跨度。这样一来,数组的跨度只需要从0000到9999。图八显示了压缩后的数组。

图八:压缩后的数组
此方案既保证了访问耗时为常量值,又充分利用了存储空间。选择社保号的后四位是随机的,我们也可以任意的使用中间四位,或者选择第1、3、8、9位。
在数学上将这种9位数转换为4位数成为哈希转换(hashing)。哈希转换可以将一个索引器空间(indexers space)转换为哈希表(hash table)。
哈希函数实现哈希转换。以社保号的例子来说,哈希函数H()表示为:
H(x) = x 的后四位
哈希函数的输入可以是任意的九位社保号,而结果则是社保号的后四位数字。数学术语中,这种将九位数转换为四位数的方法称为哈希元素映射,如图九所示:

图九:哈希函数图示
图九阐明了在哈希函数中会出现的一种行为——冲突(collisions)。即我们将一个相对大的集合的元素映射到相对小的集中时时,可能会出现相同的值。例如社保号中所有后四位为0000的均被映射为0000。那么000-99-0000,113-14-0000,933-66-0000,还有其他的很多都将是0000。
看看之前的例子,如果我们要添加一个社保号为123-00-0191的新员工,会发生什么情况?显然试图添加该员工会发生冲突,因为在0191位置上已经存在一个员工。
数学标注:哈希函数在数学术语上更多地被描述为f:A->B。其中|A|>|B|,函数f不是一一映射关系,所以之间会有冲突。
显然冲突的发生会产生一些问题。在下一节,我们会看看哈希函数与冲突发生之间的关系,然后简单地犯下处理冲突的几种机制。接下来,我们会将注意力放在System.Collection.Hashtable类,并提供一个哈希表的实现。我们会了解有关Hashtable类的哈希函数,冲突解决机制,以及一些使用Hashtable的例子。
避免和解决冲突
当我们添加数据到哈希表中,冲突是导致整个操作被破坏的一个因素。如果没有冲突,则插入元素操作成功,如果发生了冲突,就需要判断发生的原因。由于冲突产生提高了代价,我们的目标就是要尽可能将冲突压至最低。
哈希函数中冲突发生的频率与传递到哈希函数中的数据分布有关。在我们的例子中,假定社保号是随机分配的,那么使用最后四位数字是一个不错的选择。但如果社保号是以员工的出生年份或出生地址来分配,因为员工的出生年份和地址显然都不是均匀分配的,那么选用后四位数就会因为大量的重复而导致更大的冲突。
注:对于哈希函数值的分析需要具备一定的统计学知识,这超出了本文讨论的范围。必要地,我们可以使用K维(k slots)的哈希表来保证避免冲突,它可以将一个随机值从哈希函数的域中映射到任意一个特定元素,并限定在1/k的范围内。(如果这让你更加的糊涂,千万别担心!)
我们将选择合适的哈希函数的方法成为冲突避免机制(collision avoidance),已有许多研究设计这一领域,因为哈希函数的选择直接影响了哈希表的整体性能。在下一节,我们会介绍在.Net Framework的Hashtable类中对哈希函数的使用。
有很多方法处理冲突问题。最直接的方法,我们称为“冲突解决机制”(collision resolution),是将要插入到哈希表中的对象放到另外一块空间中,因为实际的空间已经被占用了。其中一种最简单的方法称为“线性挖掘”(linear probing),实现步骤如下:
1. 当要插入一个新的元素时,用哈希函数在哈希表中定位;
2. 检查表中该位置是否已经存在元素,如果该位置内容为空,则插入并返回,否则转向步骤3。
3. 如果该地址为i,则检查i+1是否为空,如果已被占用,则检查i+2,依此类推,知道找到一个内容为空的位置。
例如:如果我们要将五个员工的信息插入到哈希表中:Alice(333-33-1234),Bob(444-44-1234), Cal (555-55-1237), Danny (000-00-1235), and Edward (111-00-1235)。当添加完信息后,如图十所示:

图十:有相似社保号的五位员工
Alice的社保号被“哈希(这里做动词用,译注)”为1234,因此存放位置为1234。接下来来,Bob的社保号也被“哈希”为1234,但由于位置1234处已经存在Alice的信息,所以Bob的信息就被放到下一个位置——1235。之后,添加Cal,哈希值为1237,1237位置为空,所以Cal就放到1237处。下一个是Danny,哈希值为1235。1235已被占用,则检查1236位置是否为空。既然为空,Danny就被放到那儿。最后,添加Edward的信息。同样他的哈希好为1235。1235已被占用,检查1236,也被占用了,再检查1237,直到检查到1238时,该位置为空,于是Edward被放到了1238位置。
搜索哈希表时,冲突仍然存在。例如,如上所示的哈希表,我们要访问Edward的信息。因此我们将Edward的社保号111-00-1235哈希为1235,并开始搜索。然而我们在1235位置找到的是Bob,而非Edward。所以我们再搜索1236,找到的却是Danny。我们的线性搜索继续查找知道找到Edward或找到内容为空的位置。结果我们可能会得出结果是社保号为111-00-1235的员工并不存在。
线性挖掘虽然简单,但并是解决冲突的好的策略,因为它会导致同类聚合(clustering)。如果我们要添加10个员工,他们的社保号后四位均为3344。那么有10个连续空间,从3344到3353均被占用。查找这10个员工中的任一员工都要搜索这一簇位置空间。而且,添加任何一个哈希值在3344到3353范围内的员工都将增加这一簇空间的长度。要快速查询,我们应该让数据均匀分布,而不是集中某几个地方形成一簇。
更好的挖掘技术是“二次挖掘”(quadratic probing),每次检查位置空间的步长以平方倍增加。也就是说,如果位置s被占用,则首先检查s+12处,然后检查s-12,s+22,s-22,s+32 依此类推,而不是象线性挖掘那样从s+1,s+2……线性增长。当然二次挖掘同样会导致同类聚合。
下一节我们将介绍第三种冲突解决机制——二度哈希,它被应用在.Net Framework的哈希表类中。
System.Collections.Hashtable 类
.Net Framework 基类库包括了Hashtable类的实现。当我们要添加元素到哈希表中时,我们不仅要提供元素(item),还要为该元素提供关键字(key)。Key和item可以是任意类型。在员工例子中,key为员工的社保号,item则通过Add()方法被添加到哈希表中。
要获得哈希表中的元素(item),你可以通过key作为索引访问,就象在数组中用序数作为索引那样。下面的C#小程序演示了这一概念。它以字符串值作为key添加了一些元素到哈希表中。并通过key访问特定的元素。
using System;
using System.Collections;
public class HashtableDemo
{
private static Hashtable ages = new Hashtable();
public static void Main()
{
// Add some values to the Hashtable, indexed by a string key
ages.Add("Scott", 25);
ages.Add("Sam", 6);
ages.Add("Jisun", 25);
// Access a particular key
if (ages.ContainsKey("Scott"))
{
int scottsAge = (int) ages["Scott"];
Console.WriteLine("Scott is " + scottsAge.ToString());
}
else
Console.WriteLine("Scott is not in the hash table...");
}
}
程序中的ContainsKey()方法,是根据特定的key判断是否存在符合条件的元素,返回布尔值。Hashtable类中包含keys属性(property),返回哈希表中使用的所有关键字的集合。这个属性可以通过遍历访问,如下:
// Step through all items in the Hashtable
foreach(string key in ages.Keys)
Console.WriteLine("Value at ages[/"" + key + "/"] = " + ages[key].ToString());
要认识到插入元素的顺序和关键字集合中key的顺序并不一定相同。关键字集合是以存储的关键字对应的元素为基础,上面的程序的运行结果是:
Value at ages["Jisun"] = 25
Value at ages["Scott"] = 25
Value at ages["Sam"] = 6
即使插入到哈希表中的顺序是:Scott,Sam, Jisun。
Hashtable类的哈希函数
Hashtable类中的哈希函数比我们前面介绍的社保号的哈希值更加复杂。首先,要记住的是哈希函数返回的值是序数。对于社保号的例子来说很容易办到,因为社保号本身就是数字。我们只需要截取其最后四位数,就可以得到合适的哈希值。然而Hashtable类中可以接受任何类型的值作为key。就象上面的例子,key是字符串类型,如“Scott”或“Sam”。在这样一个例子中,我们自然想明白哈希函数是怎样将string转换为数字的。
这种奇妙的转换应该归功于GetHashCode()方法,它定义在System.Object类中。Object类中GetHashCode()默认的实现是返回一个唯一的整数值以保证在object的生命期中不被修改。既然每种类型都是直接或间接从Object派生的,因此所以object都可以访问该方法。自然,字符串或其他类型都能以唯一的数字值来表示。
Hashtable类中的对于哈希函数的定义如下:
H(key) = [GetHash(key) + 1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1))] % hashsize
这里的GetHash(key),默认为对key调用GetHashCode()方法的返回值(虽然在使用Hashtable时,你可以自定义GetHash()函数)。GetHash(key)>>5表示将得到key的哈希值,向右移动5位,相当于将哈希值除以32。%操作符就是之前介绍的求模运算符。Hashsize指的是哈希表的长度。因为要进行求模,因此最后的结果H(k)在0到hashsize-1之间。既然hashsize为哈希表的长度,因此结果总是在可以接受的范围内。
Hashtable类中的冲突解决方案
当我们在哈希表中添加或获取一个元素时,会发生冲突。插入元素时,必须查找内容为空的位置,而获取元素时,即使不在预期的位置处,也必须找到该元素。前面我们简单地介绍了两种解决冲突的机制——线性和二次挖掘。在Hashtable类中使用的是一种完全不同的技术,成为二度哈希(rehasing)(有的资料也将其称为双精度哈希double hashing)。
二度哈希的工作原理如下:有一个包含多个哈希函数(H1……Hn)的集合。当我们要从哈希表中添加或获取元素时,首先使用哈希函数H1。如果导致冲突,则尝试使用H2,一直到Hn。各个哈希函数极其相似,不同的是它们选用的乘法因子。通常,哈希函数Hk的定义如下:
Hk(key) = [GetHash(key) + k * (1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1)))] % hashsize
注:运用二度哈希重要的是在执行了hashsize次挖掘后,哈希表中的每一个位置都确切地被有且仅有一次访问。也就是说,对于给定的key,对哈希表中的同一位置不会同时使用Hi和Hj。在Hashtable类中使用二度哈希公式,其保证为:(1 + (((GetHash(key) >> 5) + 1) % (hashsize – 1))与hashsize两者互为素数。(两数互为素数表示两者没有共同的质因子。)如果hashsize是一个素数,则保证这两个数互为素数。
二度哈希较前两种机制较好地避免了冲突。
调用因子(load factors)和扩充哈希表
Hashtable类中包含一个私有成员变量loadFactor,它指定了哈希表中元素个数与表位置总数之间的最大比例。例如:loadFactor等于0.5,则说明哈希表中只有一半的空间存放了元素值,其余一半皆为空。
哈希表的构造函数以重载的方式,允许用户指定loadFactor值,定义范围为0.1到1.0。要注意的是,不管你提供的值是多少,范围都不超过72%。即使你传递的值为1.0,Hashtable类的loadFactor值还是0.72。微软认为loadFactor的最佳值为0.72,因此虽然默认的loadFactor为1.0,但系统内部却自动地将其改变为0.72。所以,建议你使用缺省值1.0(事实上是0.72,有些迷惑,不是吗?)
注:我花了好几天时间去咨询微软的开发人员为什么要使用自动转换?我弄不明白,为什么他们不直接规定值为0.072到0.72之间。最后我从编写Hashtable类的开发团队的到了答案,他们非常将问题的缘由公诸于众。事实上,这个团队经过测试发现如果loadFactor超过了0.72,将会严重的影响哈希表的性能。他们希望开发人员能够更好地使用哈希表,但却可能记不住0.72这个无规律数,相反如果规定1.0为最佳值,开发者会更容易记住。于是,就形成现在的结果,虽然在功能上有少许牺牲,但却使我们能更加方便地使用数据结构,而不用感到头疼。
向Hashtable类添加新元素时,都要进行检查以保证元素与空间大小的比例不会超过最大比例。如果超过了,哈希表空间将被扩充。步骤如下:
1. 哈希表的位置空间近似地成倍增加。准确地说,位置空间值从当前的素数值增加到下一个最大的素数值。(回想一下前面讲到的二度哈希的工作原理,哈希表的位置空间值必须是素数。)
2. 既然二度哈希时,哈希表中的所有元素值将依赖于哈希表的位置空间值,所以表中所有值也需要二度哈希(因为在第一步中位置空间值增加了)。
幸运的是,Hashtable类中的Add()方法隐藏了这些复杂的步骤,你不需要关心它的实现细节。
调用因子(load factor)对冲突的影响决定于哈希表的总体长度和进行挖掘操作的次数。Load factor越大,哈希表越密集,空间就越少,比较于相对稀疏的哈希表,进行挖掘操作的次数就越多。如果不作精确地分析,当冲突发生时挖掘操作的预期次数大约为1/(1-lf),这里lf指的是load factor。
如前所述,微软将哈希表的缺省调用因子设定为0.72。因此对于每次冲突,平均挖掘次数为3.5次。既然该数字与哈希表中实际元素个数无关,因此哈希表的渐进访问时间为O(1),显然远远好于数组的O(n)。
最后,我们要认识到对哈希表的扩充将以性能损耗为代价。因此,你应该预先估计你的哈希表中最后可能会容纳的元素总数,在初始化哈希表时以合适的值进行构造,以避免不必要的扩充。

先到此为止,好好享受编程的乐趣吧!
Scott Mitchell
4GuysFromRolla.com
February 9, 2004
Summary: This article, the fourth in the series, begins with a quick examination of AVL trees and red-black trees, which are two different self-balancing, binary search tree data structures. The remainder of the article examines the skip list data structure, an ingenious data structure that turns a linked list into a data structure that offers the same running time as the more complex self-balancing tree data structures. (31 printed pages)
Note This article assumes the reader is familiar with C# and the data structure topics discussed previously in this article series.
Download the BuildingBetterBST.msi sample file.
Contents
Introduction
Self-Balancing Binary Search Trees
A Quick Primer on Linked Lists
Skip Lists: A Linked List with Self-Balancing BST-Like Properties
Conclusion
Books
Introduction
In Part 3 of this article series, we looked at the general tree data structure. A tree is a data structure that consists of nodes, where each node has some value and an arbitrary number of children nodes. Trees are common data structures because many real-world problems exhibit tree-like behavior. For example, any sort of hierarchical relationship among people, things, or objects can be modeled as a tree.
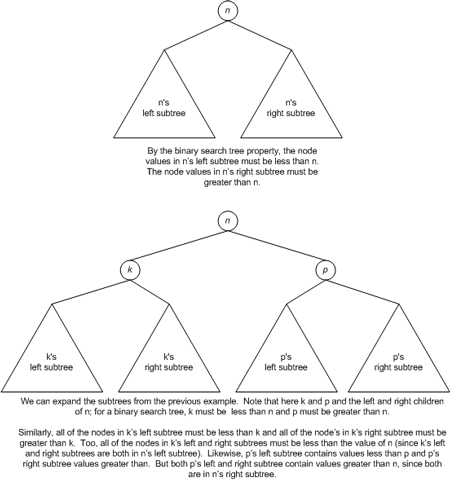
A binary tree is a special kind of tree, which limits each node to no more than two children. A binary search tree, or BST, is a binary tree whose nodes are arranged such that for every node n, all of the nodes in n's left subtree have a value less than n, and all nodes in n's right subtree have a value greater than n. As we discussed, in the average case BSTs offer log2 n asymptotic time for inserts, deletes, and searches. (log2 n is often referred to as sublinear because it outperforms linear asymptotic times.)
The disadvantage of BSTs is that in the worst-case their asymptotic running time is reduced to linear time. This happens if the items inserted into the BST are inserted in order or in near-order. In such a case, a BST performs no better than an array. As we discussed at the end of Part 3, there exist self-balancing binary search trees that ensure that regardless of the order of the data inserted, the tree maintains a log2 n running time. In this article, we'll briefly discuss two self-balancing binary search trees—AVL trees and red-black trees. Following that, we'll take an in-depth look at skip lists. Skip lists are a really cool data structure that is much easier to implement than AVL trees or red-black trees, yet still guarantees a running time of log2 n.
Self-Balancing Binary Search Trees
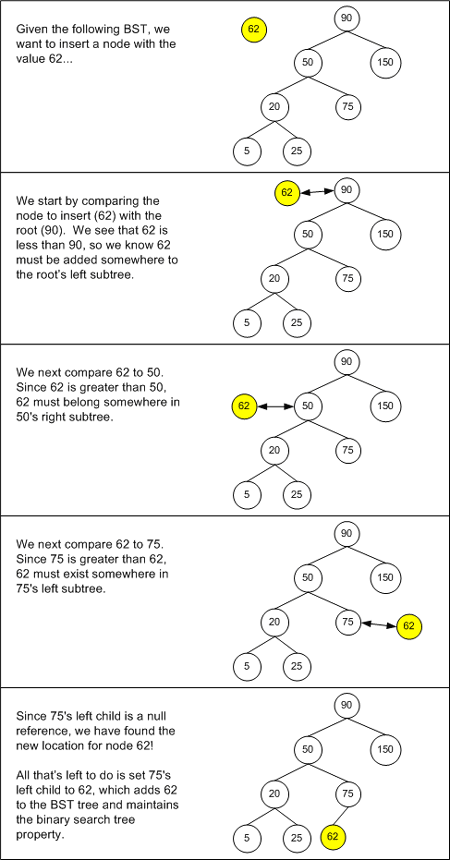
Recall that new nodes are inserted into a binary search tree at the leaves. That is, adding a node to a binary search tree involves tracing down a path of the binary search tree, taking lefts and rights based on the comparison of the value of the current node, and the node being inserted, until the path reaches a dead end. At this point, the newly inserted node is plugged into the tree at this reached dead end. Figure 1 illustrates the process of inserting a new node into a BST.

Figure 1. Inserting a new node into a BST
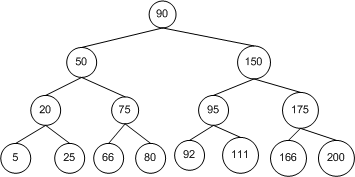
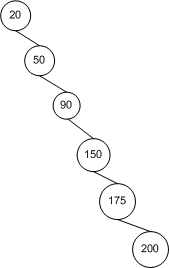
As Figure 1 shows, when making the comparison at the current node, the node to be inserted travels down the left path if its value is less than the current node, and down the right if its value is greater than the current node's value. Therefore, the structure of the BST is relative to the order with which the nodes are inserted. Figure 2 depicts a BST after nodes with values of 20, 50, 90, 150, 175, and 200 have been added. Specifically, these nodes have been added in ascending order. The result is a BST with no breadth. That is, its topology consists of a single line of nodes rather than having the nodes fanned out.

Figure 2. A BST after nodes with values of 20, 50, 90, 150, 175, and 200 have been added
BSTs—which offer sublinear running time for insertions, deletions, and searches—perform optimally when their nodes are arranged in a fanned-out manner. This is because when searching for a node in a BST, each single step down the tree reduces the number of nodes that need to be potentially checked by one half. However, when a BST has a topology similar to the one in Figure 2, the running time for the BST's operations are much closer to linear time. To see why, consider what must happen when searching for a particular value, such as 175. Starting at the root, 20, we must navigate down through each right child until we hit 175. That is, there is no savings in nodes that need to be checked at each step. Searching a BST like the one in Figure 2 is identical to searching an array. Each element must be checked one at a time. Therefore, such a structured BST exhibits a linear search time.
What is important to realize is that the running time of a BST's operations is related to the BST's height. The height of a tree is defined as the length of the longest path starting at the root. The height of a tree can be defined recursively as follows:
- The height of a node with no children is 0
- The height of a node with one child is the height of that child plus one
- The height of a node with two children is one plus the greater height of the two children
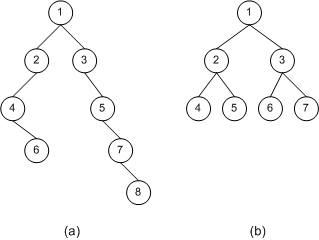
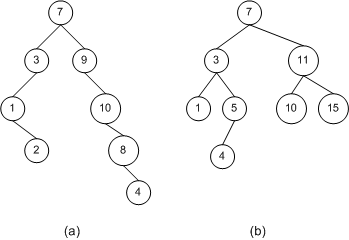
To compute the height of a tree, start at its leaf nodes and assign them a height of 0. Then move up the tree using the three rules outlined to compute the height of each leaf nodes' parent. Continue in this manner until every node of the tree has been labeled. The height of the tree, then, is the height of the root node. Figure 3 shows a number of binary trees with their height computed at each node. For practice, take a second to compute the heights of the trees yourself to make sure your numbers match up with the numbers presented in the figure below.

Figure 3. Example binary trees with their height computed at each node
A BST exhibits log2 n running times when its height, when defined in terms of the number of nodes, n, in the tree, is near the floor of log2 n. (The floor of a number x is the greatest integer less than x. So the floor of 5.38 would be 5; the floor of 3.14159 would be 3. For positive numbers x, the floor of x can be found by simply truncating the decimal part of x, if any.) Of the three trees in Figure 3, tree (b) has the best height to number of nodes ratio, as the height is 3 and the number of nodes present in the tree is 8. As we discussed in Part 1 of this article series, loga b = y is another way of writing ay = b. log2 8, then, equals 3 since 23 = 8. Tree (a) has 10 nodes and a height of 4. log2 10 equals 3.3219 and change, the floor of that being 3. So, 4 is not the ideal height. Notice that by rearranging the topology of tree (a)—by moving the far-bottom right node to the child of one of the non-leaf nodes with only one child—we could reduce the tree's height by one, thereby giving the tree an optimal height to node ratio. Finally, tree (c) has the worst height to node ratio. With its 5 nodes it could have an optimal height of 2, but due to its linear topology is has a height of 4.
The challenge we are faced with, then, is ensuring that the topology of the resulting BST exhibits an optimal ratio of height to the number of nodes. Since the topology of a BST is based upon the order with which the nodes are inserted, intuitively you might opt to solve this problem by ensuring that the data that's added to a BST is not added in near-sorted order. While this is possible if you know the data that will be added to the BST beforehand, it might not be practical. If you are not aware of the data that will be added—like if it's added based on user input, or added as it's read from a sensor—then there is no hope of guaranteeing the data is not inserted in near-sorted order. The solution, then, is not to try to dictate the order with which the data is inserted, but to ensure that after each insertion the BST remains balanced. Data structures that are designed to maintain balance are referred to as self-balancing binary search trees.
A balanced tree is a tree that maintains some predefined ratio between its height and breadth. Different data structures define their own ratios for balance, but all have it close to log2 n. A self-balancing BST, then, exhibits log2 n running time. There are numerous self-balancing BST data structures in existence, such as AVL trees, red-black trees, 2-3 trees, 2-3-4 trees, splay trees, B-trees, and others. In the next two sections, we'll take a brief look at two of these self-balancing trees—AVL trees and red-black trees.
Examining AVL Trees
In 1962 Russian mathematicians G. M. Andel'son-Vel-skii and E. M. Landis invented the first self-balancing BST, called an AVL tree. AVL trees must maintain the following balance property: for every node n, the height of n's left and right subtrees can differ by at most 1. The height of a node's left or right subtree is the height computed for its left or right node using the technique discussed in the previous section. If a node has only one child, say a left child, but no right child, then the height of the right subtree is -1.
Figure 4 shows, conceptually, the height-relationship each node in an AVL tree must maintain. Figure 5 provides three examples of BSTs. The numbers in the nodes represent the nodes' values; the numbers to the right and left of each node represent the height of the nodes' left and right subtrees. In Figure 5, trees (a) and (b) are valid AVL trees, but trees (c) and (d) are not because not all nodes adhere to the AVL balance property.

Figure 4. The height of left and right subtrees in an AVL tree cannot differ by more than one.
Figure 5. Example trees, where (a) and (b) are valid AVL trees, but (c) and d are not.
Note Realize that AVL trees are binary search trees, so in addition to maintaining a balance property, an AVL tree must also maintain the binary search tree property.
When creating an AVL tree data structure, the challenge is to ensure that the AVL balance remains regardless of the operations performed on the tree. That is, as nodes are added or deleted, it is vital that the balance property remains. AVL trees maintain the balance through rotations. A rotation slightly reshapes the tree's topology such that the AVL balance property is restored and, equally important, the binary search tree property is maintained as well.
Inserting a new node into an AVL tree is a two-stage process. First, the node is inserted into the tree using the same algorithm for adding a new node to a BST. That is, the new node is added as a leaf node in the appropriate location to maintain the BST property. After adding a new node, it might be the case that adding this new node caused the AVL balance property to be violated at some node along the path traveled down from the root to where the newly inserted node was added. To fix any violations, stage two involves traversing back up the access path, checking the height of the left and right subtree for each node along this return path. If the heights of the subtrees differ by more than 1, a rotation is performed to fix the anomaly.
Figure 6 illustrates the steps for a rotation on node 3. Notice that after stage 1 of the insertion routine, the AVL tree property was violated at node 5 because node 5's left subtree's height was two greater than its right subtree's height. To remedy this violation, a rotation was performed on node 3, the root of node 5's left subtree. This rotation fixed the balance inconsistency and also maintained the BST property.

Figure 6. AVL trees stay balanced through rotations
In addition to the simple, single rotation shown in Figure 6, there are more involved rotations that are sometimes required. A thorough discussion of the set of rotations potentially needed by an AVL tree is beyond the scope of this article. What is important to realize is that both insertions and deletions can disturb the balance property or which AVL trees must adhere. To fix any perturbations, rotations are used.
Note To familiarize yourself with insertions, deletions, and rotations from an AVL tree, check out the AVL tree applet at http://www.seanet.com/users/arsen/avltree.html. This Java applet illustrates how the topology of an AVL tree changes with additions and deletions.
By ensuring that all nodes' subtrees' heights differ by at most 1, AVL trees guarantee that insertions, deletions, and searches will always have an asymptotic running time of log2 n, regardless of the order of insertions into the tree.
A Look at Red-Black Trees
Rudolf Bayer, a computer science professor at the Technical University of Munich, invented the red-black tree data structure in 1972. In addition to its data and left and right children, the nodes of a red-black tree contain an extra bit of information—a color, which can be either red or black. Red-black trees are complicated further by the concept of a specialized class of node referred to as NIL nodes. NIL nodes are pseudo-nodes that exist as the leaves of the red-black tree. That is, all regular nodes—those with some data associated with them—are internal nodes. Rather than having a NULL pointer for a childless regular node, the node is assumed to have a NIL node in place of that NULL value. This concept can be understandably confusing, and hopefully the diagram in Figure 7 clears up any confusion.

Figure 7. Red-black trees add the concept of a NIL node.
Red-black trees are trees that have the following four properties:
- Every node is colored either red or black.
- Every NIL node is black.
- If a node is red, then both of its children are black.
- Every path from a node to a descendant leaf contains the same number of black nodes.
The first three properties are self-explanatory. The fourth property, which is the most important of the four, simply states that starting from any node in the tree, the number of black nodes from that node to any leaf (NIL), must be the same. In Figure 7 take the root node as an example. Starting from 41 and going to any NIL, you encounter the same number of black nodes—3. For example, taking a path from 41 to the left-most NIL node, we start on 41, a black node. We then travel down to node 9, then node 2, which is also black, then node 1, and finally the left-most NIL node. In this journey we encountered three black nodes—41, 2, and the final NIL node. In fact, if we travel from 41 to any NIL node, we'll always encounter precisely three black nodes.
Like the AVL tree, red-black trees are another form of self-balancing binary search tree. Whereas the balance property of an AVL tree was explicitly stated as a relationship between the heights of each node's left and right subtrees, red-black trees guarantee their balance in a more conspicuous manner. It can be shown that a tree that implements the four red-black tree properties has a height that is always less than 2 * log2 (n+1), where n is the total number of nodes in the tree. For this reason, red-black trees ensure that all operations can be performed within an asymptotic running time of log2 n.
Like AVL trees, any time a red-black tree has nodes inserted or deleted, it is important to verify that the red-black tree properties have not been violated. With AVL trees, the balance property was restored through rotations. With red-black trees, the red-black tree properties are restored through re-coloring and rotations. Red-black trees are notoriously complex in their re-coloring and rotation rules, requiring the nodes along the access path to make decisions based upon their color in contrast to the color of their parents and uncles. (An uncle of a node n is the node that is n's parent's sibling node.) A thorough discussion of re-coloring and rotation rules is far beyond the scope of this article.
To view the re-coloring and rotations of a red-black tree as nodes are added and deleted, check out the red-black tree applet, which can also be accessed viewed at http://www.seanet.com/users/arsen/avltree.html.
A Quick Primer on Linked Lists
One common data structure we've yet to discuss is the linked list. Since the skip list data structure we'll be examining next is the mutation of a linked list into a data structure with self-balanced binary tree running times, it is important that before diving into the specifics of skip lists we take a moment to discuss linked lists.
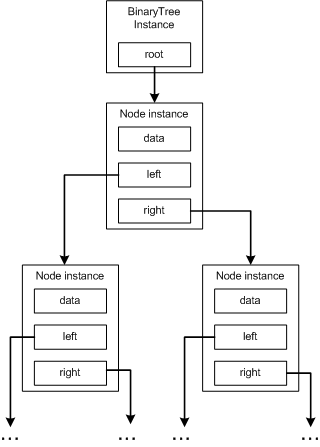
Recall that with a binary tree, each node in the tree contains some bit of data and a reference to its left and right children. A linked list can be thought of as a unary tree. That is, each element in a linked list has some data associated with it, and a single reference to its neighbor. As Figure 8 illustrates, each element in a linked list forms a link in the chain. Each link is tied to its neighboring node, which is the node on its right.

Figure 8. A four-element linked list
When we created a binary tree data structure in Part 3, the binary tree data structure only needed to contain a reference to the root of the tree. The root itself contained references to its children, and those children contained references to their children, and so on. Similarly, with the linked list data structure, when implementing a structure we only need to keep a reference to the head of the list since each element in the list maintains a reference to the next item in the list.
Linked lists have the same linear running time for searches as arrays. That is, to determine if the element Sam is in the linked list in Figure 8, we have to start at the head and check each element one by one. There are no shortcuts as with binary trees or hashtables. Similarly, deleting from a linked list takes linear time because the linked list must first be searched for the item to be deleted. Once the item is found, removing it from the linked list involves reassigning the deleted item's left neighbor's neighbor reference to the deleted item's neighbor. Figure 9 illustrates the pointer reassignment that must occur when deleting an item from a linked list.

Figure 9. Deleting an element from a linked list
The asymptotic time required to insert a new element into a linked list depends on whether or not the linked list is a sorted list. If the list's elements need not be sorted, insertion can occur in constant time because we can add the element to the front of the list. This involves creating a new element, having its neighbor reference point to the current linked list head, and, finally, reassigning the linked list's head to the newly inserted element.
If the linked list elements need to be maintained in sorted order, then when adding a new element the first step is to locate where it belongs in the list. This is accomplished by exhaustively iterating from the beginning of the list to the element until the spot where the new element belongs. Let e be the element immediately before the location where the new element will be added. To insert the new element, e's processor reference must now point to the newly inserted element, and the new element's neighbor reference needs to be assigned to e's old neighbor. Figure 10 illustrates this concept graphically.

Figure 10. Inserting elements into a sorted linked list
Notice that linked lists do not provide direct access, like an array. That is, if you want to access the ith element of a linked list, you have to start at the front of the list and walk through i links. With an array, though, you can jump straight to the ith element. Given this, along with the fact that linked lists do not offer better search running times than arrays, you might wonder why anyone would want to use a linked list.
The primary benefit of linked lists is that adding or removing items does not involve messy and time-consuming re-dimensioning. Recall that array's have fixed size. If an array needs to have more elements added to it than it has capacity, the array must be re-dimensioned. Granted, the ArrayList class hides the code complexity of this, but re-dimensioning still carries with it a performance penalty. In short, an array is usually a better choice if you have an idea on the upper bound of the amount of data that needs to be stored. If you have no conceivable notion as to how many elements need to be stored, then a link list might be a better choice.
In summary, linked lists are fairly simple to implement. The main challenge comes with the threading or rethreading of the neighbor links with insertions or deletions, but the complexity of adding or removing an element from a linked list pales in comparison to the complexity of balancing an AVL or red-black tree.
Skip Lists: A Linked List with Self-Balancing BST-Like Properties
Back in 1989 William Pugh, a computer science professor at the University of Maryland, was looking at sorted linked lists one day thinking about their running time. Clearly a sorted linked list takes linear time to search because each element may potentially be visited, one right after the other. Pugh thought to himself that if half the elements in a sorted linked list had two neighbor references—one pointing to its immediate neighbor, and another pointing to the neighbor two elements ahead—while the other half had one, then searching a sorted linked list could be done in half the time. Figure 11 illustrates a two-reference sorted linked list.

Figure 11. A skip list
The way such a linked list saves search time is due in part to the fact that the elements are sorted, as well as the varying heights. To search for, say, Dave, we'd start at the head element, which is a dummy element whose height is the same height as the maximum element height in the list. The head element does not contain any data. It merely serves as a place to start searching.
We start at the highest link because it lets us skip over lower elements. We begin by following the head element's top link to Bob. At this point we can ask ourselves, does Bob come before or after Dave? If it comes before Dave, then we know Dave, if he's in the list, must exist somewhere to the right of Bob. If Bob comes before Dave, then Bob must exist somewhere between where we're currently positioned and Bob. In this case, Dave comes after Bob alphabetically, so we can repeat our search again from the Bob element. Notice that by moving onto Bob, we are skipping over Alice. At Bob, we repeat the search at the same level. Following the top-most pointer we reach Dave. Since we have found what we are looking for, we can stop searching.
Now, imagine that we wanted to search for Cal. We'd begin by starting at the head element, and then moving onto Bob. At Bob, we'd start by following the top-most reference to Dave. Since Dave comes after Cal, we know that Cal must exist somewhere between Bob and Dave. Therefore, we move down to the next lower reference level and continue our comparison.
The efficiency of such a linked list arises because we are able to move two elements over every time instead of just one. This makes the running time on the order of n/2, which, while better than a regular sorted link list, is still an asymptotically linear running time. Realizing this, Pugh wondered what would happen if rather than limiting the height of an element to 2, it was instead allowed to go up to log2 n for n elements. That is, if there were 8 elements in the linked list, there would be elements with height up to 3. If there were 16 elements, there would be elements with height up to 4. As Figure 12 shows, by intelligently choosing the heights of each of the elements, the search time is reduced to log2 n.

Figure 12. By increasing the height of each node in a skip list, better searching performance can be gained.
Notice that in the nodes in Figure 12, every 2ith node has references 2i elements ahead (that is, the 20 element). Alice has a reference to 20 elements ahead—Bob. The 21 element, Bob, has a reference to a node 21 elements ahead—Dave. Dave, the 22 element, has a reference 22 elements ahead—Frank. Had there been more elements, Frank—the 23 element—would have a reference to the element 23 elements ahead.
The disadvantage of the approach illustrated in Figure 12 is that adding new elements or removing existing ones can wreak havoc on the precise structure. That is, if Dave is deleted, now Ed becomes the 22 element, and Gil the 23 element, and so on. This means all of the elements to the right of the deleted element need to have their height and references readjusted. The same problem crops up with inserts. This redistribution of heights and references would not only complicate the code for this data structure, but would also reduce the insertion and deletion running times to linear.
Pugh noticed that this pattern created 50 percent of the elements at height 1, 25 percent at height 2, 12.5 percent at height 3, and so on. That is, 1/2i percent of the elements were at height i. Rather than trying to ensure the correct heights for each element with respect to its ordinal index in the list, Pugh decided to randomly pick a height using the ideal distribution—50 percent at height 1, 25 percent at height 2, and so on. What Pugh discovered was that such a randomized linked list was not only very easy to create in code, but that it also exhibited log2 n running time for insertions, deletions, and lookups. Pugh named his randomized lists skip lists because iterating through the list skips over lower-height elements.
In the remaining sections we'll examine the insertion, deletion, and lookup functions of the skip list, and implement them in a C# class. We'll finish off with an empirical look at the skip list performance and discuss the tradeoffs between skip lists and self-balancing BSTs.
Creating the Node and NodeList Classes
A skip list, like a binary tree, is made up of a collection of elements. Each element in a skip list has some data associated with it—a height, and a collection of element references. For example, in Figure 12 the Bob element has the data Bob, a height of 2, and two element references, one to Dave and one to Cal. Before creating a skip list class, we first need to create a class that represents an element in the skip list. I named this class Node, and its germane code is shown below. (The complete skip list code is available in this article as a code download.)
public class Node
{
#region Private Member Variables
private NodeList nodes;
IComparable myValue;
#endregion
#region Constructors
public Node(IComparable value, int height)
{
this.myValue = value;
this.nodes = new NodeList(height);
}
#endregion
#region Public Properties
public int Height
{
get { return nodes.Capacity; }
}
public IComparable Value
{
get { return myValue; }
}
public Node this[int index]
{
get { return nodes[index]; }
set { nodes[index] = value; }
}
#endregion
}
Notice that the Node class only accepts objects that implement the IComparable interface as data. This is because a skip list is maintained as a sorted list, meaning that its elements are ordered by their data. In order to order the elements, the data of the elements must be comparable. (If you remember back to Part 3, our binary search tree Node class also required that its data implement IComparable for the same reason.)
The Node class uses a NodeList class to store its collection of Node references. The NodeList class, shown below, is a strongly-typed collection of Nodes and is derived from System.Collections.CollectionBase.
public class NodeList : CollectionBase
{
public NodeList(int height)
{
// set the capacity based on the height
base.InnerList.Capacity = height;
// create dummy values up to the Capacity
for (int i = 0; i < height; i++)
base.InnerList.Add(null);
}
// Adds a new Node to the end of the node list
public void Add(Node n)
{
base.InnerList.Add(n);
}
// Accesses a particular Node reference in the list
public Node this[int index]
{
get { return (Node) base.InnerList[index]; }
set { base.InnerList[index] = value; }
}
// Returns the capacity of the list
public int Capacity
{
get { return base.InnerList.Capacity; }
}
}
The NodeList constructor accepts a height input parameter that indicates the number of references that the node needs. It appropriately sets the Capacity of the InnerList to this height and adds null references for each of the height references.
With the Node and NodeList classes created, we're ready to move on to creating the SkipList class. The SkipList class, as we'll see, contains a single reference to the head element. It also provides methods for searching the list, enumerating through the list's elements, adding elements to the list, and removing elements from the list.
Note For a graphical view of skip lists in action, be sure to check out the skip list applet at http://iamwww.unibe.ch/~wenger/DA/SkipList/. You can add and remove items from a skip list and visually see how the structure and height of the skip list is altered with each operation.
Creating the SkipList Class
The SkipList class provides an abstraction of a skip list. It contains public methods like:
- Add(IComparable): adds a new item to the skip list.
- Remove(IComparable): removes an existing item from the skip list.
- Contains(IComparable): returns true if the item exists in the skip list, false otherwise.
And public properties, such as:
- Height: the height of the tallest element in the skip list.
- Count: the total number of elements in the skip list.
The skeletal structure of the class is shown below. Over the next several sections, we'll examine the skip list's operations and fill in the code for its methods.
public class SkipList
{
#region Private Member Variables
Node head;
int count;
Random rndNum;
protected const double PROB = 0.5;
#endregion
#region Public Properties
public virtual int Height
{
get { return head.Height; }
}
public virtual int Count
{
get { return count; }
}
#endregion
#region Constructors
public SkipList() : this(-1) {}
public SkipList(int randomSeed)
{
head = new Node(1);
count = 0;
if (randomSeed < 0)
rndNum = new Random();
else
rndNum = new Random(randomSeed);
}
#endregion
protected virtual int chooseRandomHeight(int maxLevel)
{
...
}
public virtual bool Contains(IComparable value)
{
...
}
public virtual void Add(IComparable value)
{
...
}
public virtual void Remove(IComparable value)
{
...
}
}
We'll fill in the code for the methods in a bit, but for now pay close attention to the class's private member variables, public properties, and constructors. There are three relevant private member variables:
- head, which is the list's head element. Remember that a skip list has a dummy head element (refer back to Figures 11 and 12 for a graphical depiction of the head element).
- count, an integer value keeping track of how many elements are in the skip list.
- rndNum, an instance of the Random class. Since we need to randomly determine the height when adding a new element to the list, we'll use this Random instance to generate the random numbers.
The SkipList class has two read-only public properties, Height and Count. Height returns the height of the tallest skip list element. Since the head is always equal to the tallest skip list element, we can simply return the head element's Height property. The Count property simply returns the current value of the private member variable count. (count, as we'll see, is incremented in the Add() method and decremented in the Remove() method.)
Notice there are two forms of the SkipList constructor. The default constructor merely calls the second, passing in a value of -1. The second form assigns to head a new Node instance with height 1, and sets count equal to 0. It then checks to see if the passed in randomSeed value is less than 0 or not. If it is, then it creates an instance of the Random class using an auto-generated random seed value. Otherwise, it uses the random seed value passed into the constructor.
Note Computer random-number generators, such as the Random class in the .NET Framework, are referred to as pseudo-random number generators because they don't pick random numbers, but instead use a function to generate the random numbers. The random number generating function works by starting with some value, called the seed. Based on the seed, a sequence of random numbers are computed. Slight changes in the seed value lead to seemingly random changes in the series of numbers returned.
If you use the Random class's default constructor, the system clock is used to generate a seed. You can optionally specify a seed. The benefit of specifying a seed is that if you use the same seed value, you'll get the same sequence of random numbers. Being able to get the same results is beneficial when testing the correctness and efficiency of a randomized algorithm like the skip list.
Searching a skip list
The algorithm for searching a skip list for a particular value is straightforward. Non-formally, the search process can be described as follows: we start with the head element's top-most reference. Let e be the element referenced by the head's top-most reference. We check to see if the e's value is less than, greater than, or equal to the value for which we are searching. If it equals the value, then we have found the item for which we're looking. If it's greater than the value we're looking for and if the value exists in the list, it must be to the left of e, meaning it must have a lesser height than e. Therefore, we move down to the second level head node reference and repeat this process.
If, on the other hand, the value of e is less than the value we're looking for then the value, if it exists in the list, must be on the right hand side of e. Therefore, we repeat these steps for the top-most reference of e. This process continues until we find the value we're searching for, or exhaust all the "levels" without finding the value.
More formally, the algorithm can be spelled out with the following pseudo-code:
Node current = head
for i = skipList.Height downto 1
while current[i].Value < valueSearchingFor
current = current[i] // move to the next node
if current[i].Value == valueSearchingFor then
return true
else
return false
Take a moment to trace the algorithm over the skip list shown in Figure 13. The red arrows show the path of checks when searching the skip lists. Skip list (a) shows the results when searching for Ed. Skip list (b) shows the results when searching for Cal. Skip list (c) shows the results when searching for Gus, which does not exist in the skip list. Notice that throughout the algorithm we are moving in a right, downward direction. The algorithm never moves to a node to the left of the current node, and never moves to a higher reference level.

Figure 13. Searching over a skip list.
The code for the Contains(IComparable) method is quite simple, involving a while and a for loop. The for loop iterates down through the reference level layers. The while loop iterates across the skip list's elements.
public virtual bool Contains(IComparable value)
{
Node current = head;
int i = 0;
for (i = head.Height - 1; i >= 0; i--)
{
while (current[i] != null)
{
int results = current[i].Value.CompareTo(value);
if (results == 0)
return true;
else if (results < 0)
current = current[i];
else // results > 0
break; // exit while loop
}
}
// if we reach here, we searched to the end of the list without finding the element
return false;
}
Inserting into a skip list
Inserting a new element into a skip list is akin to adding a new element in a sorted link list, and involves two steps:
- Locate where in the skip list the new element belongs. This location is found by using the search algorithm to find the location that comes immediately before the spot the new element will be added
- Thread the new element into the list by updating the necessary references.
Since skip list elements can have many levels and, therefore, many references, threading a new element into a skip list is not as simple as threading a new element into a simple linked list. Figure 14 shows a diagram of a skip list and the threading process that needs to be done to add the element Gus. For this example, imagine that the randomly determined height for the Gus element was 3. To successfully thread in the Gus element, we'd need to update Frank's level 3 and 2 references, as well as Gil's level 1 reference. Gus's level 1 reference would point to Hank. If there were additional nodes to the right of Hank, Gus's level 2 reference would point to the first element to the right of Hank with height 2 or greater, while Gus's level 3 reference would point to the first element right of Hank with height 3 or greater.

Figure 14. Inserting elements into a skip list
In order to properly rethread the skip list after inserting the new element, we need to keep track of the last element encountered for each height. In Figure 14, Frank was the last element encountered for references at levels 4, 3, and 2, while Gil was the last element encountered for reference level 1. In the insert algorithm below, this record of last elements for each level is maintained by the updates array, which is populated as the search for the location for the new element is performed.
public virtual void Add(IComparable value)
{
Node [] updates = new Node[head.Height];
Node current = head;
int i = 0;
// first, determine the nodes that need to be updated at each level
for (i = head.Height - 1; i >= 0; i--)
{
while (current[i] != null && current[i].Value.CompareTo(value) < 0)
current = current[i];
updates[i] = current;
}
// see if a duplicate is being inserted
if (current[0] != null && current[0].Value.CompareTo(value) == 0)
// cannot enter a duplicate, handle this case by either just returning or by throwing an exception
return;
// create a new node
Node n = new Node(value, chooseRandomHeight(head.Height + 1));
count++; // increment the count of elements in the skip list
// if the node's level is greater than the head's level, increase the head's level
if (n.Height > head.Height)
{
head.IncrementHeight();
head[head.Height - 1] = n;
}
// splice the new node into the list
for (i = 0; i < n.Height; i++)
{
if (i < updates.Length)
{
n[i] = updates[i][i];
updates[i][i] = n;
}
}
}
There are a couple of key portions of the Add(IComparable) method that are important. First, be certain to examine the first for loop. In this loop, not only is the correct location for the new element located, but the updates array is also fully populated. After this loop, a check is done to make sure that the data being entered is not a duplicate. I chose to implement my skip list such that duplicates are not allowed. However, skip lists can handle duplicate values just fine. If you want to allow for duplicates, simply remove this check.
Next, a new Node instance, n, is created. This represents the element to be added to the skip list. Note that the height of the newly created Node is determined by a call to the chooseRandomHeight() method, passing in the current skip list height plus one. We'll examine this method shortly. Another thing to note is that after adding the Node, a check is made to see if the new Node's height is greater than that of the skip list's head element's height. If it is, then the head element's height needs to be incremented, because the head element height should have the same height as the tallest element in the skip list.
The final for loop rethreads the references. It does this by iterating through the updates array, having the newly inserted Node's references point to the Nodes previously pointed to by the Node in the updates array, and then having the updates array Node update its reference to the newly inserted Node. To help clarify things, try running through the Add(IComparable) method code using the skip list in Figure 14, where the added Node's height is 3.
Randomly Determining the Newly Inserted Node's Height
When inserting a new element into the skip list, we need to randomly select a height for the newly added Node. Recall from our earlier discussions of skip lists that when Pugh first envisioned multi-level, linked-list elements, he imagined a linked list where each 2ith element had a reference to an element 2i elements away. In such a list, precisely 50 percent of the nodes would have height 1, 25 percent with height 2, and so on.
The chooseRandomHeight() method uses a simple technique to compute heights so that the distribution of values matches Pugh's initial vision. This distribution can be achieved by flipping a coin and setting the height to one greater than however many heads in a row were achieved. That is, if upon the first flip you get a tails, then the height of the new element will be one. If you get one heads and then a tails, the height will be 2. Two heads followed by a tails indicates a height of three, and so on. Since there is a 50 percent probability that you will get a tails, a 25 percent probability that you will get a heads and then a tails, a 12.5 percent probability that you will get two heads and then a tails, and so on. The distribution works out to be the same as the desired distribution.
The code to compute the random height is given by the following simple code snippet:
const double PROB = 0.5;
protected virtual int chooseRandomHeight()
{
int level = 1;
while (rndNum.NextDouble() < PROB)
level++;
return level;
}
One concern with the chooseRandomHeight()method is that the value returned might be extraordinarily large. That is, imagine that we have a skip list with, say, two elements, both with height 1. When adding our third element, we randomly choose the height to be 10. This is an unlikely event, since there is only roughly a 0.1 percent chance of selecting such a height, but it could conceivable happen. The downside of this, now, is that our skip list has an element with height 10, meaning there is a number of superfluous levels in our skip list. To put it more bluntly, the references at levels 2 up to 10 would not be utilized. Even as additional elements were added to the list, there's still only a 3 percent chance of getting a node over a height of 5, so we'd likely have many wasted levels.
Pugh suggests a couple of solutions to this problem. One is to simply ignore it. Having superfluous levels doesn't require any change in the code of the data structure, nor does it affect the asymptotic running time. The approach I chose to use is to use "fixed dice" when choosing the random level. That is, you restrict the height of the new element to be a height of at most one greater than the tallest element currently in the skip list. The actual implementation of the chooseRandomHeight() method is shown below, which implements this "fixed dice" approach. Notice that a maxLevel input parameter is passed in, and the while loop exits prematurely if level reaches this maximum. In the Add(IComparable) method, note that the maxLevel value passed in is the height of the head element plus one. (Recall that the head element's height is the same as the height of the maximum element in the skip list.)
protected virtual int chooseRandomHeight(int maxLevel)
{
int level = 1;
while (rndNum.NextDouble() < PROB && level < maxLevel)
level++;
return level;
}
The head element should be the same height as the tallest element in the skip list. So, in the Add(IComparable) method, if the newly added Node's height is greater than the head element's height, I call the IncrementHeight() method:
/* - snippet from the Add() method… */
if (n.Height > head.Height)
{
head.IncrementHeight();
head[head.Height - 1] = n;
}
/************************************/
The IncrementHeight() is a method of the Node class that I left out for brevity. It simply increases the Capacity of the Node's NodeList and adds a null reference to the newly added level. For the method's source code refer to the article's code sample.
Note In his paper, "Skip Lists: A Probabilistic Alternative to Balanced Trees," Pugh examines the effects of changing the value of PROB from 0.5 to other values, such as 0.25, 0.125, and others. Lower values of PROB decrease the average number of references per element, but increase the likelihood of the search taking substantially longer than expected. For more details, be sure to read Pugh's paper, which is mentioned in the References section at the end of this article.
Deleting an element from a skip list
Like adding an element to a skip list, removing an element involves a two-step process:
- The element to be deleted must be found.
- That element needs to be snipped from the list and the references need to be rethreaded.
Figure 15 shows the rethreading that must occur when Dave is removed from the skip list.

Figure 15. Deleting an element from a skip list
As with the Add(IComparable) method, Remove(IComparable) maintains an updates array that keeps track of the elements at each level that appear immediately before the element to be deleted. Once this updates array has been populated, the array is iterated through from the bottom up, and the elements in the array are rethreaded to point to the deleted element's references at the corresponding levels. The Remove(IComparable) method code follows.
public virtual void Remove(IComparable value)
{
Node [] updates = new Node[head.Height];
Node current = head;
int i = 0;
// first, determine the nodes that need to be updated at each level
for (i = head.Height - 1; i >= 0; i--)
{
while (current[i] != null && current[i].Value.CompareTo(value) < 0)
current = current[i];
updates[i] = current;
}
current = current[0];
if (current != null && current.Value.CompareTo(value) == 0)
{
count--;
// We found the data to delete
for (i = 0; i < head.Height; i++)
{
if (updates[i][i] != current)
break;
else
updates[i][i] = current[i];
}
// finally, see if we need to trim the height of the list
if (head[head.Height - 1] == null)
{
// we removed the single, tallest item... reduce the list height
head.DecrementHeight();
}
}
else
{
// the data to delete wasn't found. Either return or throw an exception
return;
}
}
The first for loop should look familiar. It's the same code found in Add(IComparable), used to populate the updates array. Once the updates array has been populated, we check to ensure that the element we reached does indeed contain the value to be deleted. If not, the Remove() method simply returns. You might opt to have it throw an exception of some sort, though. Assuming the element reached is the element to be deleted, the count member variable is decremented and the references are rethreaded. Lastly, if we deleted the element with the greatest height, then we should decrement the height of the head element. This is accomplished through a call to the DecrementHeight() method of the Node class.
Analyzing the running time
In "Skip Lists: A Probabilistic Alternative to Balanced Trees," Pugh provides a quick proof showing that the skip list's search, insertion, and deletion running times are asymptotically bounded by log2 n in the average case. However, a skip list can exhibit linear time in the worst case, but the likelihood of the worst-case scenario happening is extremely unlikely.
Since the heights of the elements of a skip list are randomly chosen, there is a chance that all, or virtually all, elements in the skip list will end up with the same height. For example, imagine that we had a skip list with 100 elements, all that happen to have height 1 chosen for their randomly selected height. Such a skip list would be, essentially, a normal linked list, not unlike the one shown in Figure 8. As we discussed earlier, the running time for operations on a normal linked list is linear.
While such worst-case scenarios are possible, realize that they are highly improbable. To put things in perspective, the likelihood of having a skip list with 100 height 1 elements is the same likelihood of flipping a coin 100 times and having it come up tails all 100 times. The chances of this happening are precisely 1 in 1,267,650,600,228,229,401,496,703,205,376. Of course with more elements, the probability goes down even further. For more information, be sure to read about Pugh's probabilistic analysis of skip lists in his paper.
Examining Some Empirical Results
Included in the article's download is the SkipList class, along with a testing Windows Forms application. With this testing application, you can manually add, remove, and inspect the list, and can see the nodes of the list displayed. Also, this testing application includes a "stress tester," where you can indicate how many operations to perform and an optional random seed value. The stress tester then creates a skip list, adds at least half as many elements as operations requested, and then, with the remaining operations, does a mix of inserts, deletes, and queries. At the end you can see review a log of the operations performed and their result, along with the skip list height, the number of comparisons needed for the operation, and the number of elements in the list.
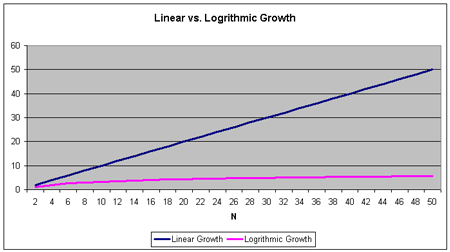
The graph in Figure 16 shows the average number of comparisons per operation for increasing skip list sizes. Note that as the skip list doubles in size, the average number of comparisons needed per operation only increases by a small amount (one or two more comparisons). To fully understand the utility of logarithmic growth, consider how the time for searching an array would fare on this graph. For a 256 element array, on average 128 comparisons would be needed to find an element. For a 512 element array, on average 256 comparisons would be needed. Compare that to the skip list, which for skip lists with 256 and 512 elements require only 9 and 10 comparisons on average!

Figure 16. Viewing the logarithmic growth of comparisons required for an increasing number of skip list elements.
Conclusion
In Part 3 of this article series, we looked at binary trees and binary search trees. BSTs provide an efficient log2 n running time in the average case. However, the running time is sensitive to the topology of the tree, and a tree with a suboptimal ratio of breadth to height can reduce the running time of a BST's operations to linear time.
To remedy this worst-case running time of BSTs, which could happen quite easily since the topology of a BST is directly dependent on the order with which items are added, computer scientists have been inventing a myriad of self-balancing BSTs, starting with the AVL tree created in the 1960s. While data structures such as the AVL tree, the red-black tree, and numerous other specialized BSTs offer log2 n running time in both the average and worst case, they require especially complex code that can be difficult to correctly create.
An alternative data structure that offers the same asymptotic running time as a self-balanced BST, is William Pugh's skip list. The skip list is a specialized, sorted link list, whose elements have a height associated with them. In this article we constructed a SkipList class and saw how straightforward the skip list's operations were, and how easy it was to implement them in code.
This fourth part of the article series is the last proposed part on trees. In the fifth installment, we'll look at graphs, which is a collection of vertexes with an arbitrary number of edges connecting each vertex to one another. As we'll see in Part 5, trees are a special form of graphs. Graphs have an extraordinary number of applications in real-world problems.
As always, if you have questions, comments, or suggestions for future material to discuss, I invite your comments! I can be reached at mitchell@4guysfromrolla.com.
Happy Programming!
References
- Cormen, Thomas H., Charles E. Leiserson, and Ronald L. Rivest. "Introduction to Algorithms." MIT Press. 1990.
- Pugh, William. "Skip Lists: A Probabilistic Alternative to Balanced Trees." Available online at ftp://ftp.cs.umd.edu/pub/skipLists/skiplists.pdf.
Related Books
- Combinatorial Algorithms, Enlarged Second Edition by Hu, T. C.
- Algorithms in C, Parts 1-5 (Bundle): Fundamentals by Sedgewick, Robert
Scott Mitchell, author of five books and founder of 4GuysFromRolla.com, has been working with Microsoft Web technologies for the past five years. Scott works as an independent consultant, trainer, and writer, and recently completed his Masters degree in Computer Science at the University of California – San Diego. He can be reached at mitchell@4guysfromrolla.com or through his blog at http://ScottOnWriting.NET.
Scott Mitchell
4GuysFromRolla.com
March 2004
Summary: A graph, like a tree, is a collection of nodes and edges, but has no rules dictating the connection among the nodes. In this fifth part of the article series, we'll learn all about graphs, one of the most versatile data structures. (26 printed pages)
Download the Graphs.msi sample file.
Contents
Introduction
Examining the Different Classes of Edges
Creating a C# Graph Class
A Look at Some Common Graph Algorithms
Conclusion
Related Books
Introduction
Part 1 and Part 2 of this article series focused on linear data structures—the array, the ArrayList, the Queue, the Stack, and the Hashtable. In Part 3, we began our investigation of trees. Recall that trees consist of a set of nodes, where all of the nodes share some connection to other nodes. These connections are referred to as edges. As we discussed, there are numerous rules as to how these connections can occur. For example, all nodes in a tree except for one—the root—must have precisely one parent node, while all nodes can have an arbitrary number of children. These simple rules ensure that, for any tree, the following three statements will hold true:
- Starting from any node, any other node in the tree can be reached. That is, there exists no node that can't be reached through some simple path.
- There are no cycles. A cycle exists when, starting from some node v, there is some path that travels through some set of nodes v1, v2, ..., vk that then arrives back at v.
- The number of edges in a tree is precisely one less than the number of nodes.
In Part 3 we focused on binary trees, which are a special form of trees. Binary trees are trees whose nodes have at most two children.
In this fifth installment of the article series we're going to examine graphs. Graphs are composed of a set of nodes and edges, just like trees, but with graphs there are no rules for the connections between nodes. With graphs, there is no concept of a root node, nor is there a concept of parents and children. Rather, a graph is a collection of interconnected nodes.
Note Realize that all trees are graphs. A tree is a special case of a graph in which all nodes are reachable from some starting node and one that has no cycles.
Figure 1 shows three examples of graphs. Notice that graphs, unlike trees, can have sets of nodes that are disconnected from other sets of nodes. For example, graph (a) has two distinct, unconnected sets of nodes. Graphs can also contain cycles. Graph (b) has several cycles. One cycle is the path from v1 to v2 to v4 and back to v1. Another one is from v1 to v2 to v3 to v5 to v4 and back to v1. (There are also cycles in graph (a).) Graph (c) does not have any cycles, as it has one less edge than it does number of nodes, and all nodes are reachable. Therefore, it is a tree.

Figure 1. Three examples of graphs
Many real-world problems can be modeled using graphs. For example, search engines like Google model the Internet as a graph, where Web pages are the nodes in the graph and the links among Web pages are the edges. Programs like Microsoft MapPoint that can generate driving directions from one city to another use graphs, modeling cities as nodes in a graph and the roads connecting the cities as edges.
Examining the Different Classes of Edges
Graphs, in their simplest terms, are a collection of nodes and edges, but there are different kinds of edges:
- Directed versus undirected edges
- Weighted versus unweighted edges
When talking about using graphs to model a problem, it is important to indicate the class of graph with which you are working. Is it a graph whose edges are directed and weighted, or one whose edges are undirected and weighted? In the next two sections, we'll discuss the differences between directed and undirected edges and weighted and unweighted edges.
Directed and Undirected Edges
The edges of a graph provide the connections between one node and another. By default, an edge is assumed to be bidirectional. That is, if there exists an edge between nodes v and u, it is assumed that one can travel from v to u and from u to v. Graphs with bidirectional edges are said to be undirected graphs because there is no implicit direction in their edges.
For some problems, though, an edge might infer a one-way connection from one node to another. For example, when modeling the Internet as a graph, a hyperlink from Web page v linking to Web page u would imply that the edge between v to u would be unidirectional. That is, that one could navigate from v to u, but not from u to v. Graphs that use unidirectional edges are said to be directed graphs.
When drawing a graph, bidirectional edges are drawn as a straight line, as shown in Figure 1. Unidirectional edges are drawn as an arrow, showing the direction of the edge. Figure 2 shows a directed graph where the nodes are Web pages for a particular Web site and a directed edge from u to v indicates that there is a hyperlink from Web page u to Web page v. Notice that both u links to v and v links to u, two arrows are used—one from v to u and another from u to v.

Figure 2. Model of pages making up a website
Weighted and Unweighted Edges
Typically graphs are used to model a collection of "things" and their relationship among these "things." For example, the graph in Figure 2 modeled the pages in a website and their hyperlinks. Sometimes, though, it is important to associate some cost with the connection from one node to another.
A map can be easily modeled as a graph, with the cities as nodes and the roads connecting the cities as edges. If we wanted to determine the shortest distance and route from one city to another, we first need to assign a cost from traveling from one city to another. The logical solution would be to give each edge a weight, such as how many miles it is from one city to another.
Figure 3 shows a graph that represents several cities in southern California. The cost of any particular path from one city to another is the sum of the costs of the edges along the path. The shortest path, then, would be the path with the least cost. In Figure 3, for example, a trip from San Diego to Santa Barbara is 210 miles if driving through Riverside, then to Barstow, and then to Santa Barbara. The shortest trip, however, is to drive 100 miles to Los Angeles, and then another 30 miles up to Santa Barbara.

Figure 3. Graph of California cities with edges valued as miles
Realize that the directionality and weight of edges are orthogonal. That is, a graph can have one of four arrangements of edges:
- Directed, weighted edges
- Directed, unweighted edges
- Undirected, weighted edges
- Undirected, unweighted edges
The graphs in Figure 1 had undirected, unweighted edges. Figure 2 had directed, unweighted edges, and Figure 3 used undirected, weighted edges.
Sparse Graphs and Dense Graphs
While a graph could have zero or a handful of edges, typically a graph will have more edges than it has nodes. What's the maximum number of edges a graph could have, given n nodes? It depends on whether the graph is directed or undirected. If the graph is directed, then each node could have an edge to every other node. That is, all n nodes could have n – 1 edges, giving a total of n * (n – 1) edges, which is nearly n2.
Note For this article, I am assuming nodes are not allowed to have edges to themselves. In general, though, graphs allow for an edge to exist from a node v back to node v. If self-edges are allowed, the total number of edges for a directed graph would be n 2.
If the graph is undirected, then one node, call it v1, could have an edge to each and every other node, or n – 1 edges. The next node, call it v2, could have at most n – 2 edges because an edge from v2 to already exists. The third node, v3, could have at most n – 3 edges, and so forth. Therefore, for n nodes, there would be at most (n – 1) + (n – 2) + ... + 1 edges. As you might have guessed, summed up this comes to [n * (n-1)] / 2, or exactly half as many edges as a directed graph.
If a graph has significantly less than n2 edges, the graph is said to be sparse. For example, a graph with n nodes and n edges, or even 2n edges would be said to be sparse. A graph with close to the maximum number of edges is said to be dense.
When using graphs in an algorithm it is important to know the ratio between nodes and edges. As we'll see later on in this article, the asymptotic running time operations performed on a graph is typically expressed in terms of the number of nodes and edges in the graph.
Creating a C# Graph Class
While graphs are a very common data structure used in a wide array of different problems, there is no built-in graph data structure in the .NET Framework. Part of the reason is because an efficient implementation of a Graph class depends on a number of factors specific to the problem at hand. For example, graphs are typically modeled in one of two ways:
- Adjacency list
- Adjacency matrix
These two techniques differ in how the nodes and edges of the graph are maintained internally by the Graph class. Let's examine both of these approaches and weigh the pros and cons of each method.
Representing a Graph Using an Adjacency List
In Part 3 we created a C# class for binary trees, called BinaryTree. Recall that each node in a binary tree was represented by a Node class. The Node class contained three properties:
- Value, which held the value of the node, an object
- Left, a reference to the
Node's left child - Right, a reference to the
Node's right child
Clearly the Node class and BinaryTree classes are not sufficient for a graph. First, the Node class for a binary tree allows for only two edges—a left and right child. For a more general graph, though, there could be an arbitrary number of edges emanating from a node. Also, the BinaryTree class contains a reference to a single node, the root. But with a graph, there is no single point of reference. Rather, the graph would need to know about all of its nodes.
One option, then, is to create a Node class that has as one of its properties an array of Node instances, which represent the Node's neighbors. Our Graph class would also have an array of Node instances, with one element for each of the nodes in the graphs. Such a representation is called an adjacency list because each node maintains a list of adjacent nodes. Figure 4 depicts an adjacency list representation in graphical form.

Figure 4. Adjacency list representation in graphical form
Notice that with an undirected graph, an adjacency list representation duplicated the edge information. For example, in adjacency list representation (b) in Figure 4, the node a has b in its adjacency list, and node b also has node a in its adjacency list.
Each node has precisely as many Nodes in its adjacency list as it has neighbors. Therefore, an adjacency list is a very space-efficient representation of a graph. You never store more data than needed. Specifically, for a graph with V nodes and E edges, a graph using an adjacency list representation will require V + E Node instances for a directed graph and V + 2E Node instances for an undirected graph.
While Figure 4 does not show it, adjacency lists can also be used to represent weighted graphs. The only addition is that for each Node n's adjacency list, each Node instance in the adjacency list needs to store the cost of the edge from n.
The one downside of an adjacency list is that determining if there is an edge from some node u to v requires that u's adjacency list be searched. For dense graphs, u will likely have many Nodes in its adjacency list. Determining if there is an edge between two nodes, then, takes linear time for dense adjacency list graphs. Fortunately, when using graphs we'll likely not need to determine if there exists an edge between two particular nodes. More often than not, we'll want to simply enumerate all the edges of a particular node.
Representing a Graph Using an Adjacency Matrix
An alternative method for representing a graph is to use an adjacency matrix. For a graph with n nodes, an adjacency matrix is an n x n two-dimensional array. For weighted graphs the array element (u, v) would give the cost of the edge between u and v (or, perhaps -1 if no such edge existed between u and v). For an unweighted graph, the array could be an array of Booleans, where a True at array element (u, v) denotes an edge from u to v and a False denotes a lack of an edge.
Figure 5 depicts how an adjacency matrix representation in graphical form.

Figure 5. Adjacency matrix representation in graphical form
Note that undirected graphs display symmetry along the adjacency matrix's diagonal. That is, if there is an edge from u to v in an undirected graph then there will be two corresponding array entries in the adjacency matrix: (u, v) and (v, u).
Since determining if an edge exists between two nodes is simply an array lookup, this can be determined in constant time. The downside of adjacency matrices is that they are space inefficient. An adjacency matrix requires an n2 element array, so for sparse graphs much of the adjacency matrix will be empty. Also, for undirected graphs half of the graph is repeated information.
While either an adjacency matrix or adjacency list would suffice as an underlying representation of a graph for our Graph class, let's move forward using the adjacency list model. I chose this approach primarily because it is a logical extension from the Node and BinaryTree classes that we've already created together.
Creating the Node Class
The Node class represents a single node in the graph. When working with graphs, the nodes typically represent some entity. Therefore, our Node class contains a Data property of type object that can be used to store any sort of data associated with the node. Furthermore, we'll need some way to easily identify nodes, so let's add a string Key property, which serves as a unique identifier for each Node.
Since we are using the adjacency list technique to represent the graph, each Node instance needs to have a list of its neighbors. If the graph uses weighted edges, the adjacency list also needs to store the weight of each edge. To manage this adjacency list, we'll first need to create an AdjacencyList class.
The AdjacencyList and EdgeToNeighbor classes
A Node contains an AdjacencyList class, which is a collection of edges to the Node's neighbors. Since an AdjacencyList stores a collection of edges, we first need to create a class that represents an edge. Let's call this class EdgeToNeighbor, since it models an edge that extends to a neighboring node. Since we might want to associate a weight with this edge, EdgeToNeighbor needs two properties:
- Cost, an integer value indicating the weight of the edge
- Neighbor, a Node reference
The AdjancencyList class, then, is derived from the System.Collections.CollectionBase class, and is simply a strongly-typed collection of EdgeToNeighbor instances. The code for EdgeToNeighbors and AdjacencyList is shown below:
public class EdgeToNeighbor
{
// private member variables
private int cost;
private Node neighbor;
public EdgeToNeighbor(Node neighbor) : this(neighbor, 0) {}
public EdgeToNeighbor(Node neighbor, int cost)
{
this.cost = cost;
this.neighbor = neighbor;
}
public virtual int Cost
{
get
{
return cost;
}
}
public virtual Node Neighbor
{
get
{
return neighbor;
}
}
}
public class AdjacencyList : CollectionBase
{
protected internal virtual void Add(EdgeToNeighbor e)
{
base.InnerList.Add(e);
}
public virtual EdgeToNeighbor this[int index]
{
get { return (EdgeToNeighbor) base.InnerList[index]; }
set { base.InnerList[index] = value; }
}
}
The Node class's Neighbors property exposes the Node's internal AdjacencyList member variable. Notice that the AdjacencyList class's Add() method is marked internal so that only classes in the assembly can add an edge to a Node's adjacency list. This is done so that the developer using the Graph class can only modify the graph's structure through the Graph class members and not indirectly through the Node's Neighbors property.
Adding edges to a node
In addition to its Key, Data, and Neighbors properties, the Node class needs to provide a method to allow the developer manipulating the Graph class to add an edge from itself to a neighbor. Recall that with the adjacency list approach, if there exists an undirected edge between nodes u and v, then u will have a reference to v in its adjacency list and v will have a reference to u in its adjacency list. Nodes should only be responsible for maintaining their own adjacency lists, and not that of others Nodes in the graph. As we'll see later, the Graph class contains methods to add either directed or undirected edges between two nodes.
To make the job of the Graph class adding an edge between two Nodes easier, the Node class contains a method for adding a directed edge from itself to some neighbor. This method, AddDirected(), takes in a Node instance and an optional weight, creates an EdgeToNeighbor instance, and adds it to the Node's adjacency list. The following code highlights this process:
protected internal virtual void AddDirected(Node n)
{
AddDirected(new EdgeToNeighbor(n));
}
protected internal virtual void AddDirected(Node n, int cost)
{
AddDirected(new EdgeToNeighbor(n, cost));
}
protected internal virtual void AddDirected(EdgeToNeighbor e)
{
neighbors.Add(e);
}
Building the Graph Class
Recall that with the adjacency list technique, the graph maintains a list of its nodes. Each node, then, maintains a list of adjacent nodes. So, in creating the Graph class we need to have a list of Nodes. We could opt to use an ArrayList to maintain this list, but a more efficient approach would be to use a Hashtable. A Hashtable here is a more sensible approach because in the methods used to add an edge in the Graph class, we'll need to make sure that the two Nodes specified to add an edge between both exist in the graph. With an ArrayList we'd have to linearly search through the array to find both Node instances; with a Hashtable we can take advantage of a constant-time lookup. (For more information on Hashtables and their asymptotic running times, read Part 2 of the article series.)
The NodeList class, shown below, contains strongly-typed Add() and Remove() methods for adding and removing Node instances from the graph. It also has a ContainsKey() method, which determines if a particular Node Key value already exists in the graph.
public class NodeList : IEnumerable
{
// private member variables
private Hashtable data = new Hashtable();
// methods
public virtual void Add(Node n)
{
data.Add(n.Key, n);
}
public virtual void Remove(Node n)
{
data.Remove(n.Key);
}
public virtual bool ContainsKey(string key)
{
return data.ContainsKey(key);
}
public virtual void Clear()
{
data.Clear();
}
// Properties...
public virtual Node this[string key]
{
get
{
return (Node) data[key];
}
}
// ... some methods and properties removed for brevity ...
}
The Graph class contains a public property Nodes, which is of type NodeList. Additionally, the Graph class has a number of methods for adding directed or undirected, and weighted or unweighted edges between two existing nodes in the graph. The AddDirectedEdge() method takes in two Nodes and an optional weight, and creates a directed edge from the first Node to the second. Similarly, the AddUndirectedEdge() method takes in two Nodes and an optional weight, adding a directed edge from the first to the second Node, as well as a directed edge from the second back to the first Node.
In addition to its methods for adding edges, the Graph class has a Contains() method that returns a Boolean indicating if a particular Node exists in the graph or not. The germane code for the Graph class is shown below:
public class Graph
{
// private member variables
private NodeList nodes;
public Graph()
{
this.nodes = new NodeList();
}
public virtual Node AddNode(string key, object data)
{
// Make sure the key is unique
if (!nodes.ContainsKey(key))
{
Node n = new Node(key, data);
nodes.Add(n);
return n;
}
else
throw new ArgumentException("There already exists a node
in the graph with key " + key);
}
public virtual void AddNode(Node n)
{
// Make sure this node is unique
if (!nodes.ContainsKey(n.Key))
nodes.Add(n);
else
throw new ArgumentException("There already exists a node
in the graph with key " + n.Key);
}
public virtual void AddDirectedEdge(string uKey, string vKey)
{
AddDirectedEdge(uKey, vKey, 0);
}
public virtual void AddDirectedEdge(string uKey, string vKey, int cost)
{
// get references to uKey and vKey
if (nodes.ContainsKey(uKey) && nodes.ContainsKey(vKey))
AddDirectedEdge(nodes[uKey], nodes[vKey], cost);
else
throw new ArgumentException("One or both of the nodes
supplied were not members of the graph.");
}
public virtual void AddDirectedEdge(Node u, Node v)
{
AddDirectedEdge(u, v, 0);
}
public virtual void AddDirectedEdge(Node u, Node v, int cost)
{
// Make sure u and v are Nodes in this graph
if (nodes.ContainsKey(u.Key) && nodes.ContainsKey(v.Key))
// add an edge from u -> v
u.AddDirected(v, cost);
else
// one or both of the nodes were not found in the graph
throw new ArgumentException("One or both of the nodes
supplied were not members of the graph.");
}
public virtual void AddUndirectedEdge(string uKey, string vKey)
{
AddUndirectedEdge(uKey, vKey, 0);
}
public virtual void AddUndirectedEdge(string uKey, string vKey, int cost)
{
// get references to uKey and vKey
if (nodes.ContainsKey(uKey) && nodes.ContainsKey(vKey))
AddUndirectedEdge(nodes[uKey], nodes[vKey], cost);
else
throw new ArgumentException("One or both of the nodes
supplied were not members of the graph.");
}
public virtual void AddUndirectedEdge(Node u, Node v)
{
AddUndirectedEdge(u, v, 0);
}
public virtual void AddUndirectedEdge(Node u, Node v, int cost)
{
// Make sure u and v are Nodes in this graph
if (nodes.ContainsKey(u.Key) && nodes.ContainsKey(v.Key))
{
// Add an edge from u -> v and from v -> u
u.AddDirected(v, cost);
v.AddDirected(u, cost);
}
else
// one or both of the nodes were not found in the graph
throw new ArgumentException("One or both of the nodes
supplied were not members of the graph.");
}
public virtual bool Contains(Node n)
{
return Contains(n.Key);
}
public virtual bool Contains(string key)
{
return nodes.ContainsKey(key);
}
public virtual NodeList Nodes
{
get
{
return this.nodes;
}
}
}
Notice that the AddDirectedEdge() and AddUndirectedEdge() methods check to ensure that the Nodes passed in exist in the graph. If they do not, an ArgumentException is thrown. Also note that these two methods have a number of overloads. You can add two nodes by passing in Node references or the Nodes' Key values.
Using the Graph Class
At this point we have created all of the classes needed for our graph data structure. We'll soon turn our attention to some of the more common graph algorithms, such as constructing a minimum spanning tree and finding the shortest path from a single node to all other nodes. But before we, do let's examine how to use the Graph class in a C# application.
Once we create an instance of the Graph class, the next task is to add the Nodes to the graph. This involves calling the AddNode() method of the Graph class for each node to add to the graph. Let's recreate the graph from Figure 2. We'll need to start by adding six nodes. For each of these nodes let's have the Key be the Web page's filename. We'll leave the Data as null, although this might conceivably contain the contents of the file, or a collection of keywords describing the Web page content.
Graph web = new Graph();
web.AddNode("Privacy.htm", null);
web.AddNode("People.aspx", null);
web.AddNode("About.htm", null);
web.AddNode("Index.htm", null);
web.AddNode("Products.aspx", null);
web.AddNode("Contact.aspx", null);
Next we need to add the edges. Since this is a directed, unweighted graph, we'll use the AddDirectedEdge(u, v) method of the Graph class to add an edge from u to v.
web.AddDirectedEdge("People.aspx", "Privacy.htm"); // People -> Privacy
web.AddDirectedEdge("Privacy.htm", "Index.htm"); // Privacy -> Index
web.AddDirectedEdge("Privacy.htm", "About.htm"); // Privacy -> About
web.AddDirectedEdge("About.htm", "Privacy.htm"); // About -> Privacy
web.AddDirectedEdge("About.htm", "People.aspx"); // About -> People
web.AddDirectedEdge("About.htm", "Contact.aspx"); // About -> Contact
web.AddDirectedEdge("Index.htm", "About.htm"); // Index -> About
web.AddDirectedEdge("Index.htm", "Contact.aspx"); // Index -> Contacts
web.AddDirectedEdge("Index.htm", "Products.aspx"); // Index -> Products
web.AddDirectedEdge("Products.aspx", "Index.htm"); // Products -> Index
web.AddDirectedEdge("Products.aspx", "People.aspx");// Products -> People
After these commands, web represents the graph shown in Figure 2. Once we have constructed a graph, we'll want to answer some questions. For example, for the graph we just created, we might want to ask, "What's the least number of links a user must click to reach any Web page when starting from the homepage (Index.htm)?" To answer such questions, we can usually fall back on using existing graph algorithms. In the next section we'll examine two common algorithms for weighted graphs:
- Constructing a minimum spanning tree
- Finding the shortest path from one node to all others
A Look at Some Common Graph Algorithms
Because graphs are a data structure that can be used to model a bevy of real-world problems, there are unlimited numbers of algorithms designed to find solutions for common problems. To further our understanding of graphs, let's take a look at two of the most studied applications of graphs.
The Minimum Spanning Tree Problem
Imagine that you work for the phone company and your task is to provide phone lines to a village with 10 houses, each labeled H1 through H10. Specifically this involves running a single cable that connects each home. That is, the cable must run through houses H1, H2, and so forth, up through H10. Due to geographic obstacles like hills, trees, rivers, and so on, it is not feasible to run the cable from one house to another.
Figure 6 shows this problem depicted as a graph. Each node is a house, and the edges are the means by which one house can be wired up to another. The weights of the edges dictate the distance between the homes. Your task is to wire up all ten houses using the least amount of telephone wiring possible.

Figure 6. Graphical representation of hooking up a 10-home village with phone lines
For a connected, undirected graph, there exists some subset of the edges that connect all the nodes and does not introduce a cycle. Such a subset of edges would form a tree (since it would comprise one less edge than vertices and is acyclic), and is called a spanning tree. There are typically many spanning trees for a given graph. Figure 7 shows two valid spanning trees from the Figure 6 graph. (The edges forming the spanning tree are bolded.)

Figure 7.Spanning tree subsets based on Figure 6
For graphs with weighted edges, different spanning trees have different associated costs, where the cost is the sum of the weights of the edges that comprise the spanning tree. A minimum spanning tree, then, is the spanning tree with a minimum cost.
There are two basic approaches to solving the minimum spanning tree problem. One approach is build up a spanning tree by choosing the edges with the minimum weight, so long as adding that edge does not create a cycle among the edges chosen thus far. This approach is shown in Figure 8.

Figure 8. Minimum spanning tree that uses the edges with the minimum weight
The other approach builds up the spanning tree by dividing the nodes of the graph into two disjoint sets: the nodes currently in the spanning tree and those nodes not yet added. At each iteration, the least weighted edge that connects the spanning tree nodes to a node in the spanning tree is added to the spanning tree. To start off the algorithm, some random start node must be selected. Figure 9 illustrates this approach in action, using H1 as the starting node. (In Figure 9 those nodes that are in the set of nodes in the spanning tree are shaded light yellow.)

Figure 9. Prim method of finding the minimum spanning tree
Notice that the techniques illustrated in Figure 8 and Figure 9 arrived at the same minimum spanning tree. If there is only one minimum spanning tree for the graph, then both of these approaches will reach the same conclusion. If, however, there are multiple minimum spanning trees, these two approaches might arrive with different results (both results will be correct, naturally).
Note The first approach we examined was discovered by Joseph Kruskal in 1956 at Bell Labs. The second technique was discovered in 1957 by Robert Prim, also a researcher at Bell Labs. There is a plethora of information on these two algorithms on the Web, including Java applets showing the algorithms in progress graphically ( Kruskal's Algorithm | Prim's Algorithm), as well as source code in a variety of languages.
Computing the Shortest Path from a Single Source
When flying from one city to another, part of the headache is finding a route that requires the fewest number of connections. No one likes their flight from New York to Los Angeles to go from New York to Chicago, then Chicago to Denver, and finally Denver to Los Angeles. Most people would rather have a direct flight straight from New York to Los Angeles.
Imagine, however, that you are not one of those people. Instead, you are someone who values his money much more than his time, and are most interested in finding the cheapest route, regardless of the number of connections. This might mean flying from New York to Miami, then Miami to Dallas, then Dallas to Phoenix, Phoenix to San Diego, and finally San Diego to Los Angeles.
We can solve this problem by modeling the available flights and their costs as a directed, weighted graph. Figure 10 shows such a graph.

Figure 10. Modeling of available flights based on cost
What we are interested in knowing is what is the shortest path from New York to Los Angeles. By inspecting the graph, we can quickly determine that it's from New York to Chicago to San Francisco and finally down to Los Angeles, but in order to have a computer accomplish this task we need to formulate an algorithm to solve the problem at hand.
Edgar Dijkstra, one of the most noted computer scientists of all time, invented the most commonly used algorithm for finding the shortest path from a source node to all other nodes in a weighted, directed graph. This algorithm, dubbed Dijkstra's Algorithm, works by maintaining two tables, each of which has a record for each node. These two tables are:
- A distance table, which keeps an up-to-date "best distance" from the source node to every other node.
- A route table, which, for each node n, indicates what node was used to reach n to get the best distance.
Initially, the distance table has each record set to some high value (like positive infinity) except for the start node, which has a distance to itself of 0. The route table's rows are all set to null. Also, a collection of nodes, Q, that need to be examined is maintained; initially, this collection contains all of the nodes in the graph.
The algorithm proceeds by selecting (and removing) the node from Q that has the lowest value in the distance table. Let this selected node be called n and the value in the distance table for n is d. For each of the n's edges, a check is made to see if d plus the cost to get from n to that particular neighbor is less than the value for that neighbor in the distance table. If it is, then we've found a better way to reach that neighbor, and the distance and route tables are updated accordingly.
To help clarify this algorithm, let's begin applying it to the graph from Figure 10. Since we want to know the cheapest route from New York to Los Angeles we use New York as our source node. Our initial distance table, then, contains a value of infinity for each of the other cities, and a value of 0 for New York. The route table contains nulls for all entries, and Q contains all nodes (see Figure 11).

Figure 11. Distance table and route table for determining cheapest fare
Now, we start by extracting the city from Q that has the lowest value in the distance table, which is New York. We then examine each of New York's neighbors and check to see if the cost to fly from New York to that neighbor is less than the best cost we know of, namely the cost in the distance table. After this first check, we'd have removed New York from Q and updated the distance and route tables for Chicago, Denver, Miami, and Dallas.

Figure 12. Step 2 in the process of determining the cheapest fare
The next iteration gets the cheapest city out of Q, Chicago, and then checks its neighbors to see if there is a better cost. Specifically, we'll check to see if there's a better route for getting to San Francisco or Denver. Clearly the cost to get to San Francisco from Chicago—$75 + $25Los Angeles is less than Infinity, so San Francisco's records are updated. Also, note that it is cheaper to fly from Chicago to Denver than from New York to Denver ($75 + $20 < $100), so Denver is updated as well. Figure 13 shows the values of the tables and Q after Chicago has been processed.

Figure 13. Table status after the third leg of the process is finished
This process continues until there are no more nodes in Q. Figure 14 shows the final values of the tables when Q has been exhausted.

Figure 14. Final results of determining the cheapest fare
At the point of exhausting Q, the distance table contains the lowest cost from New York to each city. To determine the flight path to arrive at L.A., start by examining the L.A. entry in the route table and work back up to New York. That is, the route table entry for L.A. is San Francisco, meaning the last leg of the flight to L.A. leaves from San Francisco. The route table entry for San Francisco is Chicago, meaning you'll get to San Francisco through Chicago. Finally, Chicago's route table entry is New York. Putting this together we see that the flight path is from New York to Chicago to San Francisco to L.A.
Note To see a working implementation of Dijkstra's Algorithm in C#, check out the download for this article, which includes a testing application for the Graph class that determines the shortest distance from one city to another using Dijkstra's Algorithm.
Conclusion
Graphs are a commonly used data structure because they can be used to model many real-world problems. A graph consists of a set of nodes with an arbitrary number of connections, or edges, between the nodes. These edges can be either directed or undirected and weighted or unweighted.
In this article, we examined the basics of graphs and created a Graph class. This class was similar to the BinaryTree class created in Part 3, the difference being that instead of only have a reference for at most two edges, the Nodes of the Graph class could have an arbitrary number of references. This similarity is not surprising because trees are a special case of graphs.
In addition to creating a Graph class, we also looked at two common graph algorithms, the minimum spanning tree problem, and computing the shortest path from some source node to all other nodes in a weighted, directed graph. While we did not examine source code to implement these algorithms, there are plenty source-code examples available on the Internet. Also, the download included with this article contains a testing application for the Graph class that uses Dijkstra's Algorithm to compute the shortest route between two cities.
In the next installment, Part 6, we'll look at efficiently maintaining disjoint sets. Disjoint sets are a collection of two or more sets that do not share any elements in common. For example, with Prim's Algorithm for finding the minimum spanning tree, the nodes of the graph can be divided into two disjoint sets—the set of nodes that currently constitute the spanning tree and the set of nodes that are not yet in the spanning tree.
Related Books
- Introduction to Algorithms by Thomas H. Cormen
Scott Mitchell, author of five books and founder of 4GuysFromRolla.com, has been working with Microsoft Web technologies for the past five years. Scott works as an independent consultant, trainer, and writer, and recently completed his Masters degree in Computer Science at the University of California – San Diego. He can be reached at mitchell@4guysfromrolla.com or through his blog at http://ScottOnWriting.NET.
Scott Mitchell
4GuysFromRolla.com
April 2004
Summary: Scott Mitchell discusses data structures for implementing general and disjoint sets. A set is an unordered collection of unique items that can be enumerated and compared to other sets in a variety of ways. (20 printed pages)
Download the Sets.msi sample file.
Contents
Introduction
The Fundamentals of Sets
Implementing an Efficient Set Data Structure
Maintaining a Collection of Disjoint Sets
References
Related Books
Introduction
One of the most basic mathematical constructs is a set, which is an unordered collection of unique objects. The objects contained within a set are referred to as the set's elements. Formally, a set is denoted as a capital, italic letter, with its elements appearing within curly braces ({...}). Examples of this notation can be seen below:
S = { 1, 3, 5, 7, 9 }
T = { Scott, Jisun, Sam }
U = { -4, 3.14159, Todd, x }
In mathematics, sets are typically comprised of numbers, such as set S above, which contains the odd positive integers less than 10. However, notice that the elements of a set can be anything—numbers, people, strings, letters, variables, and so on. Set T, for example, contains peoples' names, and set U contains a mix of numbers, names, and variables.
In this article, we'll start with a basic introduction of sets, including common notation and the operations that can be performed on sets. Following that, we'll examine how to efficiently implement a set data structure with a defined universe. The article concludes with an examination of disjoint sets, and the best data structures to use.
The Fundamentals of Sets
Recall that a set is simply a collection of elements. The "element of" operator, denoted x Î S, implies that x is an element in the set S. For example, if set S contains the odd positive integers less than 10, then 1Î S. When reading such notation, you'd say, "1 is an element of S." In addition to 1 being an element of S, we have 3 Î S, 5 Î S, 7 Î S, and 9 Î S. The "not an element of" operator, denoted x Ï S, means that x is not an element of set S.
The number of unique elements in a set is the set's cardinality. The set {1, 2, 3} has cardinality 3, just as does the set {1, 1, 1, 1, 1, 1, 1, 2, 3} (because it only has three unique elements). A set may have no elements in it at all. Such a set is called the empty set, and is denoted as {} or Æ, and has a cardinality of 0.
When first learning about sets, many developers assume they are the same as collections, like an ArrayList. However, there are some subtle differences. An ArrayList is an ordered collection of elements—each element in an ArrayList has an associated ordinal index, which implies order. Too, there can be duplicate elements in an ArrayList.
A set, on the other hand, is unordered and contains unique items. Since sets are unordered, the elements of a set may be listed in any order. That is, the sets {1, 2, 3} and {3, 1, 2} are considered equivalent. Also, any duplicates in a set are considered redundant. The set {1, 1, 1, 2, 3} and the set {1, 2, 3} are equivalent. Two sets are equivalent if they have the same elements. (Equivalence is denoted with the = sign; if S and T are equivalent they are written as S = T.)
Note In mathematics, an ordered collection of elements that allows duplicates is referred to as a list. Two lists, L 1 and L 2 are considered equal if and only if for i ranging from 1 to the number of elements in the list the ith element in L 1 equals the ith element in L 2.
Typically the elements that can appear in a set are restricted to some universe. The universe is the set of all possible values that can appear in a set. For example, we might only be interested in working with sets whose universe are integers. By restricting the universe to integers, we can't have a set that has a non-integer element, like 8.125, or Sam. (The universe is denoted as the set U.)
Relational Operators of Sets
There are a bevy of relational operators that are commonly used with numbers. Some of the more often used ones, especially in programming languages, include <, <=, =, !=, >, and >=. A relational operator determines if the operand on the left hand side is related to the operand on the right hand side based on criteria defined by the relational operator. Relational operators return a "true" or "false" value, indicating whether or not the relationship holds between the operands. For example, x < y returns true if x is less than y, and false otherwise. (Of course the meaning of "less than" depends on the data type of x and y.)
Relational operators like <, <=, =, !=, >, and >= are typically used with numbers. Sets, as we've seen, use the = relational operator to indicate that two sets are equivalent (and can likewise use != to denote that two sets are not equivalent), but relational operators <, <=, >, and >= are not defined for sets. After all, how is one to determine if the set {1, 2, 3} is less than the set {Scott, 3.14159}?
Instead of notions of < and <=, sets use the relational operators subset and proper subset, denoted Í and Ì, respectively. (Some older texts will use Ì for subset and Í for proper subset.) S is a subset of T—denoted S Í T—if every element in S is in T. That is, S is a subset of T if it is contained within T. If S = {1, 2, 3}, and T = {0, 1, 2, 3, 4, 5}, then S Í T since every element in S—1, 2 and 3—is an element in T. S is a proper subset of T—denoted S Ì T—if S Í T and S ¹ T. That is, if S = {1, 2, 3} and T = {1, 2, 3}, then S Í T since every element in S is an element in T, but S T since S = T. (Notice that there is a similarity between the relational operators < and <= for numbers and the relational operators Í and Ì for sets.)
Using the new subset operator, we can more formally define set equality. Given sets S and T, S = T if and only if S Í T and T Í S. In English, S and T are equivalent if and only if every element in S is in T, and every element in T is in S.
Note Since Í is analogous to<=, it would make sense that there exists a set relational operator analogous to>=. This relational operator is called superset, and is denoted Ê; a proper superset is denoted . Like with<=and>=, S Ê T if and only if T Í S.
Set Operations
As with the relational operators, many operations defined for numbers don't translate well to sets. Common operations on numbers include addition, multiplication, subtraction, exponentiation, and so on. For sets, there are four basic operations:
- Union – the union of two sets, denoted S È T, is akin to addition for numbers. The union operator returns a set that contains all of the elements in S and all of the elements in T. For example, {1, 2, 3} È {2, 4, 6} equals {1, 2, 3, 2, 4, 6}. (The duplicate 2 can be removed to provide a more concise answer, yielding {1, 2, 3, 4, 6}.) Formally, S È T = {x : x Î S or x Î T}. In English, this translates to S union T results in the set that contains an element x if x is in S or in T.
- Intersection – the intersection of two sets, denoted S Ç T, is the set of elements that S and T have in common. For example, {1, 2, 3} Ç {2, 4, 6} equals {2}, since that's the only element both {1, 2, 3} and {2, 4, 6} share in common. Formally, S Ç T = {x : x Î S and x Î T}. In English, this translates to S intersect T results in the set that contains an element x if x is both in S and in T.
- Difference – the difference of two sets, denoted S - T, are all of the elements in S that are not in T. For example, {1, 2, 3} - {2, 4, 6} equals {1, 3}, since 1 and 3 are the elements in S that are not in T. Formally, S - T = {x : x Î S and x Ï T}. In English, this translates to S set difference T results in the set that contains an element x if x is in S and not in T.
- Complement – Earlier we discussed how typically sets are limited to a known universe of possible values, such as the integers. The complement of a set, denoted S', is U - S. (Recall that U is the universe set.) If our universe is the integers 1 through 10, and S = {1, 4, 9, 10}, then S' = {2, 3, 5, 6, 7, 8}. (Complementing a set is akin to negating a number. Just like negating a number twice will give you the original number back—that is, --x = x—complementing a set twice will give you the original set back—S'' = S.)
When examining new operations, it is always important to get a solid grasp on the nature of the operations. Some questions to ask yourself when learning about any operation—be it one defined for numbers or one defined for sets—are:
- Is the operation commutative? An operator op is commutative if x op y is equivalent to y op x. In the realm of numbers, addition is an example of a commutative operator, while division is not commutative.
- Is the operation associative? That is, does the order of operations matter. If an operator op is associative, then x op (y op z) is equivalent to (x op y) op z. Again, in the realm of numbers addition is associative, but division is not.
For sets, the union and intersection operations are both commutative and associative. S È T is equivalent to T È S, and S È (T È V) is equivalent to (S È T) È V. Set difference, however, is neither commutative nor associative. (To see that set difference is not commutative, consider that {1, 2, 3} - {3, 4, 5} = {1, 2}, but {3, 4, 5} - {1, 2, 3} = {4, 5}.)
Finite Sets and Infinite Sets
All of the set examples we've looked at thus far have dealt with finite sets. A finite set is a set that has a finite number of elements. While it may seem counterintuitive at first, a set can contain an infinite number of elements. The set of positive integers, for example, is an infinite set since there are no bounds to the number of elements in the set.
In mathematics, there are a couple infinite sets that are used so often that they are given a special symbol to represent them. These include:
- N = {0, 1, 2, …}
- Z = {…, -2, -1, 0, 1, 2, …}
- Q = {a/b: a Î Z, b Î Z, and b ¹ 0}
- R = set of real numbers
N is the set of natural numbers, or positive integers greater than or equal to 0. Z is the set of integers. Q is the set of rational numbers, which are numbers that can be expressed as a fraction of two integers. Finally, R is the set of real numbers, which are all rational numbers, plus irrational numbers as well (numbers that cannot be expressed as a fraction of two integers, such as pi, and the square root of 2).
Infinite sets, of course, can't be written down in their entirety, as you'd never finish jotting down the elements, but instead are expressed more tersely using mathematical notation like so:
S = {x : xÎ N and x > 100}
Here S would be the set of all natural numbers greater than 100.
In this article we will be looking at data structures for representing finite sets. While infinite sets definitely have their place in mathematics, rarely will we need to work with infinite sets in a computer program. Too, there are unique challenges with representing and operating upon infinite sets, since an infinite set's contents cannot be completely stored in a data structure or enumerated.
Note Computing the cardinality of finite sets is simple—just count up the number of elements. But how does one compute the cardinality of an infinite set? This discussion is beyond the scope of this article, but realize that there are different types of cardinality for infinite sets. Interestingly, there is the same "number" of positive integers, as there are all integers, but there are more real numbers than there are integers.
Sets in Programming Languages
C++, C#, Visual Basic .NET, and Java don't provide inherent language features for working with sets. If you want to use sets, you need to create your own set class with the appropriate methods, properties, and logic. (We'll do precisely this in the next section!) There have been programming languages in the past, though, that have offered sets as a fundamental building block in the language. Pascal, for example, provides a set construct that can be used to create sets with an explicitly defined universe. To work with sets, Pascal provides the in operator to determine if an element is in a particular set. The operators +, *, and – are used for union, intersection, and set difference. The following Pascal code illustrates the syntax used to work with sets:
/* declares a variable named possibleNumbers, a set whose universe is
the set of integers between 1 and 100... */
var
possibleNumbers = set of 1..100;
...
/* Assigns the set {1, 45, 23, 87, 14} to possibleNumbers */
possibleNumbers := [1, 45, 23, 87, 14];
/* Sets possibleNumbers to the union of possibleNumbers and {3, 98} */
possibleNumbers := possibleNumbers + [3, 98];
/* Checks to see if 4 is an element of possible numbers... */
if 4 in possibleNumbers then write("4 is in the set!");
Other previous languages have allowed for more powerful set semantics and syntax. A language called SETL (an acronym for SET Language) was created in the 70s and offered sets as a first-class citizen. Unlike Pascal, when using sets in SETL you are not restricted to specifying the set's universe.
Implementing an Efficient Set Data Structure
In this section we'll look at creating a class that provides the functionality and features of a set. When creating such a data structure, one of the first things we need to decide is how to store the elements of the set. This decision can greatly affect the asymptotic efficiency of the operations performed on the set data structure. (Keep in mind that the operations we'll need to perform on the set data structure include: union, intersection, set difference, subset, and element of.)
To illustrate how storing the set's elements can affect the run time, imagine that we created a set class that used an underlying ArrayList to hold the elements of the set. If we had two sets, S1 and S2 that we wanted to union (where S1 had m elements and S2 had n elements), we'd have to perform the following steps:
- Create a new set class, T, that holds the union of S1 and S2
- Iterate through the elements of S1, adding it to T.
- Iterate through the elements of S2. If the element does not already exist in T, then add it to T.
How many steps would performing the union take? Step (2) would require m steps through S1's m elements. Step (3) would take n steps, and for each element in S2, we'd have to determine if the element was in T. Using unsorted ArrayLists, to determine if an element is in an ArrayList the entire ArrayList must be enumerated linearly. So, for each of the n elements in S2 we might have to search through the m elements in T. This would lead to a quadratic running time for union of O(m * n).
The reason a union with an ArrayList takes quadratic time is because determining if an element exists within a set takes linear time. That is, to determine if an element exists in a set, the set's ArrayList must be exhaustively searched. If we could reduce the running time for the "element of" operation to a constant, we could improve the union's running time to a linear O(m + n). Recall from Part 2 of this article series that a Hashtable provides constant running time to determine if an item resides within the Hashtable. Hence, a Hashtable would be a better choice for storing the set's elements than an ArrayList.
If we require that the set's universe be known, we can implement an even more efficient set data structure using a bit array. Assume that the universe consists of elements e1, e2, …, ek. Then we can denote a set with a k-element bit array; if the ith bit is 1, then the element ei is in the set; if, on the other hand, the ith bit is 0, then the element ei is not in the set. Representing sets as a bit array not only provides tremendous space savings, but also enables efficient set operations, as these set-based operations can be performed using simple bit-wise instructions. For example, determining if element ei exists in a set takes constant time since only the ith bit in the bit array needs to be checked. The union of two sets is simply the bit-wise OR of the sets' bit arrays; the intersection of two sets is the bit-wise AND of the sets' bit arrays. Set difference and subset can be reduced down to bit-wise operations as well.
Note A bit array is a compact array composed of 1s and 0s, typically implemented as an integer array. Since an integer in the Microsoft .NET Framework has 32 bits, a bit array can store 32 bit values in one element of an integer array (rather than requiring 32 array elements).
Bit-wise operations are ones that are performed on the individual bits of an integer. There are both binary bit-wise operators and unary bit-wise operators. The bit-wise AND and bit-wise OR operators are binary, taking in two bits each, and returning a single bit. Bit-wise AND returns 1 only if both inputs are 1, otherwise it returns 0. Bit-wise OR returns 0 only if both inputs are 0, otherwise it returns 1.
For a more in-depth look at bit-wise operations in C# be sure to read: Bit-Wise Operators in C#.
Let's look at how to implement a set class that uses C#'s bit-wise operations.
Creating the PascalSet Class
Understand that to implement a set class that uses the efficient bit-wise operators the set's universe must be known. This is akin to the way Pascal uses sets, so in honor of the Pascal programming language I have decided to name this set class the PascalSet class. PascalSet restricts the universe to a range of integers or characters (just like the Pascal programming language). This range can be specified in the PascalSet's constructor.
public class PascalSet : ICloneable, ICollection
{
// Private member variables
private int lowerBound, upperBound;
private BitArray data;
public PascalSet(int lowerBound, int upperBound)
{
// make sure lowerbound is less than or equal to upperbound
if (lowerBound > upperBound)
throw new ArgumentException("The set's lower bound cannot be
greater than its upper bound.");
this.lowerBound = lowerBound;
this.upperBound = upperBound;
// Create the BitArray
data = new BitArray(upperBound - lowerBound + 1);
}
...
}
So, to create a PascalSet whose universe is the set of integers between -100 and 250, the following syntax could be used:
PascalSet mySet = new PascalSet(-100, 250);
Implementing the Set Operations
PascalSet implements the standard set operations—union, intersection, and set difference—as well as the standard relational operators—subset, proper subset, superset, and proper superset. The set operations union, intersection, and set difference, all return a new PascalSet instance, which contains the result of unioning, intersecting, or set differencing. The following code for the Union(PascalSet) method illustrates this behavior:
public virtual PascalSet Union(PascalSet s)
{
if (!AreSimilar(s))
throw new ArgumentException("Attempting to union two dissimilar
sets. Union can only occur between two sets with the same universe.");
// do a bit-wise OR to union together this.data and s.data
PascalSet result = new PascalSet(this.lowerBound, this.upperBound);
result.data = this.data.Or(s.data);
return result;
}
public static PascalSet operator +(PascalSet s, PascalSet t)
{
return s.Union(t);
}
The AreSimilar(PascalSet) method determines if the PascalSet passed has the same lower and upper bounds as the PascalSet instance. Therefore, union (and intersection and set difference) can only be applied to two sets with the same universe. (You could make a modification to the code here to have the returned PascalSet's universe be the union of the two universe sets, thereby allowing sets with non-disjoint universes to be unioned.) If the two PascalSets have the same universe, then a new PascalSet—result—is created with the same universe and its BitArray member variable—data—is assigned to the bit-wise OR of the two PascalSets' BitArrays. Notice that the PascalSet class also overloads the + operator for union (just like the Pascal programming language).
Enumerating the PascalSet's Members
Since sets are an unordered collection of elements, it would not make sense to have PascalSet implement IList, as collections that implement IList imply that the list has some ordinal order. Since PascalSet is a collection of elements, though, it makes sense to have it implement ICollection. Since ICollection implements IEnumerable, PascalSet needs to provide a GetEnumerator() method that returns an IEnumerator instance allowing a developer to iterate through the set's elements.
Oftentimes when creating a specialized collection class that uses some other underlying collection class to hold the data, the GetEnumerator() method for the specialized class can simply return the IEnumerator from the underlying collection's GetEnumerator() method. Since the PascalSet uses a BitArray to represent what elements are in the set, it might at first seem plausible to have PascalSet's GetEnumerator() method return the IEnumerator from the internal BitArray's GetEnumerator() method. However, the BitArray's GetEnumerator() returns an IEnumerator that enumerates all of the bits in the BitArray, returning a Boolean value for each bit—true if the bit is 1, false if the bit is 0.
The elements in the PascalSet, however, are only those elements where the BitArray's bit is 1. Therefore we need to create a custom class that implements IEnumerator and that intelligently walks the BitArray, only returning those elements whose corresponding bit in the BitArray is 1. To handle this I created a class within the PascalSet class called PascalSetEnumerator. This class's constructor takes in the current PascalSet instance as a sole input parameter. In the MoveNext() method it steps through the BitArray until it finds a bit with a value of 1.
class PascalSetEnumerator : IEnumerator
{
private PascalSet pSet;
private int position;
public PascalSetEnumerator(PascalSet pSet)
{
this.pSet = pSet;
position = -1;
}
...
public bool MoveNext()
{
// increment position
position++;
// see if there is another element greater than position
for (int i = position; i < pSet.data.Length; i++)
{
if (pSet.data.Get(i))
{
position = i;
return true;
}
}
// no element found
return false;
}
}
The complete code for the PascalSet class is included as a download with this article. Along with the class, there is an interactive WinForms testing application, SetTester, from which you can create a PascalSet instance and perform various set operations, viewing the resulting set.
Maintaining a Collection of Disjoint Sets
Next time you do a search at Google notice that with each result there's a link titled "Similar Pages." If you click this link, Google displays a list of URLs that are related to the item whose "Similar Pages" link you clicked. While I don't know how Google particularly determines how pages are related, one approach would be the following:
- Let x be the Web page we are interested in finding related pages for.
- Let S1 be the set of Web pages that x links to.
- Let S2 be the set of Web pages that the Web pages in S1 link to.
- Let S3 be the set of Web pages that the Web pages in S2 link to.
- …
- Let Sk be the set of Web pages that the Web pages in Sk-1 link to.
All of the Web pages in S1, S2, up to Sk are the related pages for x. Rather than compute the related Web pages on demand, we might opt to create the set of related pages for all Web pages once, and to store this relation in a database or some other permanent store. Then, when a user clicks on the "Similar Pages" link for a search term, we simply query the display to get the links related to this page.
Google has some sort of database with all of the Web pages it knows about. Each of these Web pages has a set of links. We can compute the set of related Web pages using the following algorithm:
- For each Web page in the database create a set, placing the single Web page in the set. (After this step completes, if we have n Web pages in the database, we'll have n one-element sets.)
- For a Web page x in the database, find all of those Web pages it directly links to. Call these linked-to pages S. For each element p in S, union the set containing p with x's set.
- Repeat step 2 for all Web pages in the database.
After step 3 completes, the Web pages in the database will be partitioned out into related groups. To view a graphical representation of this algorithm in action, consult Figure 1.

Figure 1. A graphical representation of an algorithm for grouping linked web pages.
Examining Figure 1, notice that in the end, there are three related partitions:
- w0
- w1, w2, w3, and w4
- w5 and w6
So, when a user clicks the "Similar Pages" link for w2, they would see links to w1, w3, and w4; clicking the "Similar Pages" link for w6 would show only a link to w6.
Notice that with this particular problem only one set operation is being performed—union. Furthermore, all of the Web pages fall into disjoint sets. Given an arbitrary number of sets, these sets are said to be disjoint if they share no elements in common. {1,2,3} and {4,5,6} are disjoint, for example, while {1,2,3} and {2,4,6} are not, since they share the common element {2}. In all stages shown in Figure 1, each of the sets containing Web pages are disjoint. That is, it's never the case that one Web page exists in more than one set at a time.
When working with disjoint sets in this manner, we often need to know what particular disjoint set a given element belongs to. To identify each set we arbitrarily pick a representative. A representative is an element from the disjoint set that uniquely identifies that entire disjoint set. With the notion of a representative, I can determine if two given elements are in the same set by checking to see if they have the same representative.
A disjoint set data structure needs to provide two methods:
- GetRepresentative(element) – this method accepts an element as an input parameter and returns the element's representative element.
- Union(element, element) – this method takes in two elements. If the elements are from the same disjoint set, then Union() does nothing. If, however, the two elements are from different disjoint sets, then Union() combines the two disjoint sets into one set.
The challenge that faces us now is how to efficiently maintain a number of disjoint sets, where these disjoint sets are often merged from two sets into one? There are two basic data structures that can be used to tackle this problem: one uses a series of linked lists, the other a collection of trees.
Maintaining Disjoint Sets with Linked Lists
In Part 4 of this article series we took a moment to look at a primer on linked lists. Recall that linked lists are a set of nodes that typically have a single reference to their next neighbor. Figure 2 shows a linked list with four elements.

Figure 2. A linked list with four elements
For the disjoint set data structure, a set is represented using a modified linked list. Rather than just having a reference to its neighbor, each node in the disjoint set linked list has a reference to the set's representative. As Figure 3 illustrates, all nodes in the linked list point to the same node as their representative, which is, by convention, the head of the linked list. (Figure 3 shows the linked list representation of the disjoint sets from the final stage of the algorithm dissected in Figure 1. Notice that for each disjoint set there exists a linked list, and the nodes of the linked list contain the elements of that particular disjoint set.)

Figure 3. A linked list representation of the disjoint sets from the final stage of the algorithm dissected in Figure 1.
Since each element in a set has a direct reference back to the set's representative, the GetRepresentative(element) method takes constant time. (To understand why, consider that regardless of how many elements a set has, it will always take one operation to find a given element's representative, since it involves just checking the element's representative reference.)
Using the linked list approach, combining two disjoint sets into one involves adding one linked list to the end of another, and updating the representative reference in each of the appended nodes. The process of joining two disjoint sets is depicted in Figure 4.

Figure 4. The process of joining two disjoint sets
When unioning together two disjoint sets, the correctness of the algorithm is not affected by which of the two sets is appended to the other. However, the running time can be. Imagine that our union algorithm randomly chose one of the two linked lists to be appended to the other. By a stroke of bad luck, imagine that we always chose the longer of the two linked lists to append. This can negatively impact the running time of the union operation since we have to enumerate all of the nodes in the appended linked list to update their representative reference. That is, imagine we make n disjoint sets, S1 to Sn. Each set would have one element. We could then do n - 1 unions, joining all n sets into one big set with n elements. Imagine the first union joined S1 and S2, having S1 be the representative for this two element unioned set. Since S2 only has one element, only one representative reference would need to be updated. Now, imagine S1—which has two elements—is unioned with S3, and S3 is made the representative. This time two representative references—S1's and S2's—will need to be updated. Similarly, when joining S3 with S4, if S4 is made the representative of the new set, three representative references will need to be updated (S1, S2, and S3). In the (n-1)th union, n-2 representative references will need to be updated.
Summing up the number of operations that must be done for each step, we find that the entire sequence of steps—n make set operations and n-1 unions—takes quadratic time—O(n2).
This worst-case running time can transpire because it is possible that union will choose the longer set to append to the shorter set. Appending the longer set requires that more nodes' representative references need to be updated. A better approach is to keep track of the size of each set, and then, when joining two sets, to append the smaller of the two linked lists. The running time when using this improved approach is reduced to O(n log2 n). A thorough time analysis is a bit beyond the scope of this article, and is omitted for brevity. Refer to the readings in the References section for a formal proof of the time analysis.
To appreciate the improvement of O(n log2 n) from O(n2), observe Figure 5, which shows the growth rate of n2 in blue, and the growth rate of n log2 n in pink. For small values of n, these two are comparable, but as n exceeds 32, the n log2 n grows much slower than n2. For example, performing 64 unions would require over 4,000 operations using the naïve linked list implementation, while it would take only 384 operations for the optimized linked list implementation. These differences become even more profound as n gets larger.

Figure 5. Growth rates of n2 and n log2
Maintaining Disjoint Sets with a Forest
Disjoint sets can also be maintained using a forest. A forest is a set of trees (get it? ). Recall that with the linked list implementation, the set's representative was the head of the list. With the forest implementation, each set is implemented as a tree, and the set's representative is the root of the tree. (If you are unfamiliar with what trees are, consider reading Part 3 of this article series, where we discussed trees, binary trees, and binary search trees.)
With the linked list approach, given an element, finding its set's representative was fast since each node had a direct reference to its representative. However, with the linked list approach unioning took longer because it involved appending one linked list to another, which required that the appended nodes' representative references be updated. The forest approach aims at making unions fast, at the expense of finding a set's representative given an element in the set.
The forest approach implements each disjoint set as a tree, with the root as the representative. To union together two sets, one tree is appended as a child of the other. Figure 6 illustrates this concept graphically.

Figure 6. The union of two sets
To union two sets together requires constant time, as only one node needs to have its representative reference updated. (In Figure 6, to union together the w1 and w3 sets, all we had to do was have w3 update its reference to w1—nodes w4 and w5 didn't need any modification.)
Compared to the linked list implementation, the forest approach has improved the time required for unioning two disjoint sets, but has worsened the time for finding the representative for a set. The only way we can determine a set's representative, given an element, is to walk up the set's tree until we find the root. Imagine that we wanted to find the representative for w5 (after sets w1 and w3 had been unioned). We'd walk up the tree until we reached the root—first to w3, and then to w1. Hence, finding the set's representative takes time relative to the depth of the tree, and not constant time as it does with the linked list representation.
The forest approach offers two optimizations that, when both employed, yield a linear running time for performing n disjoint set operations, meaning that each single operation has an average constant running time. These two optimizations are called union by rank and path compression. What we are trying to avoid with these two optimizations is having a sequence of unions generate a tall, skinny tree. As discussed in Part 3 of this article series, the ratio of a tree's height to breadth typically impacts its running time. Ideally, a tree is fanned out as much as possible, rather than being tall and narrow.
The Union by Rank Optimization
Union by rank is akin to the linked list's optimization of appending the shorter list to the longer one. Specifically, union by rank maintains a rank for each sets' root, which provides an upper-bound on the height of the tree. When unioning two sets, the set with the smaller rank is appended as a child of the root with the larger rank. Union by rank helps ensure that our trees will be broad. However, even with union by rank we might still end up with tall, albeit wide, trees. Figure 7 shows a picture of a tree that might be formed by a series of unions that adhere only to the union by rank optimization. The problem is that leaf nodes on the right hand side still must perform a number of operations to find their set's representative.

Figure 7. A tree that might be formed by a series of unions that adhere only to the union by rank optimization
Note The forest approach, when implementing just the union by rank optimization, has the same running time as the optimized link list implementation.
The Path Compression Optimization
Since a tall tree makes finding a set's representative expensive, ideally we'd like our trees to be broad and flat. The path compression optimization works to flatten out a tree. As we discussed earlier, whenever an element is queried for its set's representative, the algorithm walks up the tree to the root. The way the path compression optimization works is in this algorithm; the nodes that are visited in the walk up to the root have their parent reference updated to the root.
To understand how this flattening works, consider the tree in Figure 7. Now, imagine that we need to find the set representative for w13. The algorithm will start at w13, walk up to w12, then to w8, and finally to w1, returning w1 as the representative. Using path compression, this algorithm will also have the side effect of updating w13 and w12's parents to the root—w1. Figure 8 shows a screenshot of the tree after this path compression has occurred.

Figure 8. A tree after path compression
Path compression pays a slight overhead the first time when finding a representative, but benefits future representative lookups. That is, after this path compression has occurred, finding the set representative for w13 takes one step, since w13 is a child of the root. In Figure 7, prior to path compression, finding the representative for w13 would have taken three steps. The idea here is that you pay for the improvement once, and then benefit from the improvement each time the check is performed in the future.
When employing both the union by rank and path compression algorithms, the time it takes to perform n operations on disjoint sets is linear. That is, the forest approach, utilizing both optimizations, has a running time of O(n). You'll have to take my word on this, as the formal proof for the time complexity is quite lengthy and involved, and could easily fill several printed pages. If you are interested, though, in reading this multi-page time analysis, refer to the "Introduction to Algorithms" text listed in the references.
References
- Alur, Rajeev. "Disjoint Sets"
- Cormen, Thomas H., Charles E. Leiserson, and Ronald L. Rivest. "Introduction to Algorithms." MIT Press. 1990.
- Devroye, Luc. "Disjoint Set Structures".
Related Books
- Introduction to Algorithms by Thomas H. Cormen
Scott Mitchell, author of five books and founder of 4GuysFromRolla.com, has been working with Microsoft Web technologies for the past five years. Scott works as an independent consultant, trainer, and writer, and recently completed his Masters degree in Computer Science at the University of California, San Diego. He can be reached at mitchell@4guysfromrolla.com or through his blog at http://www.ScottOnWriting.NET.
























 2371
2371

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








