整理下最近回顾相似度计算的笔记
目录
一、欧式距离
欧式距离是最常见的一种距离度量方式,衡量的是多维空间中两个点之间的绝对距离。
计算公式如下:
1、n维空间中的点x和y的坐标分别为: ,
,则点x和点y之间的欧式距离为:

2、二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离:
3、两个n维向量和向量
之间的欧式距离为:

二、汉明距离
汉明距离(Hamming Distance)可以用来计算长度相等两个向量的相似度;
1、汉明距离的计算方式为:比较向量的每一位是否相同,若不同则汉明距离加1,这样即可得到汉明距离。向量相似度越高,对应的汉明距离越小。
2、汉明距离可以比较两个二进制串,a=11101010,b=11011010。a和b两个二进制串不同的位数为2,则汉明距离为2。
三、*余弦相似度*
余弦相似度:是利用两个向量之间的夹角的余弦值来衡量两个向量之间的余弦相似度。两个向量越相似夹角越小,余弦值越接近1。

1、a,b为两个向量,余弦距离计算公式为:

注:分子为向量a与向量b的内积,分母为向量a的模乘以向量b的模。
附录:向量模(即向量的长度)计算方法:

2、n维向量的余弦相似度计算。
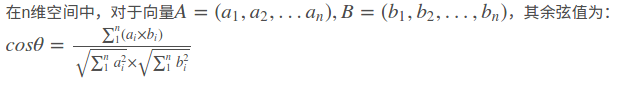
或详细写
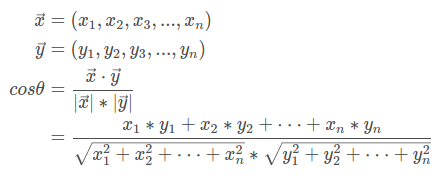
3、余弦相似度的取值范围为[-1,1],越接近于1表示相似度越高。
























 6997
6997

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








