基于实例的学习方法中,K-近邻算法算是最基本的了。K-近邻算法嘉定所有实例对应与n维空间中的点,一个实例的最近邻是根据标准欧氏距离定义的。
例如把x表示为一个特征向量:
< a1(x), a2(x), a3(x), ...an(x) >其中,ar(x)表示实例x的第r个属性值,所以xi和xj的间距定义为d(xi, xj),其中:
以上就是距离的公式定义。®
目标函数值可以是离散的,也可以是实值。
下面是机器学习书上的,逼近离散目标函数的k-近邻算法。
上面所写的,返回函数是一个估计值,就是距离xq最近的k个训练样例中最普通的f值。如果我们选择k=1,那么"1邻近算法"就是把最靠近xi的xq当做训练实例。对于较大的k值,这个算法返回前k个最靠近的训练实例中最普遍得值。
上面的流程是二维空间中的点,目标函数也是布尔值。
加权最近邻算法
对k-近邻算法的改进,有一个很明显的办法,就是:
对k个近邻的贡献进行加权。
根据他们相对查询点xq的距离,将较大的权值赋值给较近的近邻。流程不变,还是如上面图片中的流程,不过对于每个近邻与xq的距离平方倒数加权这个近邻的『选举权』。公式如下:
这里可以看到,就是多了一个omega i,这个就是加权值。
这里为了防止xq和xi刚好相等,导致d(xq,xi)为0的情况,可以认为出现这种情况,结果直接为f(xi),如果是多个这样的训练阳历,那就就使用他们占多数的分类。
也可以用类似的方式对实值目标函数进行距离加权,用一下公式替换:
这里可以发现,上面的分母是个常量,把不同权值的贡献归一化。
以上的近邻算法的所有遍体都只考虑k个近邻用来分类查询点。如果使用按距离加权,那么允许所有的训练阳历影响xq的分类事实上没有坏处,因为非常远的实例对结果的影响很小,考虑所有样例的唯一不足是会使分类运行的更慢。如果分类一个新的查询实例时考虑所有的样例训练,我们称之为全局法。如果仅仅考虑最近的训练样例,我们称之为局部法。
对k-近邻算法说明
按照距离加权的K-近邻算法是一种很有效的归纳推理方法。对训练数据的噪声有很好的健壮性,而且当给定足够大的训练集的时候,也非常有效。取k个近邻加权平均,可以消除孤立的噪声样例的影响
k近邻算法的归纳偏置对应于假定:
一个实例的分类
xq与在欧式空间中它附近的实例的分类相似。
维度灾难
应用k-近邻算法的一个实践问题是,实例间的距离是根据实例的所有属性计算的。这与那些只选择全部实例属性的一个子集方法不同,例如决策树学习系统。 如果每个实例由20个属性描述,但是这些属性中仅仅2个属性与它的分类有关,这种情况,两个相关属性一致的实例可能在这个20维空间实例中相距很远,结果就是这些不相关属性会导致近邻间距离被支配。这种由于存在很多不相关属性所导致的难题,有时被称为维度灾难。
解决方法
- 解决方法也比较简单,就是计算距离的时候,对属性加权。这样就会减小不相关属性的影响。
- 另一种方法是:从实例空间中完全消除最不相关属性,等效认为是对某个属性设置缩放因子为0。
建立高效索引
因为这个算法推迟所有的处理,知道接收到一个新的查询,所以每个新查询都可能需要大量的计算。目前有的方法:
1. kd-tree (Bentley 1975; Friedman et al. 1977),把实例存储在树叶节点内,邻近的实例存储在同一个或附近的节点内。
以上是KNN的大致内容。








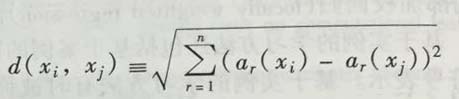

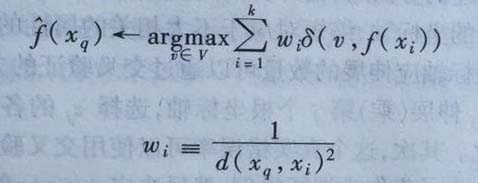
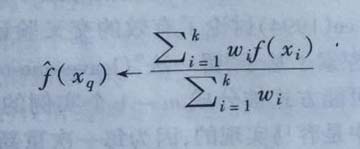
















 2575
2575

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








