Python实现逐步回归

@创建于：2023.09.17
@修改于：2023.09.17

本文转自阿黎逸阳的Python实现逐步回归，
纯属为了记录，不做任何商用。

Python实现逐步回归

逐步回归（Stepwise Regression）是一种逐步选择变量的回归方法，用于确定最佳的预测模型。它通过逐步添加和删除变量来优化模型的预测能力。

本文重点讲解什么是逐步回归，以及用Python如何实现逐步回归。

1 什么是逐步回归？

逐步回归是回归分析中一种筛选变量的过程，我们可以使用逐步回归从一组候选变量中筛选起作用的变量或剔除不起作用的变量进而构建模型。

逐步回归有三种筛选变量的方法。

1. 向前筛选（forward selection）: 首先挑选单独解释因变量变异最大的自变量，然后将剩余自变量逐个引入模型，引入后看该变量的加入是否使得模型发生显著性变化（F检验），如果发生了显著性变化，则将该变量引入模型中，否则忽略该变量，直至所有变量都进行了考虑。

特点：自变量一旦选入，则永远保存在模型中。

2. 向后筛选（Backward elimination）: 与向前筛选相反，一开始就把所有变量放入模型，然后尝试将某一变量进行剔除，查看剔除后对整个模型是否有显著性变化（F检验），如果没有显著性变化则剔除，若有则保留，直到留下所有对模型有显著性变化的因素。

特点：自变量一旦剔除，则不再进入模型，且一开始把全部自变量引入模型，计算量过大。

3. 双向筛选（Bidirectional elimination）: 这种方法相当于前两种筛选方法的结合。当引入一个变量后，首先查看这个变量是否使得模型发生显著性变化（F检验），若发生显著性变化，再对所有变量进行t检验，当原来引入变量由于后面加入的变量的引入而不再显著变化时，则剔除此变量，确保每次引入新的变量之前回归方程中只包含显著性变量，直到既没有显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止，最终得到一个最优的变量集合。

2 实现逐步回归的函数参数详解

实现逐步回归，可以使用toad库中的toad.selection.stepwise函数，该函数的调用方法、主要参数及其解释如下：

import toad 

toad.selection.stepwise(frame, target='target', estimator='ols', direction='both', criterion='aic', p_enter=0.01, p_remove=0.01, p_value_enter=0.2, intercept=False, max_iter=None, return_drop=False, exclude=None)

frame：输入数据框，包含自变量和目标变量。
target：指定目标变量在数据框中的列名，默认是target，可根据实际情况调整。
estimator： 用于拟合的模型，支持’ols’（默认项）、‘lr’、‘lasso’、‘ridge’。
direction：逐步回归的方向，支持’forward’（向前法）、 ‘backward’（向后法）、‘both’ （双向法，默认项）。
criterion：指定选择特征的准则，可以为’aic’（赤池信息准则，默认项）、‘bic’（贝叶斯信息准则）、 ‘ks’、 ‘auc’。
p_enter：指定添加特征的显著性水平，默认为0.01。
p_remove: 指定删除特征的显著性水平，默认为0.01。
p_value_enter: 指定添加特征的P值阈值，默认为0.2。
intercept: 是否拟合截距项，默认为False。
max_iter: 指定最大迭代次数，默认为None，即不限制迭代次数。
return_drop: 是否返回被删除的特征名，默认为False。
exclude: 指定要排除训练的特征列名列表，比如ID列和时间列，默认为None。

经验说：

1. direction = ‘both’效果一般最好。
2. estimator = ‘ols’以及criterion = ‘aic’运行速度快且结果对逻辑回归建模有较好的代表性。

以上2点是平常的经验总结，具体还是需要根据建模的数据进行具体的分析。

3 Python实现逐步回归

3.1 读取数据

首先导入建模数据，进行数据预处理。由于本文的重点是逐步回归实现，且之前的文章企业欺诈识别已对该模块进行了详细阐述，本文不再赘述。
具体代码如下：

import os
import toad
import numpy as np
import pandas as pd

os.chdir(r'F:\公众号\3.企业欺诈识别\audit_data')  #设置数据读取的文件夹
qz_date = pd.read_csv('audit_risk.csv')           #读取数据
qz_date.LOCATION_ID = pd.to_numeric(qz_date.LOCATION_ID, errors = 'coerce')  #把文本数据转换成数值型数据
qz_date = qz_date.fillna(0)                       #用0填充数据框中的空值
qz_date.head(5)

得到结果：

可以发现此数据包含27列。

3.2 双向筛选逐步回归实现

接着用双向筛选的方法进行逐步回归变量挑选，具体代码如下：

final_data = toad.selection.stepwise(qz_date,
                                    target = 'Risk',
                                     estimator='ols', 
                                     direction = 'both', 
                                     criterion = 'aic'
                                     )
final_data

得到结果：

可以发现双向逐步回归挑选出了12个入模变量。

3.3 向前筛选逐步回归实现

接着用向前筛选的方法进行逐步回归变量挑选，具体代码如下：

final_data = toad.selection.stepwise(qz_date,
                                    target = 'Risk',
                                     estimator='ols', 
                                     direction = 'forward', 
                                     criterion = 'aic'
                                     )
final_data

得到结果：

可以发现向前逐步回归挑选出了13个入模变量，比双向逐步回归多入模了RiSk_E变量，其余变量一致。

3.4 向后筛选逐步回归实现

接着用向后筛选的方法进行逐步回归变量挑选，具体代码如下：

final_data = toad.selection.stepwise(qz_date,
                                    target = 'Risk',
                                     estimator='ols', 
                                     direction = 'backward', 
                                     criterion = 'aic'
                                     )
final_data

得到结果：

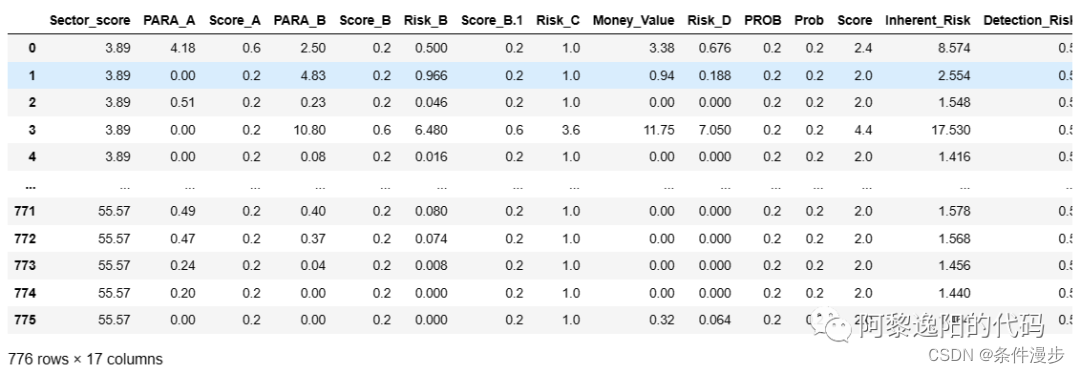
可以发现向后逐步回归挑选出了16个入模变量，和双向、向前逐步回归都有一定的区别。

3.5 双向逐步回归指定特征筛选准则为ks

为了分析不同特征选择准则对变量筛选的影响，接着在双向逐步回归时指定特征选择准则为ks，看下结果，具体代码如下：

final_data = toad.selection.stepwise(qz_date,
                                    target = 'Risk',
                                     estimator='ols', 
                                     direction = 'both', 
                                     criterion = 'ks'
                                     )
final_data

得到结果：

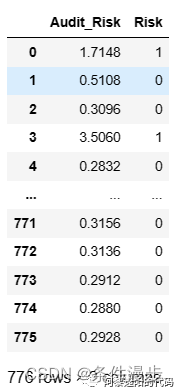
可以发现双向逐步回归时如果特征选择准则设定为ks，只挑选出了1个入模变量，明显不太符合建模的要求。

3.6 双向逐步回归指定特征筛选准则为auc

接着在双向逐步回归时指定特征选择准则为auc，具体代码如下：

final_data = toad.selection.stepwise(qz_date,
                                    target = 'Risk',
                                     estimator='ols', 
                                     direction = 'both', 
                                     criterion = 'auc'
                                     )
final_data

得到结果：

可以发现双向逐步回归时如果特征选择准则设定为auc，也只挑选出了1个入模变量,明显不太符合建模的要求。

综上，我们在用逐步回归建模时可以参考之前的经验参数。

参考资料

Python实现逐步回归