二叉树

一、二叉树的前序遍历

1、前序遍历递归解法规则

① 如果二叉树为空，空操作返回；② 如果二叉树不为空，访问根节点，前序遍历左子树，前序遍历右子树。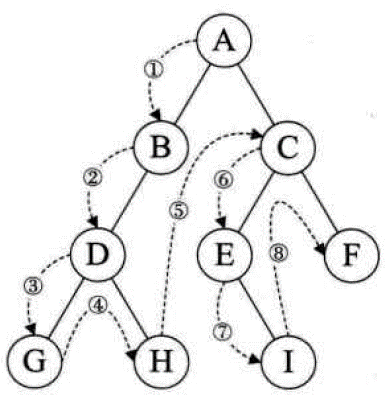

参考代码：

	/**
	 * 前序遍历—递归方式
	 */
	public void preOrderTraverse(TreeNode node) {
		if (node == null) {
			return;
		} else {
			//访问根节点
			System.out.println("preOrder data:" + node.getData());
			//前序遍历左子树
			preOrderTraverse(node.leftChild);
			//前序遍历右子树
			preOrderTraverse(node.rightChild);
		}
	}

2、前序遍历非递归解法规则

① 如果二叉树为空，则空操作返回；② 新建一个栈，将传入的节点入栈；③ 循环遍历栈是否为空，如果不为空，首先弹出节点并访问节点中存储的数据；然后判断节点的右孩子是否为空，如果不为空则将右孩子入栈；最后判断节点的左孩子是否为空，如果不为空则将左孩子入栈。
参考代码：

	/**
	 * 前序遍历—非递归方式
	 */
	public void preOrder(TreeNode node) {
		//如果二叉树为空，则返回
		if (node == null) {
			return;
		}

		//新建一个栈，并将节点入栈
		Stack<TreeNode> stack = new Stack<TreeNode>();
		stack.push(node);

		//循环遍历栈中节点是否为空
		while (!stack.isEmpty()) {
			//弹出节点，并访问节点中存储的数据
			TreeNode popNode = stack.pop();
			System.out.println("popNode data:" + popNode.getData());

			//判断节点的右孩子是否存在，如果存在则入栈
			if (popNode.rightChild != null) {
				stack.push(popNode.rightChild);
			}

			//判断节点的左孩子是否存在，如果存在则入栈
			if (popNode.leftChild != null) {
				stack.push(popNode.leftChild);
			}
		}
	}

---

二、二叉树的中序遍历

1、中序遍历递归解法规则

① 如果二叉树为空，空操作返回；② 如果二叉树不为空，中序遍历左子树，访问根节点，中序遍历右子树。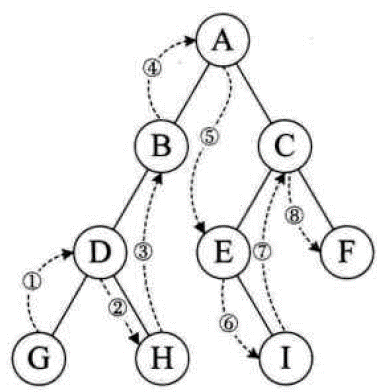

参考代码：

	/**
	 * 中序遍历—递归方式
	 */
	public void midOrderTraverse(TreeNode node) {
		if (node == null) {
			return;
		} else {
			// 中序遍历左孩子
			midOrderTraverse(node.leftChild);
			// 访问根节点
			System.out.println("midOrder data:" + node.getData());
			// 中序遍历右孩子
			midOrderTraverse(node.rightChild);
		}
	}

2、中序遍历非递归解法规则

① 如果二叉树为空，空操作返回；② 新建一个空栈；③ while循环中判断节点或则栈是否为空；④ while循环中判断节点是否为空，如果不为空则入栈该节点，并将节点指向节点的左孩子；⑤ 判断栈是否为空，如果栈不为空，首先出栈一个节点并访问该节点的数据域，然后将节点指向该节点的右孩子。
参考代码：

	/**
	 * 中序遍历—非递归方式
	 */
	public void midOrder(TreeNode node) {
		// 如果二叉树为空，怎返回
		if (node == null) {
			return;
		}
		// 新建一个栈
		Stack<TreeNode> stack = new Stack<TreeNode>();
		while (node != null || !stack.isEmpty()) {
			// 如果节点不为空，则循环入栈节点的左孩子
			while (node != null) {
				stack.push(node);
				node = node.leftChild;
			}

			if (!stack.isEmpty()) {
				// 如果栈不为空，出栈一个节点
				node = stack.pop();
				// 访问出栈节点的数据
				System.out.println("popNode data:" + node.getData());
				// 拿到节点的右孩子
				node = node.rightChild;
			}
		}
	}

---

三、二叉树的后序遍历

1、后序遍历递归解法规则

① 如果二叉树为空，空操作返回；② 如果二叉树不为空，后序遍历左子树，后序遍历右子树，访问根节点。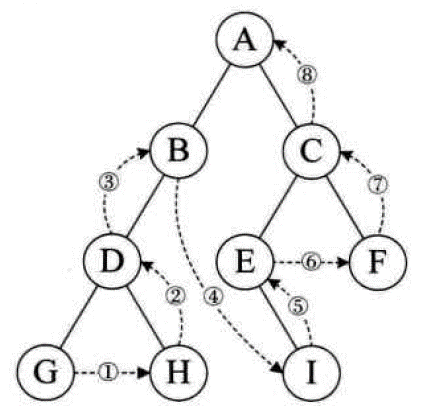

参考代码：

	/**
	 * 后序遍历—递归方式
	 */
	public void postOrderTraverse(TreeNode node) {
		if (node == null) {
			return;
		} else {
			// 后序遍历左孩子
			postOrderTraverse(node.leftChild);
			// 后序遍历右孩子
			postOrderTraverse(node.rightChild);
			// 访问根节点
			System.out.println("postOrder data:" + node.getData());
		}
	}

2、后序遍历非递归解法规则

① 如果二叉树为空，空操作返回；② 新建一个空栈，并入栈传入的节点；③ while循环判断栈是否为空；④ 在循环中判断当前节点如果没有孩子结点或者孩子节点都已被访问过 ，则访问该节点的值并弹出该节点，否则将该节点的孩子节点入栈。
参考代码：

	/**
	 * 后序遍历—非递归方式
	 */
	public void postOrder(TreeNode node) {
		// 如果二叉树为空，则返回
		if (node == null) {
			return;
		}

		// 新建一个空战 ，并入栈传入的节点
		Stack<TreeNode> stack = new Stack<TreeNode>();
		stack.push(node);
		// 当前访问的节点
		TreeNode curNode = null;
		// 前一次访问的结点
		TreeNode preNode = null;
		while (!stack.isEmpty()) {
			// 从栈中拿到当前节点，不能用pop弹出节点
			curNode = stack.peek();
			// 如果当前结点没有孩子结点或者孩子节点都已被访问过，则访问拿到的当前节点的数据，然后将preNode指针指向当前节点，最后pop弹出这个节点
			if ((curNode.leftChild == null && curNode.rightChild == null)
					|| (preNode != null && (preNode == curNode.leftChild || preNode == curNode.rightChild))) {
				System.out.println("popNode data:" + curNode.getData());
				preNode = curNode;
				stack.pop();
			} else {
				// 如果拿到的当前节点有孩子节点且没有被访问过，则入栈该节点
				if (curNode.rightChild != null) {
					stack.push(curNode.rightChild);
				}

				if (curNode.leftChild != null) {
					stack.push(curNode.leftChild);
				}
			}
		}
	}

---

四、求二叉树的节点个数

① 如果二叉树为空，节点个数为0；② 如果二叉树不为空，二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1
参考代码：

	/**
	 * 获取二叉树的节点个数
	 */
	public int getNodeNum(TreeNode root) {
		if (root == null) {
			return 0;
		} else {
			return 1 + getNodeNum(root.leftChild) + getNodeNum(root.rightChild);
		}
	}

---

五、求二叉树的深度

① 如果二叉树为空，二叉树的深度为0；② 如果二叉树不为空，二叉树的深度 = max(左子树深度， 右子树深度) + 1

	/**
	 * 获取二叉树的高度
	 */
	public int getTreeHeight(TreeNode root) {
		if (root == null) {
			return 0;
		} else {
			int depthLeft = getTreeHeight(root.leftChild);
			int depthRight = getTreeHeight(root.rightChild);
			return depthLeft > depthRight ? (depthLeft + 1) : (depthRight + 1);
		}
	}

---

本篇文章主要通过递归和非递归两种方式实现了二叉树的前序遍历、中序遍历、后序遍历，因为二叉树的遍历是一个很重要的知识点。
参考文章：轻松搞定面试中的二叉树题目

转载于:https://my.oschina.net/devbird/blog/832009