Leetcode279: 完全平方数(medium, BFS)_leetcode 279 bfs-CSDN博客

本文链接：https://blog.csdn.net/chenxy_bwave/article/details/120335807

1. 问题描述

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数（可以重复）的个数最少。给你一个整数 n ，返回和为 n 的完全平方数的最少数量。

完全平方数是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12，输出：3

解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13，输出：2

解释：13 = 4 + 9

提示：1 <= n <= 10^4

2. 解题分析

本题可以转化为图搜索中的最短路径问题，因此可以用广度优先搜索算法来解决。

举个例子，令n = 30, m=floor(sqrt(n)) = 5. 则构造n的完全平方数的和，可以使用模块（即数字）为1~5。从中任选一个k使用得到(n=30)的邻节点(n-k*k)。针对每个节点都执行同样操作，直到最后到达值为0的节点。如下图所示：

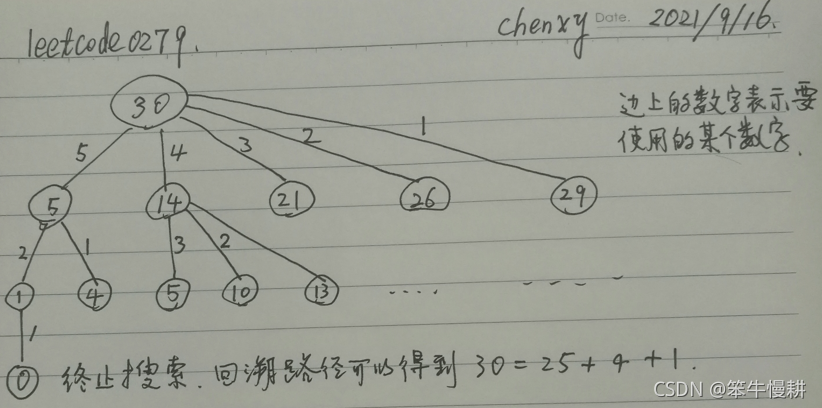
Edge上的数字表示要用于构成完全平方数和的数（其实是其平方），对应的子节点的值等于父节点的值减去该数的平方。

广度优先搜索的三个基本要素：

队列管理
节点的表示以及邻节点的遍历
已访问节点的管理

在本问题中，邻节点即从当前节点出发，将每个可用的数（的平方）用一次（即减去）后能到达的下一个值。可以以递推关系式表示如下：

3. 代码及测试

import sys
import time
import datetime
import math
import random
from   typing import List
# from   queue import Queue
from   collections import deque
import itertools as it
from   math import sqrt, floor, ceil
import numpy 

class Solution:

    def numSquares_bfs_set(self, n: int) -> int:
        queue = deque()
        queue.append((n,0))
        visited = set([n])
        
        while queue:
            vertex = queue.popleft()
            for k in range(1,floor(sqrt(vertex[0])+1)):
                nxtNum = vertex[0] - k*k           
                if nxtNum==0:                   
                    return vertex[1]+1
                    
                elif nxtNum not in visited:
                    queue.append((nxtNum,vertex[1]+1))
                    visited.add(nxtNum)
                                        
        return -1

if __name__ == '__main__':        
    
    sln = Solution()
    
    # n = 4696
    n = 9999

    tStart = time.time()
    nums = sln.numSquares_bfs_set(n)
    tCost = time.time() - tStart
    print('numSquares_bfs_set({0}) = {1}, tCost = {2}(sec)'.format(n,nums,tCost))

函数最后返回"-1" ，其实意思是正常不应该到到达这里。到达这里意味着程序存在错误。

另外需要注意的是，deque是双向队列，它的append()是和popleft()相对应的。另一对对应的方法是appendleft()和pop()。

提交结果：

4. 后记

(1) 本题一开始提交超时失败了。原因查明了是因为使用list来实现visited，是python list用于查询的性能太差导致超时了。改用set实现后就OK。比较了一下，用set实现的查询效率比list实现的查询效率毛估估高两个数量级。另外，还可以用dict来实现visited，dict的查询效率与set相当。后面有时间要做一次三者的查询效率对比实验。

(2) 如第2节中的递推表达式所示，本题也可以用动态规划的策略来解决。而且有不止一种递推关系。这个后面再来补课。