皮尔逊相关系数的5个假设

目录

 

1. 概要

2. 假设1：度量类别

3. 假设2：线性关系

4. 假设3：正态性

4.1 直方图，Histogram

4.2 Q-Q plot

 4.3 定量的统计测试

5. 假设4：关联数据对

6. 假设5：没有异常值

---

1. 概要

        皮尔逊相关系数(Pearson correlation coefficient: also known as the “product-moment correlation coefficient”)衡量两个变量之间的线性关联度(linear association).

        皮尔逊相关系数取值在1与-1之间：

• -1 表示完全负相关，比如说，y=-kx
• 0 表示两个变量之间没有线性关系
• 1 表示完全正相关，比如说，y=kx

 

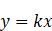
        然而，当我们计算两个随机变量之间的皮尔逊相关系数时，我们假定了它们满足以下5个假设:

1. Level of Measurement: The two variables should be measured at the interval or ratio level.

2. Linear Relationship: There should exist a linear relationship between the two variables.

3. Normality: Both variables should be roughly normally distributed.

4. Related Pairs: Each observation in the dataset should have a pair of values.

5. No Outliers: There should be no extreme outliers in the dataset.

        以下各章我们分别介绍每个假设以及如何判断各假设条件是否满足

 

2. 假设1：度量类别

        计算两个变量之间的皮尔逊相关系数，要求两个变量同是以等距尺度或者同是以等比尺度进行测量的。

        根据百度百科的解释，测量尺度（scale of measure）或称度量水平（level of measurement）、度量类别（个人感觉“度量类别”是最合适的中文词汇，其它两个都容易引起误解），是统计学和定量研究中，对不同种类的数据，依据其尺度水平所划分的类别，这些尺度水平分别为：名目（nominal）、次序（ordinal）、等距（interval）、等比（ratio）。

        名目尺度和次序尺度是定性的，而等距尺度和等比尺度是定量的。定量数据，又根据数据是否可数，分为离散的和连续的。

       关于度量类别的简要解释参见以下两表：

 

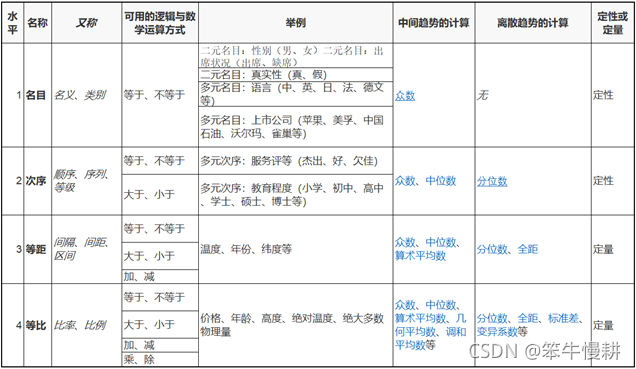
        这里要注意等距尺度与等比尺度的一些量很容易混淆。等比尺度度量量相比等距尺度度量量多了一个基准参考量（即第一张表中的所谓的“true zero” value），因此可以计算两个测量量之间的比例关系，因此在“可用的逻辑与数学运算方式”中多了乘和除两个运算。比方说，在我们日常生活中，当我们说温度和年份时，我们不会说2000年时1000年的两倍，也不会说40度是20度的两倍。但是当谈起价格或年龄时，就可以说比如30岁的人的年龄是10岁小孩的3倍了。

 

        顺便提一下，对于次序度量(ordinal level)的两个变量，要采用斯皮尔曼相关系数来度量它们之间的相关性。参见：斯皮尔曼相关系数介绍及其计算例https://blog.csdn.net/chenxy_bwave/article/details/121427036https://blog.csdn.net/chenxy_bwave/article/details/121427036

 

3. 假设2：线性关系

 

        皮尔逊相关系数是用于衡量两个变量之间的线性关系（线性相关度）的，所以自然是要求两个变量之间本来是存在线性关系的。

        画出两个变量数据之间的散点图（scatter plot），如下图所示，就可以大致判断它们之间是否存在线性关系。

      下面这个图表明x和y之间是存在明显的线性关系的。

        但是下面这两个图就表明两者之间显然不是线性关系，左图更像是平方关系（quadratic），而右图则表明两者之间可能没有啥关系（不相关）: 

        【问题】在两个变量之间不存在线性关系时，进行皮尔逊相关系数估计会得到什么结果呢？ 

 

4. 假设3：正态性

        皮尔逊相关系数假设两个变量都是近似于正态分布。可以通过画直方图或者Q-Q plot来直观地检查各个变量是否近似于正太分布。

 

4.1 直方图，Histogram

        如果一个数据集合的直方图大体上呈钟形曲线的话，基本上就可以认为它近似于正态分布。可以利用各种软件包中的相关工具函数在做直方图时顺便给出拟合曲线，这样就可以更直观地看出与正态分布有多高的契合度，如下图所示。

4.2 Q-Q plot

        Q-Q是“quantile-quantile”的缩写。Quantile的意思是‘分位数，分位点’，它用于描绘假定是正态分布时对应于x值的分位数理论值与实际样本的分位数之间的对比。显然，如果样本数据是近似于正态分布的话，那Q-Q图就应该近似于y=x的直线。

        下图为一个Q-Q图的示例（显示该数据样本是基本符合正态分布的）。

 4.3 定量的统计测试

        以上直方图和Q-Q图都只能定性地目测样本数据的正态性。也可以进行定量的统计测试以确定样本数据的正态性。有以下三种统计方法用于测试样本数据的正态性(具体实施方法就不在本文中详细描述了)。

1. Jarque-Bera Test
2. Shapiro-Wilk Test
3. Kolmogorov-Smirnov Test

        如果测试所得的p值小于一个某预定的显著水平(significance level, 比如说a=0.05)，那就有充分的信心相信待测数据样本集不符合正态分布。

 

5. 假设4：关联数据对

        作为一个直观的理解，其实就是要求两个待测变量的数据样本必须是一一对应的。比如说，你要计算身高和体重的相关性的话，那对应于每个身高的测量数据必须有一个对应的体重测量数据，而且这种一一对应关系是确定性的。更具体一点说，每一对身高数据和体重数据必须是属于同一人的。比如说不能随机地打乱待测数据的顺序再进行相关系数计算，这样计算出来的相关系数是没有意义的。

 

6. 假设5：没有异常值

        皮尔逊相关系数对于异常值非常敏感，因此如果数据样本集中存在极端的异常值的话，会导致皮尔逊相关系数估计失去其可信度。所以在进行皮尔逊相关系数之前需要检查是否存在异常值，并进行响应的异常值去除处理。

        下面我们举一个例子来展示异常值对于皮尔逊相关系数的影响。考虑以下这个数据集，计算X与Y之间的皮尔逊相关系数可以得到0.949。

        但是如果我们把其中某个Y值更改一下，比如说把X=19对应的Y值更改为105，重新计算X与Y之间的皮尔逊相关系数得到的是0.711。仅仅一个极端异常值就严重影响了两个变量之间的皮尔逊相关系数值。由此可见，在进行皮尔逊相关系数计算之前检查并去除异常值的意义之所在。 

 

[Reference]

[1] The Five Assumptions for Pearson Correlation - Statology

[2] 百度百科——全球领先的中文百科全书测量尺度

 

相关文章：

(8条消息) 皮尔逊相关(Pearson correlation)系数概述及其计算例_笨牛慢耕的博客-CSDN博客_pearson系数https://chenxiaoyuan.blog.csdn.net/article/details/121576303

斯皮尔曼相关系数(Spearman correlation coefficient)介绍及其计算例https://blog.csdn.net/chenxy_bwave/article/detailshttps://blog.csdn.net/chenxy_bwave/article/details