Exp1 Theory: Shamir Secret Sharing

最早在1970年基于Lagrange插值和矢量方法提出。基本思想是分发者通过秘密多项式,将秘密s分解为n份毫无相关的部分信息,每一部分信息称为一个子密钥,由一个参与者持有。只有至少拥有t份子密钥时才能恢复出秘密s,任意少于t个秘密均无法得到密文的任何信息。这种方案称为(t, n)-秘密分割门限方案,t称为方案的门限值。(可以根据已知位于曲线上的 t 或更多点的知识重构 t-1 次多项式)
算法思路
1.加密过程
-
假设存在秘密S,任取t-1个随机数 ( a 1 , a 2 , . . . , a t − 1 ) (a_1,a_2,...,a_{t-1}) (a1,a2,...,at−1),构造多项式:
f ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a t − 1 x t − 1 [ m o d ( p ) ] f(x)=a_0+a_1x+a_2x^2+...+a_{t-1}x^{t-1} [mod(p)] f(x)=a0+a1x+a2x2+...+at−1xt−1[mod(p)]
其中 a 0 = S a_0=S a0=S,所有运算均在有有限域(仅含有限个元素的域)中进行。
-
任取n个数 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn,分别代入多项式,计算 y i = f ( x i ) y_i=f(x_i) yi=f(xi)。
-
将n个密钥对 ( x 1 , f ( x 1 ) ) , ( x 2 , f ( x 2 ) ) , . . . , ( x n , f ( x n ) ) (x_1,f(x_1)),(x_2,f(x_2)),...,(x_n,f(x_n)) (x1,f(x1)),(x2,f(x2)),...,(xn,f(xn))分发给n个持有者。
2.解密过程
任取t个密钥对,代入并求解多项式系数:
a 0 + a 1 x 1 + . . . + a t − 1 x 1 t − 1 = y 1 a 0 + a 1 x 2 + . . . + a t − 1 x 2 t − 1 = y 2 . . . a 0 + a 1 x t + . . . + a t − 1 x t t − 1 = y t a_0+a_1x_1+...+a_{t-1}x_1^{t-1}=y_1 \\ a_0+a_1x_2+...+a_{t-1}x_2^{t-1}=y_2 \\ ... \\ a_0+a_1x_t+...+a_{t-1}x_t^{t-1}=y_t a0+a1x1+...+at−1x1t−1=y1a0+a1x2+...+at−1x2t−1=y2...a0+a1xt+...+at−1xtt−1=yt
- 解法一:用矩阵乘法表示为:
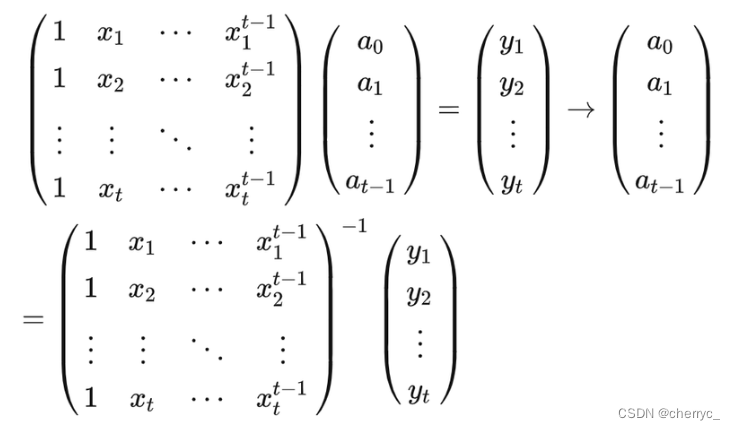
在求得 a 0 , a 1 , . . . , a t − 1 a_0,a_1,...,a_{t-1} a0,a1,...,at−1后便可构造出多项式。
将 x = 0 x=0 x=0代入多项式,即可求得原秘密。
-
解法二:拉格朗日插值法:
解密结果为:
f ( x ) = ∑ i = 1 t y i ∏ j = 1 , j ≠ i t x − x j x i − x j f\left( x \right) =\sum_{i=1}^t{y_i\prod_{j=1,j\ne i}^t{\frac{x-x_j}{x_i-x_j}}} f(x)=i=1∑tyij=1,j=i∏txi−xjx−xj
令 x = 0 x=0 x=0,解得秘密S:
s = ∑ i = 1 t y i ∏ j = 1 , j ≠ i t x j x j − x i s=\sum_{i=1}^t{y_i\prod_{j=1,j\ne i}^t{\frac{x_j}{x_j-x_i}}} s=i=1∑tyij=1,j=i∏txj−xixj
💡 对某个多项式函数,已知有给定的k+1个取值点: ( x 0 , y 0 ) , . . . , ( x k , y k ) (x_0,y_0),...,(x_k,y_k) (x0,y0),...,(xk,yk),其中对应着自变量的位置,对应函数在这个位置的取值,任意两个都不相同。那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为:
L ( x ) = ∑ j = 0 k y j l j ( x ) L\left( x \right) =\sum_{j=0}^k{y_jl_j\left( x \right)} L(x)=j=0∑kyjlj(x)
其中每个为拉格朗日基本多项式(或称插值基函数)
l j ( x ) = ∏ i = 0 , i ≠ j k x − x i x j − x i l_j\left( x \right) =\prod_{i=0,i\ne j}^k{\frac{x-x_i}{x_j-x_i}} lj(x)=i=0,i=j∏kxj−xix−xi
即
l j ( x ) = { 0 , x ≠ x j ( 总会有 x = x i ) 1 , x = x j l_j\left( x \right) =\left\{ \begin{array}{l} 0,\ x\ne x_j(总会有x=x_i)\\ 1,\ x=x_j\\\end{array} \right. lj(x)={0, x=xj(总会有x=xi)1, x=xj
简化推理:
已知一个三次多项式上的4个点,构造多项式。




👆这是一个三次多项式,几个 δ ( x ) \delta(x) δ(x)相加后得到的 f ( x ) f(x) f(x)仍是三次多项式。将 δ ( x ) \delta(x) δ(x)泛化为以下表达式:
将 f ( x ) f(x) f(x)泛化为以下表达式:
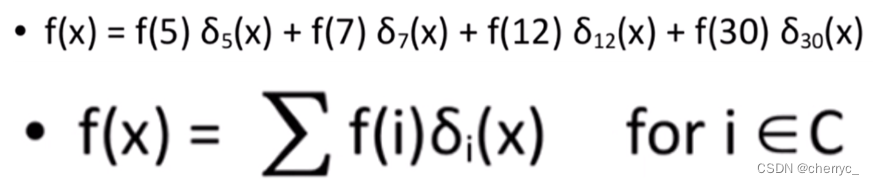
3.拓展:同态性质
(1)加法同态
多个(t, n) Shamir秘密共享生成的秘密份额相加是对应秘密值和的秘密份额,并且此过程中的门限值始终为t。即t个对应秘密值和的秘密份额可以恢复对应秘密值之和。
人话:

使用拉格朗日插值法计算公式与计算单个秘密值的形式相同。
(2)乘法同态
如果d个(t,n)-Shamir分享多个秘密值,那么这若干个f1,f2…fd乘起来最高次就是d(t-1),加上常数项,共有d(t-1) + 1 个未知数。因此如果d(t-1) + 1 > n,显然n个人全部一起来都无法恢复,所以必须要满足d(t-1) + 1 <= n才有可能恢复秘密值的乘积。也就是说Shamir秘密分享有d阶乘法同态性必须满足上述不等式。









 本文介绍了Shamir算法的基本原理,包括秘密多项式的分解、加密过程(利用随机数和有限域操作)以及解密方法(矩阵乘法或拉格朗日插值)。同时讨论了算法的加法和乘法同态性质。
本文介绍了Shamir算法的基本原理,包括秘密多项式的分解、加密过程(利用随机数和有限域操作)以及解密方法(矩阵乘法或拉格朗日插值)。同时讨论了算法的加法和乘法同态性质。

















 82
82

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








