分治法：递归及非递归实现循环赛日程安排问题（C++）

1、问题：
设有n=2^k个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表：
1、每个选手必须与其他n-1个选手各赛一次；
2、每个选手一天只能参赛一次；
3、循环赛在n-1天内结束。
按此要求，可将比赛日程表设计成一个n 行n-1列的二维表，在表中的第i行，第j列处填入第i个选手在第j天所遇到的选手。其中1≤i≤n，1≤j≤n-1。
2、问题分析
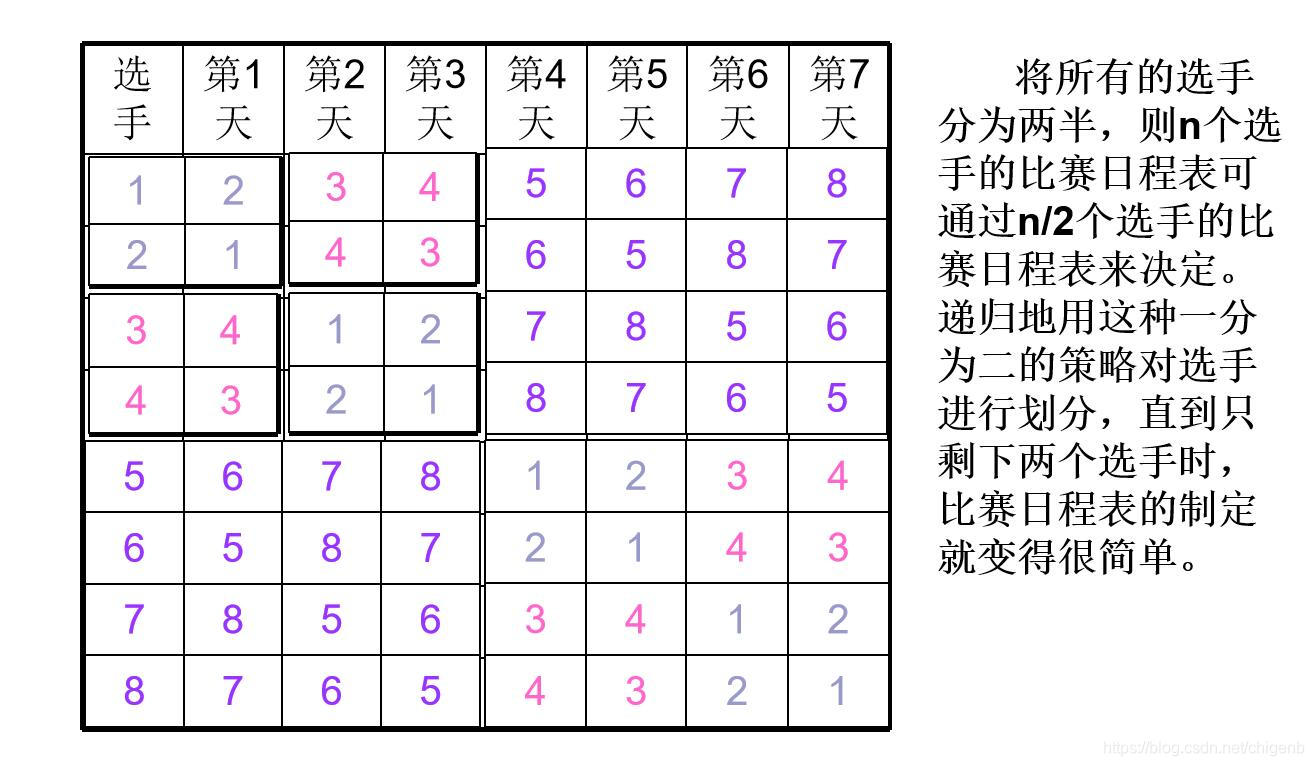
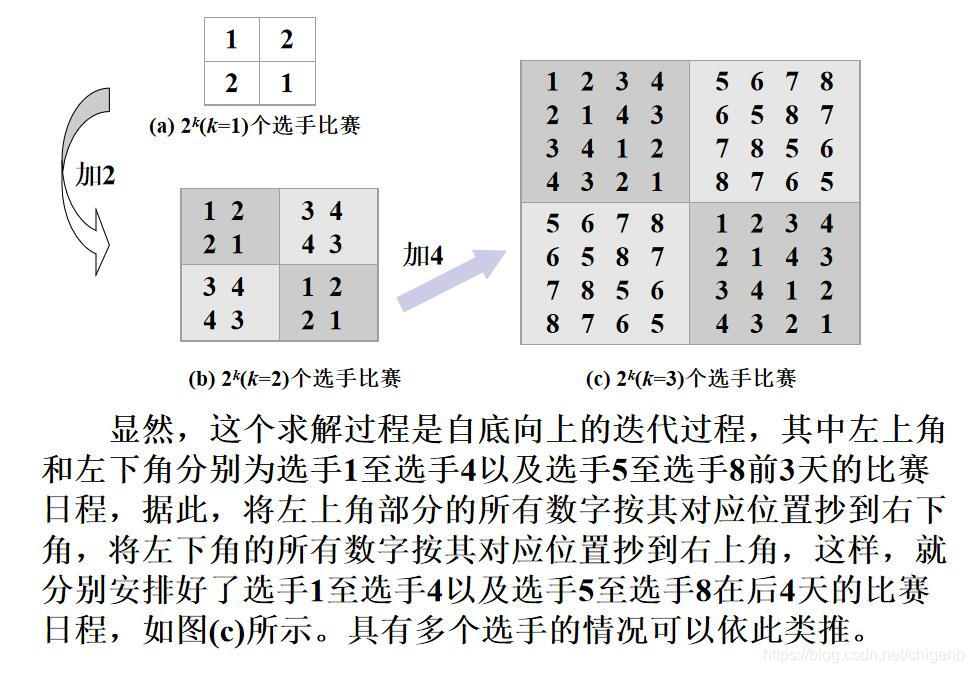
3、程序代码（非递归）

#include<iostream>
using namespace std;
#define N 8//运行结果正确，但是N不能太大，不然一个屏幕占不下
void table(int a[][N+1],int n)
{
	int i, j, t, temp;
	for (t = N; t >= 4; t = t / 2)//因为前4个格子已经填好，所以不必循环到t==2。迭代处理，依次处理2^2, …, 2^k个选手比赛日程
	{
		temp = n; n = n * 2;
		//填左下角元素
		for (i = temp + 1; i <= n; i++)
			for (j = 1; j <= temp; j++)
				a[i][j] = a[i - temp][j] + temp;		
		//填右上角元素
		for (i = 1; i <= temp; i++)
			for (j = temp + 1; j <= n; j++)
				a[i][j] = a[i + temp][(j + temp) % n];
		//填右下角元素
		for (i = temp + 1; i <= n; i++)
			for (j = temp + 1; j <= n; j++)
				a[i][j] = a[i - temp][j - temp];
	}
}
int main()
{
	cout << N << "名运动员比赛日程安排表" << endl << endl;
	int n, i, j, a[N + 1][N + 1] = { 0 };// n=2^k(k≥1)个选手参加比赛，二维数组a表示日程安排，数组下标从1开始（方便计算和书写）
	n = 2;      //先将左上角四个数写出来
	a[1][1] = 1; a[1][2] = 2;
	a[2][1] = 2; a[2][2] = 1;
	table(a,n);
	cout << "选手" << "\t";
	for (i = 1; i <= N-1; i++)
	{
		cout << "第" << i << "天" << "\t";
	}
	cout << endl;
	for (i = 1; i <= N; i++)
	{
		for (j = 1; j <= N; j++)
			cout << a[i][j] << "\t";
		cout << endl;
	}
	getchar();
	getchar();
	return 0;
}

4、程序代码（递归）

#include <iostream>
#include <algorithm>
using namespace std;
#define N 8
void table(int a[][N],int n, int temp)
{
	int i, j;
	if (n == 2) {
		a[1][1] = 1 ;
		a[1][2] = 2 ;
		a[2][1] = 2 ;
		a[2][2] = 1 ;
	}
	else {
		temp = temp / 2;  
		table(a, n / 2, temp);
		//填左下角元素
		for (i = temp + 1; i <= n; i++)
			for (j = 1; j <= temp; j++)
				a[i][j] = a[i - temp][j] + temp;		
		//填右上角元素
		for (i = 1; i <= temp; i++)
			for (j = temp + 1; j <= n; j++)
				a[i][j] = a[i + temp][(j + temp) % n];
		//填右下角元素
		for (i = temp + 1; i <= n; i++)
			for (j = temp + 1; j <= n; j++)
				a[i][j] = a[i - temp][j - temp];
	}
}
int main()
{
	int a[N][N] = { 0 }, temp = N, i, j;
	table(a, N, temp);
	cout << N << "名运动员比赛日程安排表" << endl << endl;
	cout << "选手" << "\t";
	for (i = 1; i <= N-1; i++)
	{
		cout << "第" << i << "天" << "\t";
	}
	cout << endl;
	for (i = 1; i <= N; i++)
	{
		for (j = 1; j <= N; j++)
			cout << a[i][j] << "\t";
		cout << endl;
	}
	getchar();
	getchar();
	return 0;
}

5、总结
其实递归与非递归差别并不大，循环赛问题的核心在于怎么由左上角的一个求出其他三个，或者由左上角及左下角的两个求出另两个（这是其他博主的做法），其实归根到底思路都是一样的，都是求坐标之间的关系。分析代码前先把讲解看懂，此题并不难。我也是学生，所以代码没有那么复杂，希望能给大家带来帮助。
6、Hebuters慎抄