12.4--九宫格数独

1.题目及概述

前几天没更新 所以说这几期的博客解析题目质量会高一些 我会尽量把自己的思路展现的更详细一些，弥补我前几天没发博客的过错，持续发的话自己时间不够，质量就可能会下降，所以接下来几期博客整点有质量的题目,在讲解过程中我会尽量详细的写出每个难以理解的地方所对应的基础知识点并体现出完整的思路历程。

2.分析题目，思考代码逻辑雏形

题目的输入是先输入一个整数，代表着接下来要检测几个九宫格数独，所以说在最开始可以用简易的循环来处理输入数据(例如while(n--),不用定义循环次数标志)，而在评判一个九宫格数独是否符合数独的要求之前，我们必须要先把这个九宫格数独储存起来，我觉得最容易想到的就是利用二维数组，把每一次循环输入的九宫格数独单独储存到一个九行九列的二维数组中，然后我对二维数组进行后期的逻辑处理。

有些人可能会想到一行一行的储存，我感觉这是非常的无厘头的，因为在后期我们对数独的处理必然包括每一行的检测，每一列的检测，每一个九宫格的检测，如果说按我们的思路来，把它储存在一个二维数组，我们后期处理的时候的逻辑底座扎实，不容易出错，也更符合编程的要求，所以在录入数据的时候，其实我们怎么做题，就已经被影响到了，我们在后期做题的时候，也尽量要把输入的数据以一种比较方便后期处理数据的方式输入，这样才能循序渐进，而不是吃一口不想着下一口，没有逻辑，没有效率。

这个时候，代码的雏形已经展现：

int main() {
    int n = 0;
    int arr[9][9] = {0};
    scanf("%d", &n);
    while (n--)
 {
        for (int i = 0; i < 9; i++) 
 {
            for (int j = 0; j < 9; j++) 
            {
                scanf("%d", &arr[i][j]);
            }
 }

其实在上文中已经提到了，我们如果说要检测一个数独是否符合，我们要对这个二维数组进行逻辑处理，什么逻辑处理呢？就是行的检测函数(LineJudge)，列的检测函数(RowJudge)，宫格的检测函数(SquareJudge),虽然说我们现在还没有写出函数的检测逻辑，但是我们可以先完成函数的声明以及后续代码的逻辑，如下：

#include <stdio.h>
#include <stdbool.h>

bool LineJudge(int (*p)[9]);
bool RowJudge(int (*p)[9]);
bool SquareJudge(int (*p)[9]);


int main() {
    int n = 0;
    int arr[9][9] = {0};
    scanf("%d", &n);
    while (n--) {
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                scanf("%d", &arr[i][j]);
            }
        }
        // 检测逻辑
        if (RowJudge(arr) && LineJudge(arr) && SquareJudge(arr)) {
            printf("Yes\n");
        } else {
            printf("No\n");
        }
    }
    return 0;
}

思考到这里，我们就可以开始着手于写出函数检测逻辑了

1.行检测逻辑与列检测逻辑

在说这个之前，可能会有人疑问为什么要传参arr，这里我解释一下，传参arr是比较方便的一种行为，你为你传arr，这个arr代表着首元素的地址，也就是第一个元素是第一个一维数组的数组名，arr的类型为数组指针，指向第一个元素，也就是第一个一维数组，解引用这个(arr + k)可以得到指向第k行(k从0开始)的数组指针，这个数组指针本身加减i ,又可以得到指向具体位置的一个整形指针，进可攻，退可守，这样的传参无疑是比较好的选择。

行检测逻辑无疑是最好想象的，因为行检测逻辑就是逐行检测，而每一行是一个一维数组，所以说这个循环并不难想，

首先：

这一定是一个双重循环，第一层循环代表从第0行到第8行（可以看出第一层循环循环9次），第二层循环代表从每一行开始遍历这个一维数组（由于这个一维数组有9个元素，可以看出第二层循环循环9次），检测这个一维数组是否满足数独的要求（出现1~9，不能重复，不能遗漏），这个逻辑有点难想，但是我之前做过一道题目，那一道题目给出了一个我难忘的逻辑：

如果检测是否满足数独逻辑，不如新定义一个一维数组，这个一维数组有10个元素，每个元素都是0，我不管索引为0的元素，仅仅关注索引1~9的元素（想想为什么？这里不给出解答），在第二层循环中，如果说解引用二元数组对应位置的数字为1，那么索引为1的新定义的一维数组+1,按照这个逻辑，我只需要在内层循环后再加一个循环去检测新定义的一维数组索引1~9是否等于1，如果有一个不是1，那么直接return false，全部都是1，那么这一行没有问题的，到最外层循环的外面的下面return true，但是之前你不要忘了，检测每一行的时候，这个新定义的数组都应该被重新初始化为每个元素为0，这样才能检测每一行检测的很舒服，给出行检测逻辑函数：

bool LineJudge(int (*p)[9]) {
    int a[10] = {0};
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            a[*(*(p + i) + j)]++;
        }
        for (int k = 1; k <= 9; k++) {
            if (a[k] != 1) return false;
        }
        // 重置计数器数组
        for (int k = 1; k <= 9; k++) {
            a[k] = 0;
        }
    }
    return true;
}

a[*(*(p + i) + j)]++：解释一下这个代码：

这里p代表arr,p+i代表指向第i行对应的数组的数组指针，*(p+i)，解引用这个数组指针得到一个数组，但准确来说是一个数组名，这个数组名又代表着首元素的指针,那么*(p + i)其实还是一个指针(其实因为p是一个二维数组名，解引用两次才能得到一个不是地址的东西，这里不再赘述)，(*(p + i) + j)表示的是从第一个元素开始向后移动 j 个 位置，指向第从左向右数第 j 个元素 (i,j均可为0)

说实在的，你别不信，列检测逻辑，仅仅需要调换这个代码中两个字符的位置，先给出代码后，在给出解析：

bool RowJudge(int (*p)[9]) {
    int a[10] = {0};
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            a[*(*(p + j) + i)]++;
        }
        for (int k = 1; k <= 9; k++) {
            if (a[k] != 1) return false;
        }
        // 重置计数器数组
        for (int k = 1; k <= 9; k++) {
            a[k] = 0;
        }
    }
    return true;
}

可以看到仅仅是：

a[*(*(p + i) + j)]++ --->a[*(*(p + j) + i)]++;

为什么呢？

第一次行检测逻辑我需要遍历的是(拿第一行举例):

00 01 02 03 04 05 06 07

第一次列检测逻辑我需要遍历的是(拿第一列举例):

00 10 20 30 40 50 60 70

举个这个例子，你就可以明白为什么是这么交换就可以实现列检测逻辑，在平时写代码的时候，也要多有这种“局部特征代替整体规律”的思路，举一个（局部特征）例子，你就可以料到这行（整体规律）代码该怎么写了。

2.宫格检测逻辑

宫格检测逻辑是比较复杂的，但是也不是特别不好切入思维，不妨我们这么想，我们先找到一个可以被我们施加连贯逻辑的地方实施我们的宫格检测逻辑，就比如下图，我们可以在每一个九宫格的左上角来作为起始逻辑，肯定会有双层循环，第一个循环循环9次，表示检测9个九宫格，每个九宫格会检测9个数字，这就是内部逻辑，

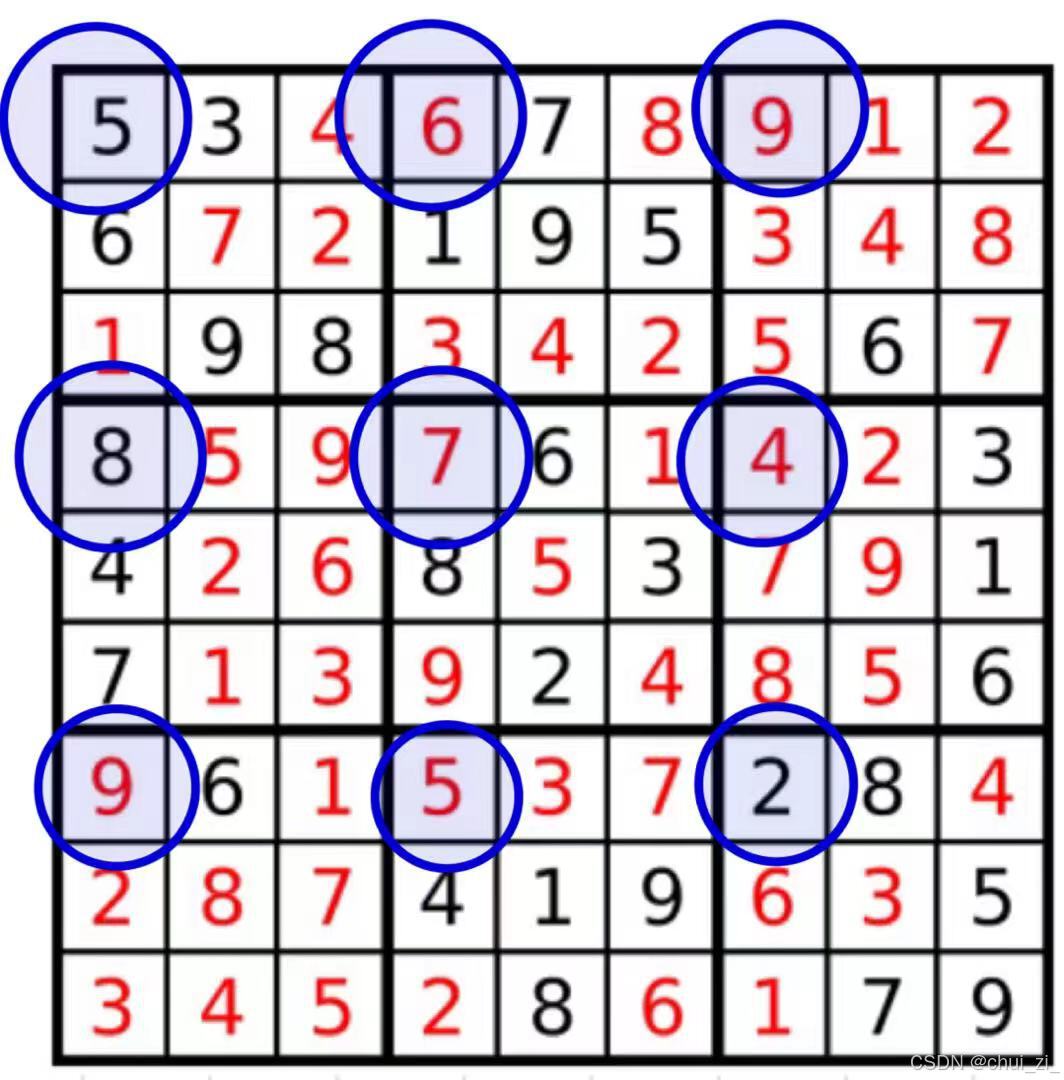
但是我们去设计一个外层循环就会发现一个非常棘手的问题：

在这里i = 0;i < 9;i++所对应的逻辑如下：

我们要逐层使i表示

00 03 06

30 33 36

60 63 66

问题来了：一个从0~8的数字,我怎么实现一个逻辑（先按行来看），使得在i = 0 1 2的时候表示0,

i = 3 4 5的时候表示3，i = 6 7 8的时候表示6？这听上去是不是很像分段函数，我们再用i去表示一个关于i的函数的时候，我们可以表示一次函数(k * i + b)，可以表示二次函数及以上，可以借助math.h头文件表示指数函数和对数函数，三角函数，反三角函数，但是我们却没有办法直接的用一个完备的关于i的表达式去表达i的一个分段函数，我们该怎么办？我们怎么样才能书写出这样的逻辑？------ 新设立一个返回值为int的求值函数就可以了，具体实现如下，用于表示，求对应的行数和列数：

int Change1(int i) {
    if (i == 0 || i == 1 || i == 2) return 0;
    else if (i == 3 || i == 4 || i == 5) return 3;
    else return 6;
}

int Change2(int i)
 {
    if (i == 0 || i == 3 || i == 6) return 0;
    else if (i == 1 || i == 4 || i == 7) return 3;
    else return 6;
}

那么写到这里，我们怎么实现九宫格的检测逻辑呢？

即使我们找到了每一个九宫格的“起始元素”该如何表示，但是我们也要从这个起始元素开始遍历整个九宫格，这仍然意味着我们需要设立嵌套循环去完善检测逻辑

a[*(*(p + startRow + i) + startCol + j)]++;

关键是要理解这个代码，(p + startRow + i)表示指向第startRow + i个一维数组，对其解引用代表着这个数组名，也代表着这个数组的首元素的地址，后续加上startCol和j也是为了找到这个一维数组从左向右数的第startCol + j个元素 这里的startCol和startRow可以被理解为初始化这个循环的检测逻辑，也就是提前先把哪个九宫格的元素给你指引到位，在根据i和j的嵌套循环在九宫格内便利，计数一维数组的逻辑与上文相同，这里不再赘述

bool SquareJudge(int (*p)[9]) {
    int a[10] = {0};
    for (int block = 0; block < 9; block++) 
	{
        int startRow = Change1(block);
        int startCol = Change2(block);
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                a[*(*(p + startRow + i) + startCol + j)]++;
            }
        }
        for (int k = 1; k <= 9; k++) {
            if (a[k] != 1) return false;
        }
        // 重置计数器数组
        for (int k = 1; k <= 9; k++) {
            a[k] = 0;
        }
    }
    return true;
}

3.完整代码实现

#include <stdio.h>
#include <stdbool.h>

bool LineJudge(int (*p)[9]);
bool RowJudge(int (*p)[9]);
bool SquareJudge(int (*p)[9]);
int Change1(int i);
int Change2(int i);

int main() {
    int n = 0;
    int arr[9][9] = {0};
    scanf("%d", &n);
    while (n--) {
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                scanf("%d", &arr[i][j]);
            }
        }
        // 检测逻辑
        if (RowJudge(arr) && LineJudge(arr) && SquareJudge(arr)) {
            printf("Yes\n");
        } else {
            printf("No\n");
        }
    }
    return 0;
}

bool LineJudge(int (*p)[9]) {
    int a[10] = {0};
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            a[*(*(p + i) + j)]++;
        }
        for (int k = 1; k <= 9; k++) {
            if (a[k] != 1) return false;
        }
        // 重置计数器数组
        for (int k = 1; k <= 9; k++) {
            a[k] = 0;
        }
    }
    return true;
}

bool RowJudge(int (*p)[9]) {
    int a[10] = {0};
    for (int i = 0; i < 9; i++) {
        for (int j = 0; j < 9; j++) {
            a[*(*(p + j) + i)]++;
        }
        for (int k = 1; k <= 9; k++) {
            if (a[k] != 1) return false;
        }
        // 重置计数器数组
        for (int k = 1; k <= 9; k++) {
            a[k] = 0;
        }
    }
    return true;
}

bool SquareJudge(int (*p)[9]) {
    int a[10] = {0};
    for (int block = 0; block < 9; block++) 
	{
        int startRow = Change1(block);
        int startCol = Change2(block);
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                a[*(*(p + startRow + i) + startCol + j)]++;
            }
        }
        for (int k = 1; k <= 9; k++) {
            if (a[k] != 1) return false;
        }
        // 重置计数器数组
        for (int k = 1; k <= 9; k++) {
            a[k] = 0;
        }
    }
    return true;
}

int Change1(int i) {
    if (i == 0 || i == 1 || i == 2) return 0;
    else if (i == 3 || i == 4 || i == 5) return 3;
    else return 6;
}

int Change2(int i)
 {
    if (i == 0 || i == 3 || i == 6) return 0;
    else if (i == 1 || i == 4 || i == 7) return 3;
    else return 6;
}

4.下期预告:夺旗