1,对于有模的计算:
模的概念:(个人理解)
模就是一个数值范围的大小规模。
举个例子:比如有一个一维坐标,值的范围是0到19,取整。那么它的模就是20,因为它可以有20个元素。
然后把这个一维坐标首位相接,但是不重合,那么就形成了一个圈,0-------19-0---------19-0,这样的循环过程。
也就是说如果在这个圈里面取值,就是在这个圈循环的找值,就类似于取余了。
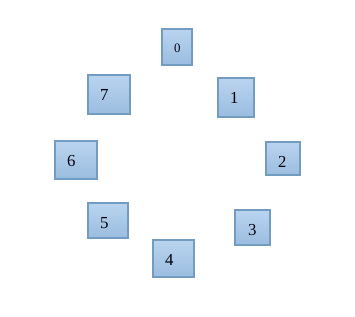
就这样数值在这里面的计算的值就是这里面的数。
模中的计算:
如何计算一个值在模中的“位置”呢?
使用求余的手段。
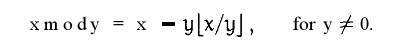
这样就可找到值在这个圈中的位置了,这个圈中的值是从0到7的,它的模是8。(以下的解释都使用这个来做例子,为了方便理解)
在一个有数值范围的计算中,计算的过程就像在一个圆圈中“旅行”。
2,没有符号的计算:
到这里,大家对模的理解应该有认识了,但是对于为什么使用补码好像没有多大的关系?(不急)
在没有符号的计算过程中,貌似值就是整数值,所以表示的话使用普通的二进制的值就够了。
计算的过程中不会涉及到真值在计算过程中的表示问题。
所以在二进制中的计算是基本没有问题的。
上例子:
(对于模8来说的)
5 + 4 = ? (不要以为是9哦)
5+4 = 9 (我了去,真的是9)
9 mod 8 = 9 - 8( 9/8 ) (小括号小表示以下取下界咯)
= 9 - 8 (由于取整,所以小数就去掉了)
=1 (咿,是 1 哟)
(如果觉得不理解,可以数那个圈拉?嘻嘻)
也就是说在这个圈里面的计算基本没有什么问题啦。。。。。。。。。。。3,有符号之后的计算变化:
有符号之后的表示:
在计算机里面是有符号的,那么表示时候就没有那么好直观咯。
在计算机中的符号的表示是使用0和1来表示的, 就是 0 为正 1 为负。
那么上面的图就变成了:

这鬼样。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。嘻嘻
有符号的阻碍:
那么计算呢?就有点小麻烦了。
这样虽然模还是8,但是你会发现计算的过程的模是4了,因为分割成两类之后,它的模表示范围会缩小一半。
所以现在的模是4(这里的模是表示值的模,而不是真正的模哦)。
好吧,先把它变成二进制吧:
-4 ?
-3 --------> 111
-2 --------> 110
-1 --------> 101
-0 ?
0 --------> 000
1 --------> 001
2 --------> 010
3 --------> 011咿,怎么有两个那么奇怪的值?等一下再解释。
先来看看正常的。 -1 -2 -3 1 2 3
它们除了符号之外值是一样的。。。。。这样就可以表示成 正负号的值了,但是计算的时候就有问题了。
上例子:
-3 + 3 = ? (是 0 么 ? )
表面上就是 0 啦,但是转换成二进制之后呢?
-3 = 111
3 = 011
111
+ 011
---------------------------
(1)010 (括号的不要,溢出了嘛) 2又来一个“咿” ,怎么不是0呢? 是2呢? 为什么呢?
有符号计算,补码的出现:
如果你放到没有符号的计算是完全正确的,但是放在这里就有问题咯。
这是为什么?
因为转换成二进制之后就是二进制的计算,在我们的二进制里面根本就不会有正负之分,而只有数值大小的区别,所以呢?实际上是在模8中计算的过程,
而我们本身的思维是把它当作是有符号的计算。(那就。。。。。。。。。。是思维问题,不是数学本身的问题)
在模值固定的情况下,改变数值的表现形式,数值在模值中的位置没有改变,只是表现的形式改变了。在这个模值范围里是没有问题的。
那如何做,才能实现正负的计算呢?
这个时候我们的计算里面是含有符号的概念的,所以计算的过程符号的概念使得计算被模糊了。(就是符号到底是参加计算还是不参加计算)
补码转换:
好,那就先说说一下实际的例子,来解决补码转换:
到时钟的问题上:
回拨2小时 = 前拨10小时
回拨4小时 = 前拨8小时
回拨5小时= 前拨7小时
假设时钟只有8个数字,那么就变成了。
回拨2小时 = 前拨6小时
回拨4小时 = 前拨4小时
回拨5小时= 前拨3小时
也就变成了我的 -2 可以使用 +6 来表示。。。。。。。
那么 -3 可以使用 +5来表示么?
不是可以用来表示,而是可以实现同样的运算效果,那就看成是等价吧。
所以有补码的出现咯,看!补码来了。。。。。。。。。。。。。。。。。。。。。。。。。。。
补码 = 反码 + 1 (原码 + 反码 + 1 = 模,所以补码和原码是互补的,所以就是这样子咯)
也就是说在模值固定的情况下,可以作出数值伸缩,就是大小表示范围,但是元素的个数不会改变。
由于数值有符号,所以数值的表现是原来的一半,为了使得计算的过程中忽略符号的存在,把减法变成加法。
这时,我们需要扩大数值表现,使得计算的过程是二进制正数的普通运算。
把有符号的数值,转换成无符号区别的数值。
以时钟的思想来说,正数和负数的加法是两个正数的减法,我们再把减法变成了加法,这样补码就有作用了。但是我们怎么知道它是对的呢?
对于有模值来说,我们就可以使用时钟的思想来实现同样的效果。
举个例子:
3+(-3) = 3 - 3 = 3 + 5
于是,我们就可以把符号的模糊性给明确了,转换之后就没有符号的概念了,我们就可以直接使用二进制的普通计算啦!
那么减法就变成了加法:
101
011
---------------
000
结果是 000 转换成真值就是000咯。正数。(对了。。。。。)
这样我们就解决了有符号计算的问题。
计算出来的值是没有符号的区别的,因为数值真值是有符号的区别,所以表示的值的上限也减少了一半,所以如果最高位出现1的话,真值是无法表示的,所以使用同余转换成负值来表示。
由于我们在计算的时候是扩充了数值,所以在转换的时候为了数值真值的表现,我们需要再次缩小数值,通过负转换来实现。
结果的转换:
假如一个计算的结果是 111
对于没有符号来说。
二进制的值是 7
7 = 0 + 7
7 = 0 - 1
这是因为在模值的这个圈中,是一样的位置。
也就是说你的数值表示不一样,但是位置是一样的,所以在计算的时候绕着这个圈“旅行”是说的通的。
等效的表示后,缩小了数值表示,就会出现在可显示真值范围内了。
7 的等价转换是 -1.
就是说:
模值是 8
有正负之分,那么正数可以表示的值的上限是 3 ,如果结果是一个 5 呢?
可以这么解释:
看成是与 0 的偏移量。
3 = 0 + 3
5 = 0 + 5 = 0 - 3 (效果是一样的,所以它们最终到达的点是一样的,那么值就是一样的,对于有模来说)
所以值我们就可以使用
-3 来表示 5。(-3 的值使用二进制的5来等效表示,正好 101,再转换的时候,也就是求补 变成 111 ,这时候就是有符号的区别了,不再是7了。)
上例子:
010
101
-----------------------------
111
看,大于 3的值,如果转换成真值就是 7 ,不对。
由于计算的时候,不区分正负,所以结果是不区分正负的,因为之前我们使用最高位去实现符号位,这个位也说明它是否需要转换的标志。
由于计算效果是一样的,所以跟我们正常的思维来说,同余转换过后的结果是符合我们的。
111 是计算时候使用值,带有符号的表示的时候是不适用的,需要逆转换。
逆转换一下 111 ------> 101 这时候就是真值了,有符号位哦, 所以 是 -1啦。
那么结果就是 -1 ,因为正值无法表示 7 所以使用负值来表示。
而现在的二进制 7 是用来表示 -1回来。
这样就可以是区分正负咯。
这样也就实现了,计算过程中没有正负之分,而结果可以有正负之分的转换。
小结一下:
在二进制中我们就可以这么想:
以 0 为 标准 ,其余的值是偏移量,分正偏移和负偏移。想是这么想的,但是偏移量之间的计算呢?为了不考虑符号的问题,等价的转换成相同符号来计算。
而计算后,得到的值在偏移量中超出,那么我们就可以使用一个圈的形式去防止数值超出表示范围。
所以我们就可以使用等等效的负偏移的方法来实现超出的值。
正好这个超出的值和负偏移之间的转换是一个同余的转换形式,所以就可以使用补码的形式去转换,就形成了我们所说的 结果是负数的值进行补码的转换成真值的说法。
而对于可以显示的正数来说,它根本就是没有溢出的可能,所以不需要补码的转换,那就是 正数的补码还是原来的数。
涉及到了真值和补码之间的转换,如何转换呢?
补码 = 反码 + 1 (原码 + 反码 + 1 = 模,所以补码和原码是互补的,所以就是这样子咯)
这样,我们就可以实现了,正负的计算,最终结果还是正确的。
对于正数来说补码的作用就相当于没有,但是对于负数来说,就会出现符号位的区别,所以补码的参与使得计算过程被简化。
其实我觉得就是以补码作为一个计算的盒子,结果又被转换成真值。
主要补码可以实现把有符号的数转换位无符号的数,也可以再转换位有符号的数,无符号的计算是没有问题(因为模值等效那个过程引起的),所以补码很有用,结果可以使用补码的形式去转换会真值(也是模值等效转换引起的)。
那补码的作用是?
为了实现在二进制中有符号数的计算。
过程也就变成一般的过程:
真值变成补码,补码计算,补码转换的过程。
在有符号的计算中使用了补码的方法,简化的计算的过程,使得在计算机中的计算很明确。
5,在计算机里面的二进制计算:
在计算机里面就是把数值变成补码来计算的,然后再把补码转换成真值。





















 791
791

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








