How to print a tree-ADT ? 打印树形结构的算法

How to print a tree-ADT

写和树相关的代码的时候老是不方便debug，因为树形结构虽然能够代码构造出来

但是如果能够有个很好的方法可视化就更好了。

前些天看到一个MIT的代码片段，感激～....

一开始你可能会想到一种比较简单的迭代实现，就像之前我做的

1. void putout(int S, int *n)  

实现在这里

http://blog.csdn.net/cinmyheart/article/details/43086233

这个函数会打印一个三角形

而我看到MIT老师准备的教学用的Python代码时就眼前一亮的感觉，有了一种更“精准的“打印三角形的策略——基于递归。

    def _str(self):
        """Internal method for ASCII art."""
        label = str(self.key)
        if self.left is None:
            left_lines, left_pos, left_width = [], 0, 0
        else:
            left_lines, left_pos, left_width = self.left._str()
        if self.right is None:
            right_lines, right_pos, right_width = [], 0, 0
        else:
            right_lines, right_pos, right_width = self.right._str()
        middle = max(right_pos + left_width - left_pos + 1, len(label), 2)
        pos = left_pos + middle // 2
        width = left_pos + middle + right_width - right_pos
        while len(left_lines) < len(right_lines):
            left_lines.append(' ' * left_width)
        while len(right_lines) < len(left_lines):
            right_lines.append(' ' * right_width)
        if (middle - len(label)) % 2 == 1 and self.parent is not None and \
           self is self.parent.left and len(label) < middle:
            label += '.'
        label = label.center(middle, '.')
        if label[0] == '.': label = ' ' + label[1:]
        if label[-1] == '.': label = label[:-1] + ' '
        lines = [' ' * left_pos + label + ' ' * (right_width - right_pos),
                 ' ' * left_pos + '/' + ' ' * (middle-2) +
                 '\\' + ' ' * (right_width - right_pos)] + \
          [left_line + ' ' * (width - left_width - right_width) + right_line
           for left_line, right_line in zip(left_lines, right_lines)]
        return lines, pos, width
    def __str__(self):
        return '\n'.join(self._str()[0])

代码没给注释，折腾我好些时候。。。递归。。。

（过段时间我再注释，先把代码贴出来）

下面是个的改动版本，还有点需要完善的地方，不过还能凑合用：

    def __str__(self):
        def recurse(node) :
            if node is None:
                return [], 0, 0
            else :
                left_lines, left_pos, left_width = recurse(node.left)
                right_lines, right_pos, right_width = recurse(node.right)

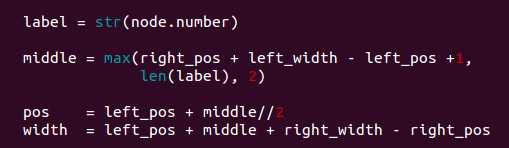
                label = str(node.number)
                middle = max(right_pos + left_width - left_pos +1,
                        len(label), 2)

                pos    = left_pos + middle//2
                width  = left_pos + middle + right_width - right_pos

                while len(left_lines) < len(right_lines) :
                    left_lines.append(' ' * left_width)
                while len(right_lines) < len(left_lines) :
                    right_lines.append(' ' * right_width)

                line   = [' ' * left_pos + label + 
                          ' ' * (right_width-right_pos + 1),
                          ' ' * left_pos + '/' + 
                          ' ' * (middle-2) + '\\' +
                          ' ' * (right_width - right_pos)
                                    ] + \
                         [
                            left_line + 
                            ' ' * (width - left_width - right_width) +
                            right_line 
                            for left_line, right_line 
                            in zip(left_lines, right_lines)
                                    ]

                if node is self.root :
                    return line
                else :
                    return line, pos, width

        if self.root is None :
           return '<Empty tree>'

        output = recurse(self.root)
        for i in range(1, len(output)-2) :
          output[0] += '\n' + output[i]

        return output[0]+'\n'

demo:

大体的树形结构和层次是清楚的

两份代码都会做分析。

2015.02.03 update

1.我改动的代码实现原理分析：

首先，我们要明白我们讨论的对象用哪些名词术语描述（这个很重要，不然看裸代码很蛋疼）

这里有点递归定义的赶脚。。。，会发现，pos定义的时候涉及了middle， middle在pos之前定义，而middle的定义又涉及rihgt_pos, left_pos，而这两个变量由pos定义。。。

lines ：表示等待打印的树形结构，就是个字符串，按照顺序打印可以打印出树形结构。

            对于左右不同的子树，用 left_lines 和right_lines表示

pos : 表示当前树结构的根节点的位置（偏移量）。

middle：表示字符‘/‘ ’\‘ 之间的距离（这里包括这两个字符，即距离大于等于2）。

width： 表示右子树根节点与本行开头的距离。

left_pos就是左子树的根位置，right_pos就是右子树的根位置，两树合并前相互独立，即处于不同的line变量

中——left_lines, right_lines。

2015.04.02　更新．之前代码的缩进有点不对，做出的修正