详细讲解RC积分电路

从干硬件的第一天起，接触最多的就是RC串联，大部分时候我们都将其作为低通滤波器滤除干扰。也有时候，用到其积分器的功能，但不知其所以然。今天就从头到尾，就这一个最简单最基础的东西，讲解其背后的原理。

首先根据基尔霍夫电压定律和电容的电流-电压关系：Vin=IR+Vc，而电容的电流I=C·（dv/dt），因此

 

这个式子很熟悉，再一细看，就是一阶微分方程。下面先回顾一下一阶微分方程。

形如

其通解为

因此将上式整理为标准的一阶微分方程的形式：

则很容易得出

假设t=0时刻，电容两端电压就有V（0），则代入上式可解的C=V（0）

则最终解为：

（注意这的τ还不是时间常数τ，只是一个变量，因为积分里面已经有t了）

对于输入方波信号，在每个周期的高电平和低电平都是恒定的电压，在电容充放电到达稳态的时候，表现为在高电平充电，低电平放电，因此上式可继续化简。

令输入电压Vin（t）=Vfinal。

先计算

代入上式得

继续展开化简

最终得

其中τ=RC，为时间常数。

下面具体举例计算，输入方波经过RC积分电路，输出波形是什么样的。

输入一个1.638/3.276V 500Hz的方波，经过20K+0.47uF，求输出波形。

首先计算时间常数τ=RC=20·0.47=9.4ms。方波周期T=1/500=2ms。

因为电容充放电后一定会进入到一个稳态，此时在方波的高电平表现为充电，低电平表现为放电。设此时稳态的初始值为V0，则电容电压在下一个方波周期到来时，在方波的高电平充电为V1，在方波的低电平放电为V2，因为稳态时电容电压在这一周期结束时回到初始值，则可得到V2=V0。

下面来求解这个稳态V0。

（1）充电阶段（高电平3.276V）

因为方波的占空比就是50%，因此充电和放电时间都为T/2=1ms。

电容从V0开始充电1s后到V1

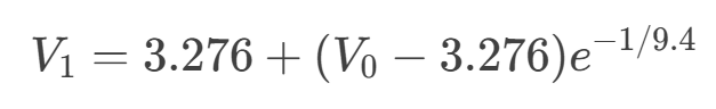······①

（2）放电阶段（低电平1.638V）

电容从V1放电1s后到V2

······②

注意到刚刚说的，V2=V0，联立①和②，代入V2=V0，可得

化简后可得，V0=2.406V，V1=2.494V。

也就是说稳态波动范围为：V0到V1之间。

用multism仿真波形如下：

为什么电容一定能到达充放电平衡的稳态呢？

从图里可以看出，在刚上电时，电容由于两端电压为0V，输入的方波1.638/3.276V，对电容来说，不管是高电平3.276V还是低电平1.638V，对于初始状态为0V的电容来说都是高电平，所以一直表现为充电状态。知道电容两端电压超过1.638V后，这是方波的高电平状态仍然表现为充电，但低电平1.638V相对于电容两端电压来说相当于是放电，只不过这时充的电比放的电多，电容两端电压还在升高。直到升高到一个稳态的点，这时在方波的每个周期内，电容充的电和电容放的电一样多，达到一个稳态平衡。

再回过头来看，就是一个极其简单的RC积分电路，若是从数学的角度来分析，计算量实在是太庞大。在实际工程应用中完全没有必要这样来计算。

首先要明白为什么要用RC积分电路？对于一个方波信号来说（广义上可以说是脉冲信号，只不过方波的占空比正好是50%）由图上可见，经过RC之后的波形是一个锯齿波，但锯齿波的振幅如果很小，就近似为一条直线，我们可以近似看作是恒定的直流电压。也就是说，通过积分电路可以将频率信号转化为电压信号，供单片机采集。

仔细研究不难发现，频率不变的情况下脉冲信号的占空比越高，也就是说电容充电的时间比放电的时间多，电容的电压也就充的越多，因此最后得到的锯齿波的平均值更高；

 

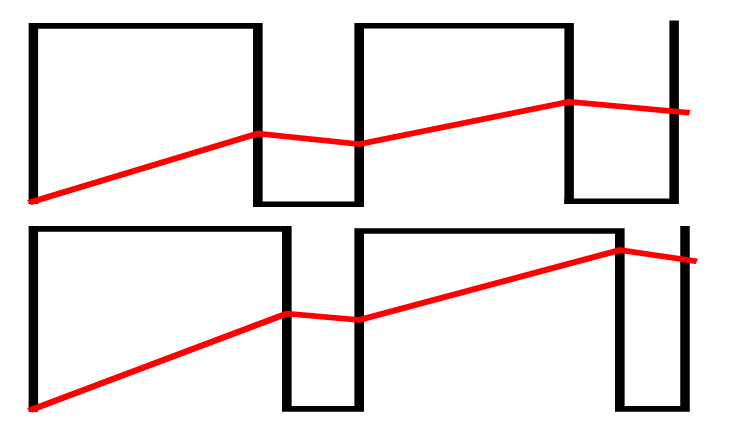
而占空比不变的情况下脉冲信号的频率越高，也就是电容充放电的时间很短，因此锯齿波的上下振幅越小，越近似于一条直线。

因此要想使输入的脉冲信号经过RC积分电路近似为一条直线供单片机采集，可以根据输入信号的频率，选取相应的R和C，保证时间常数RC远大于输入信号的周期。然后再用multism仿真看下波形，微调参数。（这里也可以从另一个角度理解，我们知道RC的截止频率f=1/2πRC，截止频率越小，信号的幅值衰减也更严重。上述举的例子输入信号500Hz，20K+0.47uF，则截止频率f=16.9Hz相对于输入500Hz就很小，幅值受到了非常大的衰减）