一、同态滤波
对于一幅由物理过程产生的图像f(x,y),可以表示为照射分量i(x,y)和反射分量r(x,y)的乘积。0<i(x,y)<∞,0<r(x,y)<1。i(x,y)描述景物的照明,变化缓慢,处于低频成分。r(x,y)描述景物的细节,变化较快,处于高频成分。
因为该性质是乘性的,所以不能直接使用傅里叶变换对i(x,y)和r(x,y)进行控制,因此可以先对f(x,y)取对数,分离i(x,y)和r(x,y)。令z(x,y) = ln f(x,y) = ln i(x,y) + ln r(x,y)。在这个过程中,由于f(x,y)的取值范围为[0, L-1],为了避免出现ln(0)的情况,故采用ln ( f(x,y) + 1 ) 来计算。
然后取傅里叶变换,得到 Z(u,v) = Fi(u,v) + Fr(u,v)。
然后使用一个滤波器,对Z(u,v)进行滤波,有 S(u,v) = H(u,v) Z(u,v) = H(u,v)Fi(u,v) + H(u,v)Fr(u,v)。
滤波后,进行反傅里叶变换,有 s(x, y) = IDFT( S(u,v) )。
最后,反对数(取指数),得到最后处理后的图像。g(x,y) = exp^(s(x,y)) = i0(x,y)+r0(x,y)。由于我们之前使用ln ( f(x,y)+1),因此此处使用exp^(s(x,y)) - 1。 i0(x,y)和r0(x,y)分别是处理后图像的照射分量和入射分量。
二、滤波器H(u,v)
由于我们会得到动态范围很大,但我们感兴趣的部分很暗,无法辨认细节的图像。这可以认为或者实际上就是由于光照不均所造成的。为了减少光照的影响,增强图像的高频部分的细节,我们可以使用同态滤波来增强对比度,增强细节。
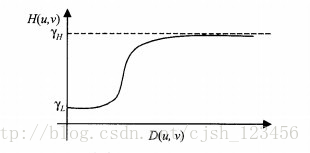
在此情况下,我们可以通过衰减低频成分,增强高频成分来达到我们的目的。通常可以采用如下高斯高通滤波器的变形滤波来对图像进行处理。
其中,选择rh > 1, rl < 1可以达到衰减低频,增强高频的目的,常数c控制函数坡度的锐利度。D(u,v)和D0与我们之前说低通滤波的时候意义一样。分别表示和频率中心的距离和截止频率。D0越大,对细节的增强越明显,最后归一化之后显示的图像越亮。对于不同的图像,D0的取值差别很大。对于特定的D0,有的图像显示之后是黑乎乎的一片,而有的图像却是整体白亮。
三、代码实现
在使用matlab代码使用如上所说的滤波器H(u,v)进行同态滤波的时候,基本过程和我们之前介绍进行低通滤波器的时候,进行频率域滤波的过程基本一致。理想低通滤波器、Butterworth滤波器和高斯滤波器(matlab)
只不过,在填充图像之前,先对图像进行对数化。在最后提取左上角的部分之后,对图像进行反对数化(取指数),然后再归一化,得到最终的图像。
1. 同态滤波函数代码如下:
该函数为HomoFilter,输入为需要进行同态滤波的灰度图像(灰度级L = 256),同态滤波器的参数rh,rl,c和D0。输出为滤波后的图像(已经归一化到[0, L-1])。
function [image_out] = HomoFilter(image_in, rh, rl, c, D0)
% 同态滤波器
% 输入为需要进行滤波的灰度图像,同态滤波器的参数rh, rl,c, D0
% 输出为进行滤波之后的灰度图像
[m, n] = size(image_in);
P = 2*m;
Q = 2*n;
% 取对数
image1 = log(double(image_in) + 1);
fp = zeros(P, Q);
%对图像填充0,并且乘以(-1)^(x+y) 以移到变换中心
for i = 1 : m
for j = 1 : n
fp(i, j) = double(image1(i, j)) * (-1)^(i+j);
end
end
% 对填充后的图像进行傅里叶变换
F1 = fft2(fp);
% 生成同态滤波函数,中心在(m+1,n+1)
Homo = zeros(P, Q);
a = D0^2; % 计算一些不变的中间参数
r = rh-rl;
for u = 1 : P
for v = 1 : Q
temp = (u-(m+1.0))^2 + (v-(n+1.0))^2;
Homo(u, v) = r * (1-exp((-c)*(temp/a))) + rl;
end
end
%进行滤波
G = F1 .* Homo;
% 反傅里叶变换
gp = ifft2(G);
% 处理得到的图像
image_out = zeros(m, n, 'uint8');
gp = real(gp);
g = zeros(m, n);
for i = 1 : m
for j = 1 : n
g(i, j) = gp(i, j) * (-1)^(i+j);
end
end
% 指数处理
ge = exp(g)-1;
% 归一化到[0, L-1]
mmax = max(ge(:));
mmin = min(ge(:));
range = mmax-mmin;
for i = 1 : m
for j = 1 : n
image_out(i,j) = uint8(255 * (ge(i, j)-mmin) / range);
end
end
end
2. 测试代码如下:
clear all;
close all;
clc;
image1 = imread('10.bmp');
[m, n] = size(image1);
image2 = HomoFilter(image1, 2, 0.25, 1, 80);
% 显示图像
subplot(1,2,1), imshow(image1), title('原图像');
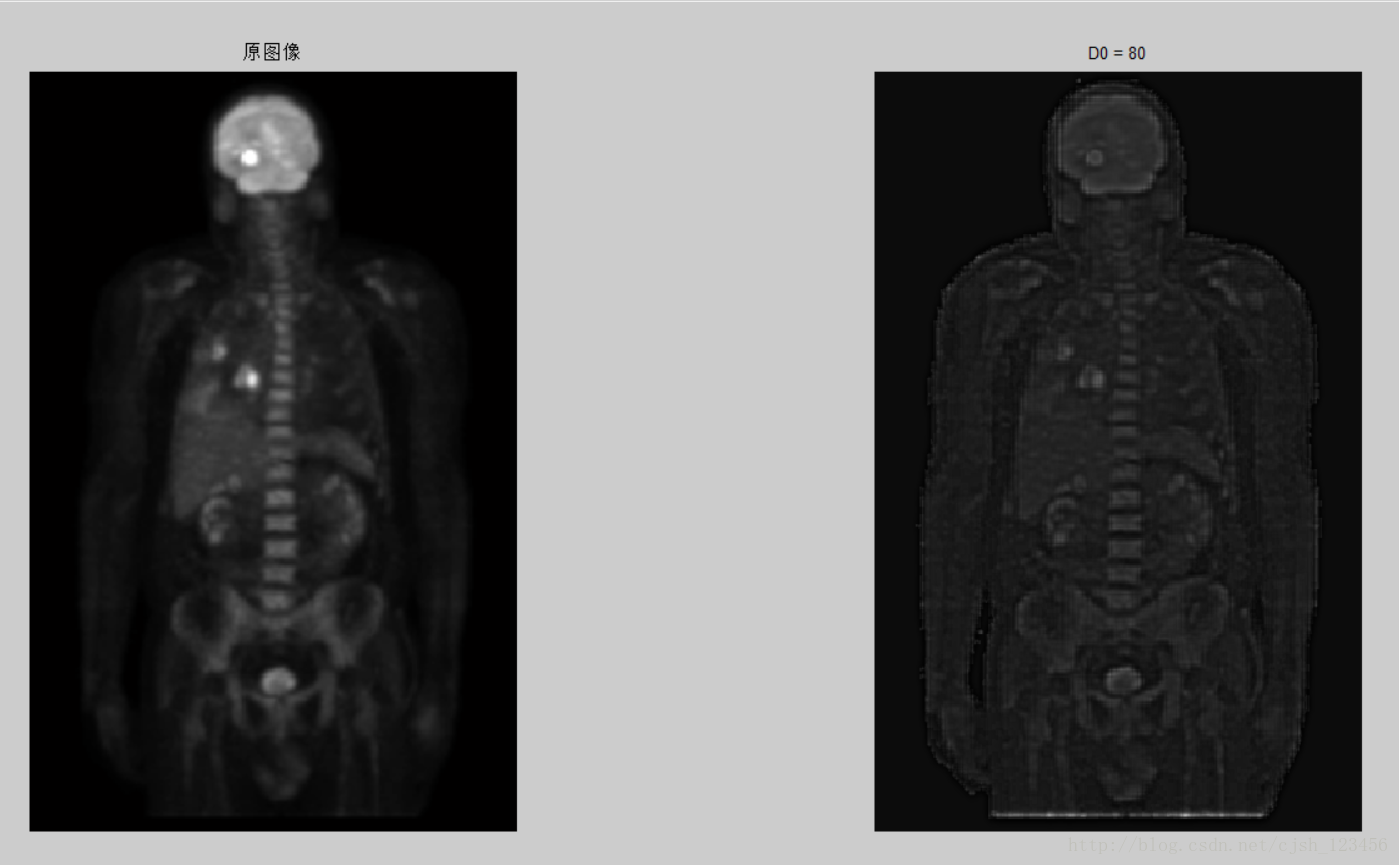
subplot(1,2,2), imshow(image2), title('D0 = 80');3. 结果如下:
可以看到,经过同态滤波之后的图像,图像可以看到更多的细节,降低了照射分量的影响。
下面是对另一幅图像的同态滤波结果,可以看到,对于D0与上面一样,都为80的情况下,图片一片黑乎乎。当D0等于500的时候,可以看到很多的细节。说明了对于不同的图像,D0的差别可能很大。









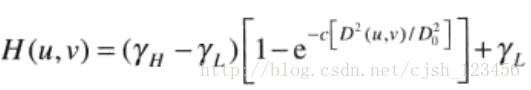

















 1376
1376

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








