函数的极限

一、自变量趋近于有限值时函数的极限

1.函数极限定义之描述性定义：

如果在 𝑥→𝑥₀ 的过程中，对应函数值 𝑓(𝑥) 无限接近于确定的常数 𝐴 ，那么就说 𝐴 是 𝑓(𝑥) 当 𝑥→𝑥₀ 时的极限。记作

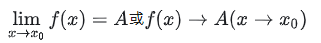
函数 𝑓(𝑥) 无限接近于常数 𝐴，就是 |𝑓(𝑥)−𝐴| 可以任意小，小到什么程度呢？就是可以小到你事先任意给定的任意小正数 𝜀 ，即 |𝑓(𝑥)−𝐴|<𝜀 。所以我们说𝑓(𝑥) 无限接近于常数 𝐴，是用 |𝑓(𝑥)−𝐴|<𝜀来刻画的。

 𝑓(𝑥) 无限接近于常数 𝐴，是在哪个过程中实现的呢？

是在 𝑥→𝑥0 的过程中实现的。所以只是对 𝑥0 附近的(或者说无限接近于 𝑥0 的)那些点，函数值满足|𝑓(𝑥)−𝐴|<𝜀( 𝜀 为任意给定的正数，可以任意小)。那么对 𝑥0 附近的 𝑥 ，我们怎么刻画呢？我们可以这样刻画： 0<|𝑥−𝑥0|<𝛿 ， 𝛿 为某一个正数，用几何意义来说就是，在 𝑥0 的某一个去心邻域内(心邻域即在a的 邻域中去掉a的数的 集合，应用于高等数学)所有点的函数值满足不等式 |𝑓(𝑥)−𝐴|<𝜀 。这就是“在 𝑥→𝑥0 的过程中，对应函数值 𝑓(𝑥) 无限接近于确定的常数 𝐴”的实质。

2.函数极限定义之精确定义:( 𝜀−𝛿 语言)：

设 𝑓(𝑥) 在点 𝑥₀ 的某个去心邻域内有定义，如果对于任意给定的正数 𝜀 ，总存在一个正数 𝛿 ，使对于适合不等式 0<|𝑥−𝑥₀|<𝛿 的一切 𝑥 ，对应的函数值 𝑓(𝑥) 满足 |𝑓(𝑥)−𝐴|<𝜀 ，那么称常数 𝐴 为函数 𝑓(𝑥) 当 𝑥→𝑥₀ 时的极限，记作

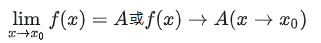
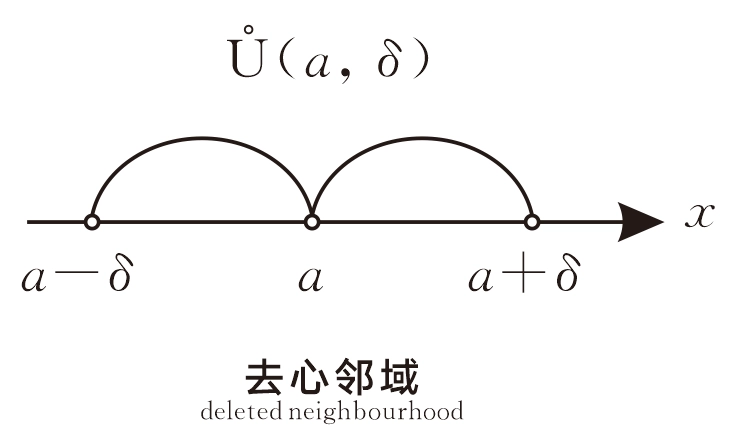
注：(1)定义中 |𝑥−𝑥₀|>0 表示 𝑥≠𝑥₀ ,所以即使 𝑓(𝑥) 在 𝑥₀ 没有定义， 𝑓(𝑥₀) 在 𝑥₀ 点也可以有极限。因为我们研究极限是研究 𝑥→𝑥₀ 过程中 𝑓(𝑥) 的变化趋势，而与 𝑓(𝑥) 在 𝑥₀ 处有无定义没有关系。

(2) 𝛿 的取值与 𝜀 有关，且 𝛿 不唯一。也就是说，任意给一个 𝜀 就会有一个 𝛿 与之对应，换一个 𝜀 就换一个 𝛿 ，这一点和数列极限中的 𝑁 是一样的。

 (3) lim𝑥→𝑥0𝑓(𝑥)=𝐴 的几何解释：|𝑓(𝑥)−𝐴|<𝜀等价于 𝐴−𝜀<𝑓(𝑥)<𝐴+𝜀 。对于任意给定的 𝜀>0 ，存在 𝑥₀ 的 𝛿 去心邻域 𝑈˚(𝑥₀,𝛿) ，当 𝑦=𝑓(𝑥) 图像上的点横坐标落在𝑥₀ 的 𝛿 去心邻域 𝑈˚(𝑥0,𝛿) 内，这些点的纵坐标满足𝐴−𝜀<𝑓(𝑥)<𝐴+𝜀。即这些点落在下图中的红色虚线矩形框内：

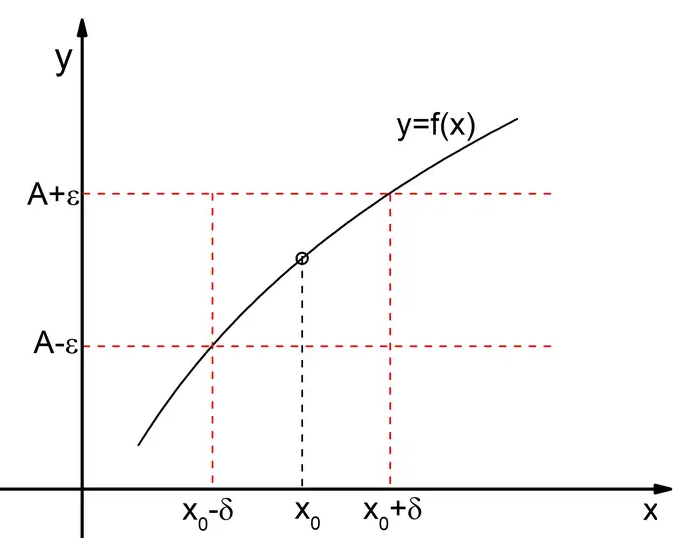
利用极限的定义证明函数的极限：

3.极限的局部保号性定理

定理1：如果 lim_𝑥→𝑥0𝑓(𝑥)=𝐴 ，且 𝐴>0(𝐴<0) ，那么存在 𝑥₀ 的去心邻域，当 𝑥 在该邻域时，有 𝑓(𝑥)>0(𝑓(𝑥)<0) 。

证明：因为lim_𝑥→𝑥0𝑓(𝑥)=𝐴 ，且 𝐴>0 ，根据极限的定义中 𝜀 的任意性，仅仅针对此问题而言，我们不妨特意给定一个 𝜀 它满足 0<𝜀<𝐴 ，那么肯定会存在一个相应的 𝑥₀ 的去心邻域 𝑈˚(𝑥₀,𝛿) ，使当 0<|𝑥−𝑥₀|<𝛿 时， |𝑓(𝑥)−𝐴|<𝜀 ，即 𝐴−𝜀<𝑓(𝑥)<𝐴+𝜀 ①，又因为我们给定的 𝜀 满足 0<𝜀<𝐴，结合不等式①的左侧可知 𝑓(𝑥)>𝐴−𝜀>0 。证毕！

定理1':如果 lim_𝑥→𝑥0𝑓(𝑥)=𝐴 (𝐴≠0) ，那么必存在 𝑥₀ 的某去心邻域，当 𝑥 在该邻域时，有 |𝑓(𝑥)|>|𝐴|/2 。

证明：因为 lim_𝑥→𝑥0𝑓(𝑥)=𝐴 ，根据函数极限的定义，对给定 𝜀0=|𝐴|/2>0 ，必然有 𝛿>0 ，使当 0<|𝑥−𝑥₀|<𝛿 时， |𝑓(𝑥)−𝐴|<𝜀₀ ，由绝对值不等式的特点，可以进一步有 ||𝑓(𝑥)|−|𝐴||≤|𝑓(𝑥)−𝐴|<𝜀₀ ，所以 |𝑓(𝑥)|>|𝐴|−𝜀₀=|𝐴|−|𝐴|/2=|𝐴|/2 。证毕！

定理2：如果在 𝑥₀ 的某个去心邻域内 𝑓(𝑥)≥0(𝑓(𝑥)≤0) ，而且 lim_𝑥→𝑥0𝑓(𝑥)=𝐴 ，那么 𝐴≥0(𝐴≤0) 。

该定理的证明需要利用定理1的结论。下面我们来证明，

证明(反证法)：存在 𝑥0 的某个去心邻域，使该邻域内 𝑓(𝑥)≥0 ，则极限值 𝐴≥0 。若不然，假设 𝐴<0 ，根据定理1，存在 𝑥₀ 的某个去心邻域，使当 𝑥 在该邻域内时， 𝑓(𝑥)<0 ，这与题设矛盾。证毕！

定理1和定理2都叫函数极限的局部保号性定理，这个定理在今后推导其它定理时是非常有用的，所以还请重视！

4.单侧极限

写在前面的话：我们需要知道当 𝑥→𝑥₀ ， 𝑓(𝑥) 趋近于某个常数时， 𝑥 可以从左侧趋近于 𝑥₀ ，也可以从右侧趋近于 𝑥₀ ，所以我们有必要讨论一下函数 𝑓(𝑥) 的单侧极限的定义：

如果对任给的 𝜀>0 ，总存在 𝛿>0 ，当 𝑥₀−𝛿<𝑥<𝑥0 时， |𝑓(𝑥)−𝐴|<𝜀 ，那么称 𝐴 为 𝑓(𝑥) 当 𝑥→𝑥₀ 时的左极限，

记作 或lim_{𝑥→𝑥0−}𝑓(𝑥)=𝐴或𝑓(𝑥₀−0)=𝐴 。

如果对任给的 𝜀>0 ，总存在 𝛿>0 ，当 𝑥0<𝑥<𝑥0+𝛿 时， |𝑓(𝑥)−𝐴|<𝜀 ，那么称 𝐴 为 𝑓(𝑥) 当 𝑥→𝑥0 时的右极限，

记作 或lim_{𝑥→𝑥0+}𝑓(𝑥)=𝐴或𝑓(𝑥₀+0)=𝐴 。

函数极限与单侧极限的关系：当 𝑥→𝑥0 时，函数 𝑓(𝑥) 极限存在的充分必要条件是函数 𝑓(𝑥) 左极限、右极限都存在并且相等。

二、自变量趋近于无穷大时函数的极限

首先我们先搞清楚如下两个问题：

𝑥 趋近于无穷大： 𝑥→∞ ,指 |𝑥| 无限增大。

lim_𝑥→∞𝑓(𝑥)=𝐴 ：是指当|𝑥| 无限增大时， 𝑓(𝑥) 无限接近于 𝐴 。

这样我们就很容易理解自变量趋近于无穷大时函数极限的定义了，如下：

定义：设函数 𝑓(𝑥) 当 |𝑥| 大于某一正数时有定义。如果对于任意给定的正数 𝜀 ,总存在正数 𝑋 ，使当 |𝑥|>𝑋 时，不等式 |𝑓(𝑥)−𝐴|<𝜀 恒成立，则称 𝐴 为 𝑓(𝑥) 当 𝑥→∞ 时的极限，记作 或lim𝑥→∞𝑓(𝑥)=𝐴或𝑓(𝑥)→𝐴(𝑥→∞) 。 

 同样，自变量趋近于无穷大时函数的单侧极限定义如下：

lim_{𝑥→−∞}𝑓(𝑥)=𝐴 定义为：如果对于任意给定的正数 𝜀 ,总存在正数 𝑋 ，使当 𝑥<−𝑋 时，不等式 |𝑓(𝑥)−𝐴|<𝜀 恒成立，则称 𝐴 为 𝑓(𝑥) 当 𝑥→−∞ 时的极限。

lim_𝑥→+∞𝑓(𝑥)=𝐴 定义为：如果对于任意给定的正数 𝜀 ,总存在正数 𝑋 ，使当 𝑥>𝑋 时，不等式 |𝑓(𝑥)−𝐴|<𝜀 恒成立，则称 𝐴 为 𝑓(𝑥) 当 𝑥→+∞ 时的极限。

注：

①值得一提的是 lim_𝑥→∞𝑓(𝑥)=𝐴 的充分必要条件是 lim_{𝑥→−∞}𝑓(𝑥)=lim_𝑥→+∞𝑓(𝑥)=𝐴 。

②lim_𝑥→∞𝑓(𝑥)=𝐴的几何解释为：对任给的 𝜀>0 ，总存在正数 𝑋 ，使当 或𝑥>𝑋或𝑥<−𝑋 时， 𝑦=𝑓(𝑥) 的图像位于直线 𝑦=𝐴−𝜀 与 𝑦=𝐴+𝜀 之间。