容斥原理以及Nim基础（异或，SG函数）

容斥原理：

容斥的复杂度为O（2^m)，所以可以通过，对于实现，一共2^n-1种，我们可以用二进制来实现

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=20;
int n,m;
int p[N];
int main()
{
    cin>>n>>m;
    for(int i=0;i<m;i++) cin>>p[i];
    int res=0;
    for(int i=1;i<1<<m;i++)
    {
        int t=1,cnt=0;
        for(int j=0;j<m;j++)
        {
            if(i>>j&1)
            {
                cnt++;
                if((LL)t*p[j]>n)
                {
                    t=-1;
                    break;
                }
                t*=p[j];
            }
        }
        if(t!=-1)
        {
            if(cnt%2) res+=n/t;
            else res-=n/t;
        }
    }
    cout<<res;
}

博弈论：

先手必胜状态：可以走到某一个必败状态。

先手必败状态：可以走到任何一个必胜状态。

异或是0就是先手必败，反之必胜。

等价于证a1^a2^...=x!=0，走一步使其变成0

找到x的最高k位1，那么ai中第k位1，那么ai^x<ai，我们从ai拿走ai-(a1^x)个即可。

这样子，假如第一个人！=0,那么下一个人一定是0，那么它又不是0，而一个人败即0^0..=0，因此第一个人一定不会败，即必胜。

sg函数：

首先定义mex(S)表示不属于S的最小非负整数即mex(S)=min(x),x属于自然数并且不属于S

SG函数：

一个状态可以走到不同的状态，这样就形成了有向图，我们令终点为0，SG(终点(即没有出边）)=0,假如当前X局面可以通过k个操作变成y1,...yk,那么SG（x)=mex{SG(y1),...SG(yk)}

SG(x)=0:必败,!=0:必胜

因为!=0，那么X可以到0，=0的就到不了0，这样子先手！=0就可以保证自己一定不是0，而终点一定是0，那么先手必胜。

实际情况中可能有不止1个图，每一次可以从其中一个走一步，因此答案就是SG(X1)^SG(X2)...

Xi表示每一个图的起始状态

证明类似与Nim游戏

终点：所有终点SG=0，为0

若其不是0，那么一定存在使其变成0的方案（由mex性质）

假如只有一堆10并只可以选2和5我们可以画出下面的状态图：

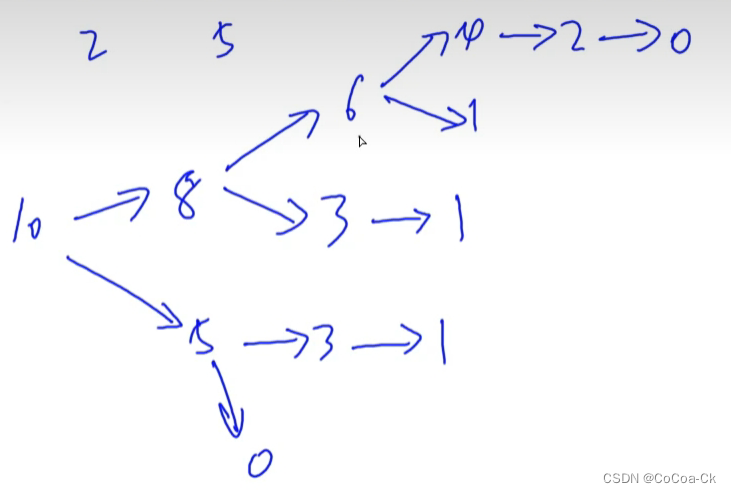
下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
const int N=110,M=10010;
int n,m;
int s[N],f[M];
int res;
int sg(int x)//记忆化搜素
{
    if(f[x]!=-1) return f[x];
    unordered_set<int> S;
    for(int i=0;i<m;i++)
    {
        int sum=s[i];
        if (x >= sum) S.insert(sg(x - sum));
    }
    for (int i = 0; ; i ++ )
        if (!S.count(i))
            return f[x] = i;
}
int main()
{
    cin>>m;
    for(int i=0;i<m;i++) cin>>s[i];
    cin>>n;
    memset(f,-1,sizeof(f));//sg是唯一的，因为就算不同图，当前值一样并且可以的操作也一样。
    for(int i=0;i<n;i++)
    {
        int x;
        cin>>x;
        res^=sg(x);
    }
    if(res) cout<<"Yes";
    else cout<<"No";
}

Nim的几个变种：

对于样例，先手把3拿一个给2，变成2，2，2

若对手拿的是第二台阶的，那么它就把相应的放到地面，这样子1和3个数就不变。

若从3拿1给2，我们就从1拿1个给地面，因此对于我们来说，1，3的个数都不一致，而对手都一致，最终都为0，因此先手必胜。

因此，对于一般情况，我们看奇数台阶：

a1^a3^...=x!=0那么先手必胜，反之必败

类似上面的SG函数，不过这里注意SG（b1,b2)=SG(b1)^SG(b2)

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int f[N];
int sg(int x)
{
    if(f[x]!=-1) return f[x];
    unordered_set<int> S;
    for(int i=0;i<x;i++){
        for(int j=0;j<=i;j++)
        {
            S.insert(sg(i)^sg(j));
        }
    }
    for(int i=0;;i++)
    {
        if(!S.count(i)) return f[x]=i;
    }
}
int main()
{
    int n;
    cin>>n;
    memset(f,-1,sizeof(f));
    int res=0;
    for(int i=0;i<n;i++)
    {
        int x;
        cin>>x;
        res^=sg(x);
    }
    if(res) cout<<"Yes";
    else cout<<"No";
}