传统流程图和N-S流程图的区别

CyberMuse

已于 2024-10-08 16:45:26 修改

阅读量1.4k

点赞数 9

文章标签：数据结构

于 2024-10-07 09:09:59 首次发布

本文链接：https://blog.csdn.net/cocofu/article/details/142734907

版权

传统流程图和N-S流程图在表示算法和逻辑结构时有不同的特点和用途。以下是它们的主要区别：

### 传统流程图

1. **符号多样**：传统流程图使用多种几何形状表示不同的操作类型，如椭圆表示开始和结束，平行四边形表示输入输出，矩形表示处理步骤，菱形表示决策等。

2. **流动性**：通过箭头连接各个符号，表示执行流程的方向和顺序。

3. **直观性**：适合展示复杂的流程，尤其是有多个分支和决策的情况下，每个步骤的执行顺序一目了然。

4. **灵活性**：可以在图中自由地添加和连接不同的操作符号，适合展示复杂的逻辑结构。

### N-S流程图 (Nassi-Shneiderman图)

1. **结构化**：N-S流程图使用嵌套的矩形块来表示程序结构，强调结构化编程理念，每个块代表一个控制结构（如顺序、选择、循环）。

2. **无箭头**：没有箭头，控制流程通过块的嵌套和顺序来表示，避免了箭头可能引起的混乱。

3. **清晰性**：由于其结构化特性，N-S流程图更容易体现程序的逻辑结构，特别是在有嵌套循环和条件的情况下。

4. **模块化**：适合于模块化设计，易于分解和理解复杂的算法。

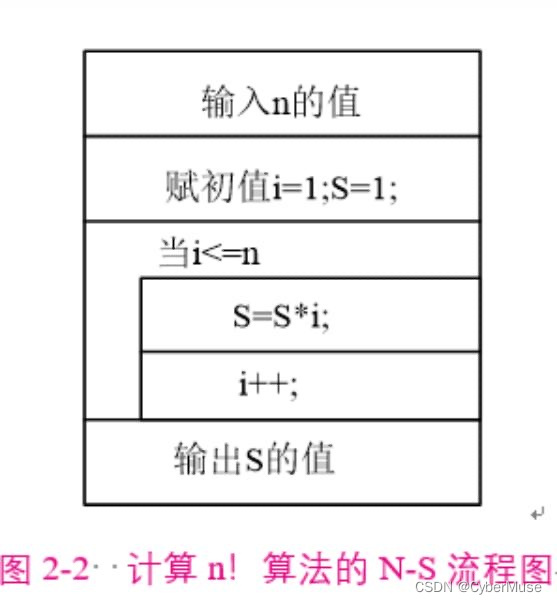
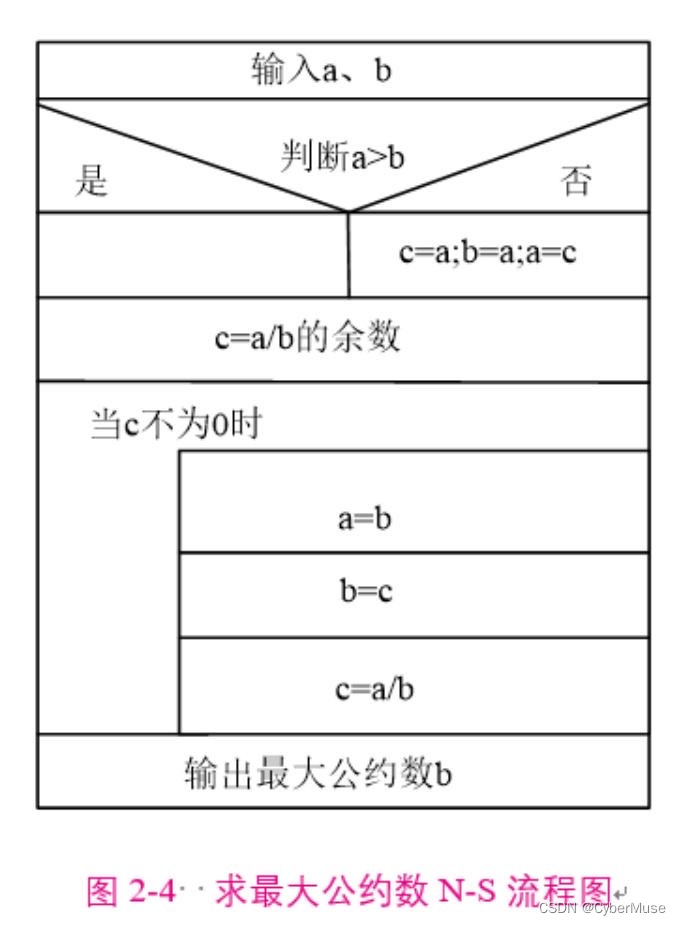
### 总结

- **传统流程图**更适合于直观地展示流程的每一个细节和分支情况，适用于需要详细展示流程各个步骤的场合。

- **N-S流程图**则更适合于展示程序的结构化逻辑，强调代码的结构性和模块化，适合于程序设计和理解。

两者各有优劣，选择使用哪种图表通常取决于具体的应用场景和个人偏好。

～～～

今天我们来学习如何用流程图来解决两个有趣的问题。一个是找出1990到2016年之间的所有闰年，另一个是找出两个数字之间的所有素数。我们会用两种不同的流程图来表示这些算法，分别是传统流程图和N-S流程图。

### 什么是流程图？

流程图就像是一个图画，帮助我们一步一步地解决问题。它用各种形状和箭头来表示做事情的顺序。比如，开始和结束通常用椭圆形表示，做某件事情用矩形表示，问一个问题用菱形表示。

### 闰年的算法

#### 什么是闰年？

闰年是为了让我们的日历和地球绕太阳转的时间保持一致的一种方法。简单来说，闰年有两个条件：
1. 年份能被4整除，但不能被100整除。
2. 或者年份能被400整除。

### 为什么要闰年？

地球绕太阳一圈大约需要365.24天，而我们的日历一年只有365天。为了弥补这0.24天的差距，我们每四年增加一天，这就是2月29日，称为闰年。这样做可以让我们的日历年和太阳年更加吻合。

### 闰年的两个条件

1. **年份能被4整除，但不能被100整除**：
- **被4整除**：因为0.24天乘以4大约等于1天，所以每四年加一天就能补上这些额外的时间。
- **不能被100整除**：如果年份能被100整除，比如1900年，这一年虽然按每四年加一天的规则应是闰年，但实际上不是。原因是这些年累积的误差需要调整，因为在400年周期内，单单每四年加一天会多出一些时间。

2. **年份能被400整除**：
- **被400整除**：为了进一步调整误差，每400年再加一天。这样一来，公历就更精确了。因此，像2000年就是闰年，因为它能被400整除。

### 总结

这些规则综合考虑了地球绕太阳公转时间和日历年的差异，使得我们的日历与地球的实际运行情况更加一致。这也是为什么有时年份能被4整除但不是闰年（例如，1900年），而能被400整除的一定是闰年（例如，2000年）。希望这个解释能帮助你理解这些规则的由来！如果还有其他问题，欢迎继续提问哦！

#### 如何用流程图找闰年？

1. **开始**：我们从1990年开始。
2. **检查年份**：看看这个年份是不是在我们想要的范围内（1990到2016）。
3. **判断闰年**：检查这个年份是不是闰年。我们用条件1和条件2来判断。
4. **输出结果**：如果是闰年，就把这个年份记下来。
5. **继续下一个年份**：把年份加1，然后重复检查，直到2016。
6. **结束**：当我们检查完2016年，就结束了。

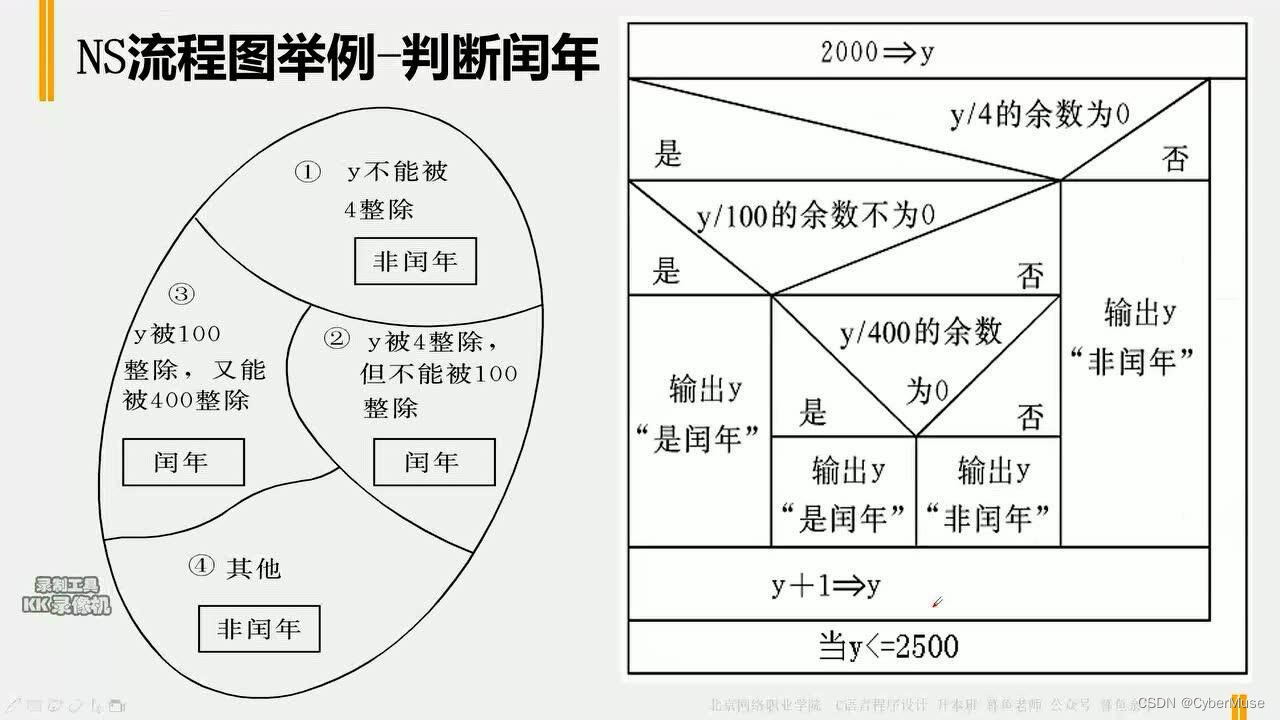
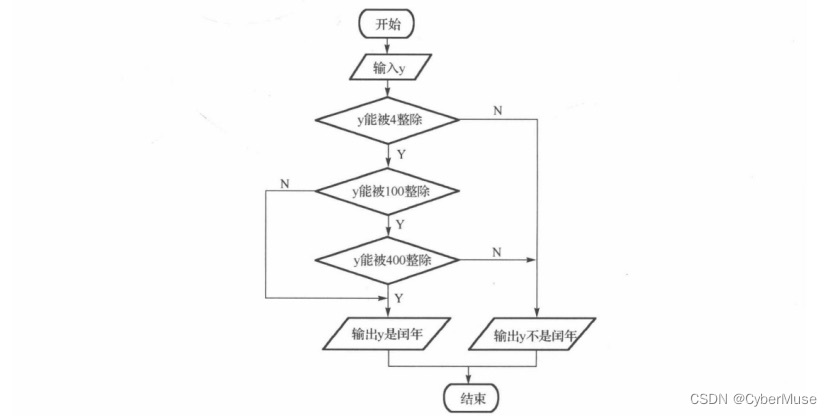
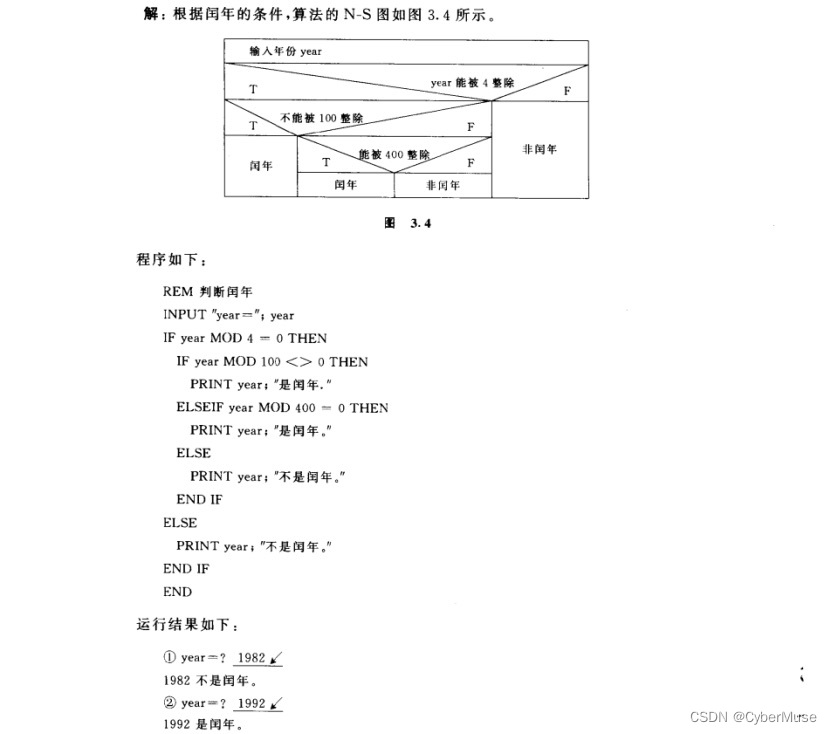
### 闰年算法流程图

#### 传统流程图

1. **开始节点**：画一个椭圆形标记“开始”。
2. **初始化年份**：画一个矩形，写上“year = 1990”。
3. **检查年份上限**：画一个菱形，写上“year <= 2016?”。
- **是**：指向下一步。
- **否**：指向结束节点。
4. **闰年条件检查**：画一个菱形，写上“(year % 4 == 0 AND year % 100 != 0) OR (year % 400 == 0)?”。
- **是**：画一个矩形，写上“输出 year”。
5. **年份增加**：画一个矩形，写上“year = year + 1”。
6. **返回步骤 3**：用箭头指回到“检查年份上限”。
7. **结束节点**：画一个椭圆形标记“结束”。

#### N-S流程图

1. **开始块**：画一个长方形，写上“开始”。
2. **初始化**：画一个长方形，写上“year = 1990”。
3. **循环结构**：画一个长方形，写上“WHILE year <= 2016 DO”。
- **条件**：在循环内部画一个长方形，写上“IF (year % 4 == 0 AND year % 100 != 0) OR (year % 400 == 0) THEN”。
- 在条件内画一个长方形，写上“输出 year”。
- **年份增加**：画一个长方形，写上“year = year + 1”。
4. **结束块**：画一个长方形，写上“结束”。

### 素数的算法

#### 什么是素数？

素数是只能被1和它本身整除的数，比如2、3、5、7等等。

好的，让我们来深入了解一下为什么只需要检查一个数能否被小于等于其平方根的数整除就可以判断它是否是素数。

### 理论背景

假设我们有一个整数 \( n \)，如果 \( n \) 不是素数，那么它可以写成两个因数的乘积：\( n = a \times b \)，其中 \( a \) 和 \( b \) 都大于 1。

为了证明这一点，我们假设 \( a \leq b \)。那么，根据乘积的性质，\( a \times a \leq a \times b = n \)。这意味着 \( a \leq \sqrt{n} \)。

### 证明过程

1. **假设 \( n \) 不是素数**：如果 \( n \) 不是素数，那么它至少可以分解为两个因数 \( a \) 和 \( b \)，即 \( n = a \times b \)。

2. **假设 \( a \leq b \)**：我们可以假设 \( a \) 是较小的因数（如果 \( a > b \)，我们可以交换 \( a \) 和 \( b \)），因此有 \( a \leq \sqrt{n} \)。

3. **结论**：如果 \( n \) 能被某个数整除，那么它至少可以被一个小于或等于 \( \sqrt{n} \) 的数整除。这是因为如果 \( a > \sqrt{n} \)，那么 \( b \) 必须小于 \( \sqrt{n} \) 以使得 \( a \times b = n \) 成立。

### 例子说明

- **例如，检查 36 是否为素数**：
- 36 可以分解为 \( 6 \times 6 \) 或 \( 4 \times 9 \) 等。
- 其平方根是 6。我们可以看到，36 可以被小于或等于 6 的数（如 2、3、4、6）整除。

- **再看 29**：
- 29 的平方根约为 5.38，因此我们只需检查 2、3、4、5。
- 29 不能被这些数整除，所以 29 是素数。

### 总结

通过这个推理，我们知道，在判断一个数 \( n \) 是否为素数时，只需要检查从 2 到 \( \sqrt{n} \) 的数是否能整除 \( n \)。如果没有一个数能整除它，那么 \( n \) 就是素数。这种方法大大减少了需要检查的数目，使得判断是否为素数的过程更加高效。

当然可以！让我们用简单易懂的方式来找出两个数之间的所有素数。假设我们有两个整数 X 和 Y，并且 X 小于或等于 Y。我们要做的是找出 X 和 Y 之间的所有素数。素数是指只能被 1 和它本身整除的数。那么，我们如何来找出这些素数呢？

找素数：

### 第一步：输入验证

首先，我们需要确保输入的两个数是正确的，并且 X 应该小于或等于 Y。这样我们的问题才有意义。

### 第二步：从 X 到 Y 检查每个数

接下来，我们要做的是从 X 到 Y，一个一个地检查这些数字，看看它们是否是素数。我们要用一个简单的方法来判断一个数是不是素数。

### 第三步：判断一个数是否为素数

对于每个数字 n，我们需要判断它是否是素数。以下是简单的步骤：

1. **排除 1 和小于 1 的数**：1 不是素数，因为素数必须大于 1。

2. **检查 2**：2 是唯一的偶数素数。如果 n 是 2，那么它就是素数。

3. **排除偶数**：如果 n 大于 2 并且是偶数，那么它不是素数，因为偶数都能被 2 整除。

4. **检查奇数**：对于大于 2 的奇数，我们需要检查它是否能被小于它的某个数整除。如果不能被任何数整除，那么它就是素数。

- 具体来说，我们只需要检查能否被小于等于它平方根的数整除。为什么呢？因为如果 n 能被一个大于其平方根的数整除，那么 n 也能被一个小于其平方根的数整除。

### 第四步：用一个例子来说明

假设 X 是 10，Y 是 20，我们来找出 10 到 20 之间的素数：

- **检查 10**：10 是偶数，不是素数。
- **检查 11**：11 不能被 2、3整除，所以 11 是素数。
- **检查 12**：12 是偶数，不是素数。
- **检查 13**：13 不能被 2、3整除，所以 13 是素数。
- **检查 14**：14 是偶数，不是素数。
- **检查 15**：15 能被 3 整除，不是素数。
- **检查 16**：16 是偶数，不是素数。
- **检查 17**：17 不能被 2、3、4 整除，所以 17 是素数。
- **检查 18**：18 是偶数，不是素数。
- **检查 19**：19 不能被 2、3、4 整除，所以 19 是素数。
- **检查 20**：20 是偶数，不是素数。

所以，10 到 20 之间的素数是 11、13、17 和 19。

### 第五步：总结

通过以上步骤，我们学习了如何找出两个数之间的所有素数。这个方法简单而有效，让我们可以轻松判断一个数是不是素数。这样的技巧对我们理解数字和数学规律非常有用。

#### 如何用流程图找素数？

使用流程图来找素数是一种直观的方法，可以清晰地展示判断一个数是否为素数的步骤。下面，我们将绘制一个简单的流程图步骤来帮助理解这个过程。

### 步骤说明

1. **开始**：流程从开始节点开始。

2. **输入数字 \( n \)**：输入需要检查的数字。

3. **检查 \( n \) 是否小于等于 1**：
- 如果是，输出 "不是素数"，然后结束。
- 如果不是，继续下一步。

4. **检查 \( n \) 是否等于 2**：
- 如果是，输出 "是素数"，然后结束。
- 如果不是，继续下一步。

5. **检查 \( n \) 是否为偶数**（即 \( n \mod 2 = 0 \)）：
- 如果是，输出 "不是素数"，然后结束。
- 如果不是，继续下一步。

6. **初始化变量 \( i = 3 \)**：从 3 开始检查，因为 2 已经排除。

7. **检查 \( i \times i \leq n \)**：
- 如果 \( i \times i > n \)，输出 "是素数"，然后结束。
- 如果 \( i \times i \leq n \)，继续下一步。

8. **检查 \( n \mod i = 0 \)**：
- 如果是，输出 "不是素数"，然后结束。
- 如果不是，继续下一步。

9. **增加 \( i \) 的值**：将 \( i \) 增加 2（因为偶数已经被排除了，所以只检查奇数）。

10. **返回到步骤 7**：重复检查，直到确定 \( i \times i > n \) 或找到一个因数。

### 流程图概念

虽然这里文字描述比较多，但一个流程图的基本形状可以这样概括：

```
开始
↓
输入 n
↓
n ≤ 1 吗？——是——> 输出 "不是素数" ——> 结束
↓否
n = 2 吗？——是——> 输出 "是素数" ——> 结束
↓否
n 是偶数吗？——是——> 输出 "不是素数" ——> 结束
↓否
初始化 i = 3
↓
i × i ≤ n 吗？
↓
是
↓否
n 能被 i 整除吗？——是——> 输出 "不是素数" ——> 结束
↓否
i = i + 2
↓
返回到检查 i × i ≤ n
```

当然，我会逐步引导你如何绘制传统流程图和N-S流程图来表示从X到Y之间找素数的算法。

### 传统流程图绘制步骤

1. **开始**：绘制一个椭圆形，写上“开始”。

2. **输入X和Y**：使用平行四边形表示输入操作，写上“输入X, Y”。

3. **初始化n = X**：使用矩形表示处理步骤，写上“n = X”。

4. **检查n是否大于Y**：使用菱形表示决策，写上“n > Y?”。
- **是**：箭头指向“结束”。
- **否**：箭头指向下一步骤。

5. **检查n是否为素数**：
- **n <= 1**：用菱形表示，写上“n <= 1?”。如果是，箭头指向增加n。
- **n = 2**：用菱形表示，写上“n = 2?”。如果是，箭头指向输出n。
- **n是偶数且大于2**：用菱形表示，写上“n为偶数?”。如果是，箭头指向增加n。

6. **检查因子**：从i = 3到sqrt(n)，用循环表示。
- **能否被i整除**：用菱形表示，写上“n mod i == 0?”。如果是，箭头指向增加n。

7. **输出n**：用平行四边形表示，写上“输出n”。

8. **增加n的值**：用矩形表示，写上“n = n + 1”，箭头返回到检查n是否大于Y。

9. **结束**：绘制一个椭圆形，写上“结束”。

### N-S流程图绘制步骤

1. **开始**：在顶部写上“开始”。

2. **输入X和Y**：在下一行写上“输入X, Y”。

3. **循环结构**：画一个大的矩形框，标记为“循环n从X到Y”。

- **判断n是否大于1**：在框内的第一行写上“如果n > 1”，接下来是“否则，跳过”，下一个分支是“继续”。

- **判断n是否等于2**：写上“如果n = 2，输出n”。

- **判断n是否为偶数且大于2**：写上“如果n为偶数且>2，跳过”。

- **因子检查循环**：在框内再画一个小的循环框，标记为“从i = 3到sqrt(n)”。

- **能否被i整除**：写上“如果n mod i == 0，跳过”。

- **如果没有找到因子**：写上“输出n”。

4. **结束**：在框的最后一行写上“结束”。

### 图示化总结

通过这两个流程图，你可以清楚地可视化算法的逻辑流程。传统流程图使用形状和箭头展示决策、处理和输入输出，而N-S流程图通过嵌套矩形结构展示程序逻辑。这两种方法都可以帮助理清复杂的逻辑步骤，便于理解和实现。

如果你需要详细的图示或有其他问题，请随时告诉我！

### 总结

这种方式让我们清晰地看到每一步的逻辑决策过程。流程图的优势在于它的直观性，使得判断条件和逻辑流转一目了然。希望这个说明能帮助你理解如何使用流程图来找素数！如果需要更多帮助或者有疑问，请随时告诉我。

这些步骤可以帮助你使用工具绘制流程图。可以考虑使用Lucidchart、Visio、Draw.io或其他流程图软件来实现这些设计。希望这能帮助你创建准确的流程图！

【注】

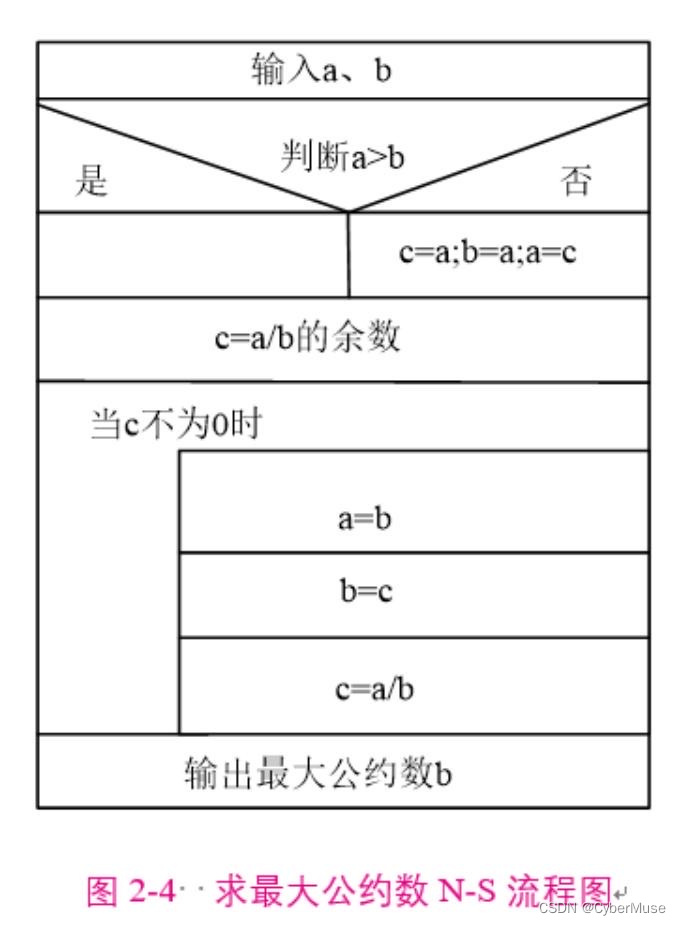
### 什么是最大公约数？

想象一下，你有两堆糖果，一堆有12颗，另一堆有8颗。你想把这两堆糖果分成一样大小的小组，每组里有相同数量的糖果，而且不能剩下任何糖果。我们要找的就是可以让这两堆糖果都平均分开的最大的小组数。这个最大的小组数就是所谓的“最大公约数”。

### 怎么找到最大公约数？

我们可以用一个简单的方法来找到最大公约数，叫做“列举法”。让我们来看一下步骤：

1. **列举因数**：首先，我们要找出这两个数字（12和8）的所有因数。因数就是能整除这个数字的数。

- 12的因数有：1, 2, 3, 4, 6, 12
- 8的因数有：1, 2, 4, 8

2. **找共同的因数**：接下来，我们看看这两个数字有哪些因数是相同的，也就是共同因数。

- 12和8的共同因数有：1, 2, 4

3. **找最大值**：最后，从共同因数中找出最大的那个数，这个数就是最大公约数。

- 最大的共同因数是4，所以12和8的最大公约数是4。

### 为什么最大公约数很有用？

最大公约数在生活中有很多有趣的应用。比如：

- **简化分数**：如果你有一个分数，比如12/8，你可以用最大公约数来把它简化。因为12和8的最大公约数是4，你可以把分子和分母都除以4，这样12/8就变成了3/2。

- **做游戏**：如果你有很多小玩具，想要公平地分给小伙伴们，你可以用最大公约数来确保每个人都得到同样多的玩具。

- **排队问题**：有时候，老师想让同学们排成队，比如每排有相同人数。用最大公约数，我们可以很容易知道最多能排成几队。

### 用一个游戏来理解最大公约数

让我们玩一个小游戏，帮助你更好地理解最大公约数。

假设你有18个苹果和24个橘子。你想把它们放到盒子里，每个盒子里的苹果和橘子数目都相同，而且不剩下任何水果。那么你需要多少个盒子呢？这就是在找18和24的最大公约数。

1. **找因数**：
- 18的因数有：1, 2, 3, 6, 9, 18
- 24的因数有：1, 2, 3, 4, 6, 8, 12, 24

2. **找共同的因数**：
- 共同因数有：1, 2, 3, 6

3. **找最大值**：
- 最大的共同因数是6，所以18和24的最大公约数是6。

这意味着你可以用6个盒子来装这些水果，每个盒子里放3个苹果和4个橘子。

### 总结

最大公约数就是找出两个数可以被同样整除的最大数。通过找出共同因数并选出最大的那个，我们就能找到最大公约数。它在很多情况下都很有帮助，比如简化分数、分配物品等。

最大公约数的英文全称是 "Greatest Common Divisor"，通常缩写为 GCD。

求解两个整数的最大公约数（GCD）最常用的算法是**欧几里得算法**。这个算法通过反复取余来简化问题，直到找到最大公约数。以下是欧几里得算法的步骤和一些示例代码：

### 欧几里得算法步骤

1. **初始化**：给定两个整数a和b。
2. **判断b是否为0**：
- 如果b是0，则a就是两个数的最大公约数（GCD）。
- 如果b不是0，则继续到下一步。
3. **计算余数**：计算a除以b的余数r（即r = a % b）。
4. **替换变量**：将a替换为b，将b替换为r。
5. **重复步骤2**：循环执行步骤2到4，直到b为0。
6. **结果**：当b为0时，当前的a就是GCD。

### 示例代码

下面是Python中实现欧几里得算法的代码示例：

```python
def gcd(a, b):
while b != 0:
a, b = b, a % b
return a

# 示例使用
print(gcd(48, 18)) # 输出：6
```

### 说明

- **效率**：欧几里得算法非常高效，能够快速求出两个数的最大公约数，即便是大数也能在短时间内完成。
- **递归实现**：该算法也可以通过递归方式实现，逻辑相同，只是通过函数自身调用来实现循环：

```python
def gcd_recursive(a, b):
if b == 0:
return a
else:
return gcd_recursive(b, a % b)

# 示例使用
print(gcd_recursive(48, 18)) # 输出：6
```

求解最大公约数（GCD）的数学基础主要涉及几个基本概念和性质：

### 数学定义

1. **整除**：如果整数 \( a \) 能被整数 \( b \) 整除，即存在整数 \( k \) 使得 \( a = bk \)，则称 \( b \) 是 \( a \) 的因数。

2. **公约数**：给定两个整数 \( a \) 和 \( b \)，同时是 \( a \) 和 \( b \) 的因数的整数称为 \( a \) 和 \( b \) 的公约数。

3. **最大公约数**：在所有公约数中，最大的那个数就是 \( a \) 和 \( b \) 的最大公约数，记作 \(\text{GCD}(a, b)\)。

### 性质

1. **性质1**：如果 \( b \neq 0 \)，则 \(\text{GCD}(a, b) = \text{GCD}(b, a \mod b)\)。这是欧几里得算法的基础。

2. **性质2**：如果 \( a \) 和 \( b \) 的最大公约数是 \( d \)，则存在整数 \( x \) 和 \( y \) 使得 \( ax + by = d \)。这个性质来源于贝祖定理。

3. **性质3**：若 \( a \) 是 \( b \) 的倍数，则 \(\text{GCD}(a, b) = b\)。

### 欧几里得算法

欧几里得算法是基于性质1，通过不断用较小的数去除较大的数，最终将问题简化到一个较小的问题。具体步骤已经在前面回答中解释过。

### 应用

1. **简化分数**：通过求分子和分母的GCD，可以将分数化为最简形式。
2. **数论问题**：GCD在很多数论问题中都有应用，如求解二次同余方程。
3. **密码学**：在RSA等加密算法中，GCD用于计算模反元素。

这些数学基础和性质构成了理解和计算最大公约数的核心。

证明：

【注2】

埃拉托色尼筛法（Sieve of Eratosthenes）是一种经典的用于找出一段范围内所有素数的高效算法。它的数学原理和证明主要基于素数的定义和倍数的性质。

### 数学原理

1. **素数的定义**：
- 素数是指大于 1 且仅能被 1 和其自身整除的整数。

2. **倍数性质**：
- 如果一个数 \(n\) 是合数，则它至少有一个因子 \(p\)，其中 \(2 \leq p \leq \sqrt{n}\)。
- 因此，对于一个合数 \(n\)，其最小素因子一定小于或等于 \(\sqrt{n}\)。

3. **算法思想**：
- 从最小的素数 2 开始，标记它的所有倍数为合数。
- 找到下一个未标记的数，它即为下一个素数。
- 重复上述步骤直到标记到最大需要检查的数为 \(\sqrt{Y}\)。

### 算法证明

埃拉托色尼筛法的正确性可以通过以下几点来证明：

1. **初始条件**：
- 所有数从 2 到 \(Y\) 都被假设为素数。

2. **倍数标记**：
- 当一个素数 \(p\) 被发现时，所有大于或等于 \(p^2\) 的 \(p\) 的倍数都被标记为合数。
- 这是因为小于 \(p^2\) 的 \(p\) 的倍数要么已经被标记（由于更小的素数），要么不在考虑范围内。

3. **算法终止**：
- 当 \(p\) 超过 \(\sqrt{Y}\) 时，所有合数都已经被标记，因为任何合数 \(n\) 必定有一个小于或等于 \(\sqrt{n}\) 的素因子。

4. **未标记数为素数**：
- 在算法结束后，所有未被标记的数即为素数，因为它们没有更小的素因子。

通过以上步骤，埃拉托色尼筛法能够有效地找出范围内的所有素数，其时间复杂度约为 \(O(n \log \log n)\)，其中 \(n\) 是范围的上限，这使其在处理大范围素数查找时非常高效。

这种算法的效率和简单性使其成为计算机科学和数学中处理素数问题的一个重要工具。

当然可以！除了基本的素数检测方法，我们还可以使用埃拉托色尼筛法（Sieve of Eratosthenes）来找出某个范围内的所有素数。埃拉托色尼筛法是一种高效的算法，特别适合用于找出较大范围内的素数。

### 埃拉托色尼筛法算法

埃拉托色尼筛法的基本思想是通过 iteratively 标记出合数来找到素数。以下是算法的步骤：

1. 创建一个布尔数组，表示从 0 到 \(Y\) 的每个整数是否为素数。初始时，将 2 到 \(Y\) 的所有值标记为真（假设它们是素数）。
2. 从第一个素数 2 开始，将其倍数标记为合数（非素数）。
3. 找到下一个未标记的数，它就是下一个素数。
4. 重复步骤 2 和 3，直到处理到 \(\sqrt{Y}\)。
5. 剩下的未标记的数即为素数。

以下是用 Python 实现的代码：

```python
def sieve_of_eratosthenes(x, y):
"""找出X和Y之间的所有素数（包含X和Y）"""
if x < 2:
x = 2
is_prime = [True] * (y + 1)
p = 2
while (p * p <= y):
if is_prime[p]:
for i in range(p * p, y + 1, p):
is_prime[i] = False
p += 1
primes = [p for p in range(x, y + 1) if is_prime[p]]
return primes

# 示例使用
X = 10
Y = 50
prime_numbers = sieve_of_eratosthenes(X, Y)
print(f"{X} 和 {Y} 之间的素数有: {prime_numbers}")
```

### 代码说明

1. **数组初始化**：
- 创建一个布尔数组 `is_prime`，大小为 \(Y + 1\)，默认所有数都是素数（标记为 `True`）。

2. **标记合数**：
- 从 2 开始，标记其所有倍数为 `False`。
- 继续下一个未标记的数，重复此过程直到超过 \(\sqrt{Y}\)。

3. **收集素数**：
- 从 \(x\) 到 \(y\) 的范围中，收集所有仍标记为 `True` 的数。

### 优势

埃拉托色尼筛法在处理较大范围的素数查找时表现得更为高效，因为它能有效地减少需要检查的数的数量。对于需要多次查找素数的情况，这个算法尤其适用。

【注3】

### ESFP学生和ENTP老师的课堂讨论对话

#### 课堂场景

**ESFP学生**：老师，我一直对负数（negative numbers）的除法（division）感到困惑。能不能帮我理清楚这个概念？

**ENTP老师**：当然可以！这个问题有趣而且非常重要。我们可以用几个例子（examples）来帮助你理解。准备好了吗？

**ESFP学生**：准备好了！我喜欢通过例子来学习。

#### 例子1：负数除以正数

**ENTP老师**：好，第一个例子：假设我们有 \(-10 \div 2\)。你觉得答案可能是什么？

**ESFP学生**：嗯，我想可能是负数，因为负数除以正数应该还是负数。

**ENTP老师**：完全正确！\(-10 \div 2 = -5\)。这是因为你把 \(-10\) 分成 2 份，每份是 \(-5\)。就像你有 10 个苹果欠人家，每次还 2 个，一共还 5 次。

**ESFP学生**：哦，我明白了！负数除以正数，结果是负数。

#### 例子2：负数除以负数

**ENTP老师**：接下来，考虑 \(-10 \div -2\)。这次会是什么结果呢？

**ESFP学生**：这有点棘手……我想可能是正数？

**ENTP老师**：没错！\(-10 \div -2 = 5\)。因为负负得正，就像这两个负数抵消了。想象一下：你欠 10 个苹果的债务（debt），每次有人帮你还掉 2 个（负数抵消），你最终就没有欠债了。

**ESFP学生**：所以负数除以负数结果是正数。这也有点像减去负数是增加。

#### 例子3：正数除以负数

**ENTP老师**：最后一个例子，看 \((10 \div -2)\)。这次呢？

**ESFP学生**：这应该是负数，因为正数除以负数结果是负数。

**ENTP老师**：对极了！\(10 \div -2 = -5\)。就像你有 10 个苹果，本来准备分给朋友，结果却是借的，每次借 2 个，结果欠了 5 次。

**ESFP学生**：哦，明白了！感觉就像在做数学的“反向操作”。

#### 总结和思维导图

**ENTP老师**：总结一下：负数除法有三种情况：
1. 负数除以正数，结果是负数。
2. 负数除以负数，结果是正数。
3. 正数除以负数，结果是负数。

我们可以用一个思维导图（mind map）来帮助记忆：

```
除法
/ | \
负数 ÷ 正数负数 ÷ 负数正数 ÷ 负数
| | |
结果是负数结果是正数结果是负数
```

**ESFP学生**：这个思维导图太棒了！通过这些例子，我感觉负数除法没那么复杂了。

**ENTP老师**：太好了！记住，数学里很多时候都是通过观察模式（patterns）来理解问题。你现在已经掌握了负数除法的基础。继续保持这种好奇心，数学会越来越有趣！

**ESFP学生**：谢谢老师，我会的！

### ESFP学生和ENTP老师的课堂讨论对话

#### 课堂场景

**ESFP学生**：老师，我在学习负数除法（negative division）时发现余数（remainder）这个概念有点难以理解。特别是涉及负数的时候。

**ENTP老师**：我明白你的困惑。负数的除法和余数确实需要一点时间去适应。我们可以通过几个例子（examples）来深入探讨一下。

**ESFP学生**：好的，我喜欢通过具体的例子来搞清楚问题。

#### 例子1：负数除以正数

**ENTP老师**：想象一下，我们有 \(-10 \div 3\)。商数（quotient）是多少？余数呢？

**ESFP学生**：让我想想，\(-10\) 除以 3，商数应该是 \(-3\)，因为 \(-3 \times 3 = -9\)，那余数就是 \(-10 - (-9) = -1\)。

**ENTP老师**：接近了，不过余数通常是非负的（non-negative），所以我们通常调整商数来使余数非负。在这种情况下，商数可以是 \(-4\)，余数就是 2，因为 \(-10 = (-4) \times 3 + 2\)。

**ESFP学生**：哦，我明白了！我们要调整商数以确保余数是非负的。

#### 例子2：负数除以负数

**ENTP老师**：接下来，看看 \(-10 \div -3\)。这次的商数和余数是什么？

**ESFP学生**：负数除以负数给正数，所以商数应该是 3。然后，\(-10 = 3 \times (-3) - 1\)，那么余数是 \(-1\)？

**ENTP老师**：你推理得很好，不过我们还是要确保余数非负。因此，商数我们调整到 4，这样余数是 2，因为 \(-10 = 4 \times (-3) + 2\)。

**ESFP学生**：明白了！所以无论如何，余数都要是非负的。

#### 例子3：正数除以负数

**ENTP老师**：最后一个例子，看看 \(10 \div -3\)。

**ESFP学生**：这比较简单，商数是 \(-4\)，因为 10 可以被分成 \(-4 \times -3 = 12\)，然后余数是 \(10 - 12 = -2\)。

**ENTP老师**：对的，但是我们需要调整商数让余数非负。商数可以调整为 \(-3\)，这样余数就是 1，因为 \(10 = (-3) \times (-3) + 1\)。

**ESFP学生**：所以余数始终要非负，明白了！

#### Python代码示例

```python
def divide_with_remainder(dividend, divisor):
"""
计算除法的商数和余数，并确保余数为非负。
:param dividend: 被除数 (dividend)
:param divisor: 除数 (divisor)
:return: (商数, 余数)
"""
# 计算商数，使用地板除法，向下取整
quotient = dividend // divisor
# 计算余数
remainder = dividend % divisor

# 如果余数是负数，则调整商和余数
if remainder < 0:
quotient += 1
remainder -= divisor

return quotient, remainder

# 示例调用
examples = [(-10, 3), (-10, -3), (10, -3)]
for dividend, divisor in examples:
q, r = divide_with_remainder(dividend, divisor)
print(f"{dividend} ÷ {divisor} = {q}，余数是 {r}")
```

#### 代码说明

1. **函数定义**：
- `divide_with_remainder` 函数接收两个参数：被除数（dividend）和除数（divisor）。

2. **商数计算**：
- 使用地板除法 `//` 计算初始商数（quotient）。

3. **余数计算**：
- 使用模运算 `%` 计算余数（remainder）。

4. **余数调整**：
- 如果余数为负，调整商数和余数以确保余数为非负。通过增加商数1，并将余数减去除数以获得非负余数。

5. **示例调用**：
- 对每个例子，输出商数和余数。

#### 总结和思维导图

**ENTP老师**：总结一下：

- 负数除法时，确保余数为非负。
- 调整商数以实现这一点。

思维导图如下：

```
负数除法余数
/ | \
负 ÷ 正负 ÷ 负正 ÷ 负
| | |
调整商数，余数非负
```

**ESFP学生**：通过思维导图和代码，我对负数除法的余数理解更清晰了，谢谢老师！

### ESFP学生和ENTP老师的课堂讨论对话

#### 课堂场景

**ESFP学生**：老师，我在编程时遇到了负数除法的取模（modulus）和取余（remainder）的问题。它们有什么区别呢？

**ENTP老师**：这是个很好的问题！取模和取余常常在处理除法时被混淆。它们在计算上有一些细微但重要的区别。我们可以通过一些例子来理解。

**ESFP学生**：好的，我准备好学习这些不同的概念了。

#### 例子1：正数除以正数

**ENTP老师**：首先，我们来看一个简单的例子：\(10 \div 3\)。

- **取模（modulus）**：通常在编程中使用 `%` 操作符。对于正数来说，取模和取余结果是一样的。这里，\(10 \% 3 = 1\)。
- **取余（remainder）**：数学上定义的余数，和取模在正数情况下相同，所以这里也是 1。

**ESFP学生**：所以在正数情况下，取模和取余给我们相同的结果。

#### 例子2：负数除以正数

**ENTP老师**：现在来看 \(-10 \div 3\)。

- **取模（modulus）**：在大多数编程语言中，\(-10 \% 3 = 2\)。这是因为取模的结果符号和除数一致。
- **取余（remainder）**：数学定义中，\(-10\) 除以 3 的余数是 \(-1\)，因为 \(-10 = (-4) \times 3 + 2\)。

**ESFP学生**：哦，我明白了，取模的结果是非负的，而取余的结果可以是负的。

#### 例子3：负数除以负数

**ENTP老师**：最后一个例子：\(-10 \div -3\)。

- **取模（modulus）**：在编程中，\(-10 \% -3 = -1\)。这里，取模结果的符号和除数一致。
- **取余（remainder）**：数学上，\(-10\) 除以 \(-3\) 的余数是 \(-1\)，因为 \(-10 = 3 \times (-3) + (-1)\)。

**ESFP学生**：所以当除数是负数时，取模的结果和除数符号一致，而取余仍然是数学上定义的余数。

#### Python代码示例

```python
def modulus_and_remainder(dividend, divisor):
"""
计算取模和取余的结果。
:param dividend: 被除数 (dividend)
:param divisor: 除数 (divisor)
:return: (模 (modulus), 余数 (remainder))
"""
# 计算模，使用 % 操作符
modulus = dividend % divisor

# 计算余数，使用公式调整模的结果
remainder = dividend - (dividend // divisor) * divisor

return modulus, remainder

# 示例调用
examples = [(10, 3), (-10, 3), (-10, -3)]
for dividend, divisor in examples:
mod, rem = modulus_and_remainder(dividend, divisor)
print(f"{dividend} ÷ {divisor} -> 模 (modulus): {mod}，余数 (remainder): {rem}")
```

#### 代码说明

1. **函数定义**：
- `modulus_and_remainder` 函数接收两个参数：被除数（dividend）和除数（divisor）。

2. **取模计算**：
- 使用 `%` 操作符计算模（modulus）。

3. **取余计算**：
- 使用公式 `dividend - (dividend // divisor) * divisor` 计算数学上的余数（remainder）。

4. **示例调用**：
- 对每个例子，输出取模和取余的结果。

#### 总结和思维导图

**ENTP老师**：总结一下，取模和取余的区别主要在于符号和计算方式：

- **取模**：结果的符号和除数相同。
- **取余**：数学定义的结果，可以是负数。

思维导图如下：

```
负数除法
/ \
取模取余
| |
符号同除数数学定义
```

**ESFP学生**：通过思维导图和代码，我对负数除法的取模和取余有了更清晰的理解。谢谢老师！

取模（modulus）和取余（remainder）在以下情况下会有所不同：