快速排序递归与非递归实现

算法概述：

分而治之。

选出一个元素作为主元，它可以把集合中的元素分成两部分，一部分都是大于它的，一部分都小于它的。

我们先用伪代码描述。

void QuickSort(ElementType A[],int N)
{
   //如果只剩一个元素了直接返回
   if(N<2) return;
   pivot=从A[]选出一个主元;
   将S={ A[]\pivot }分成两个独立的子集;
     A1={ a∈S | a≤ pivot }和A2={ a∈S | a≥ pivot};
   A[]=QuickSort(A1,N1)∪ pivot ∪ QuickSort(A2,N2);
}

选主元

选主元一定要慎重。如果是下面这种情况
共有5个元素，1 2 3 4 5
选1作为主元那么比1小的为空，比1大的有4个。这样进行的快排是一点也不快的。
取头，中，尾的三个元素比较，选出中间大小的元素作为主元

ElementType Median(ElementType A[],int left, int right)
{
   int center=(left+right)/2;
   if(A[left]>A[center])
   {
       Swap(&A[left],&A[center]);
   }
   if(A[left]>A[right])
   {
      Swap(&A[left],&A[right]);
   }
   if(A[center]>A[right])
   {
      Swap(&A[center],&A[right]);
   }
   //将pivot放到right-1的位置，我们知道A[left]肯定小于主元A[right]肯定大于主元
   //只需要考虑A[left+1]~A[right-2]
   Swap(&A[center],&A[right-1]);
   return A[right-1];
}

子集划分

6是主元，被放在最右端。

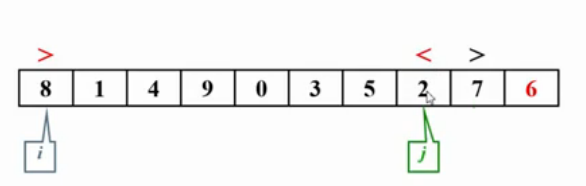
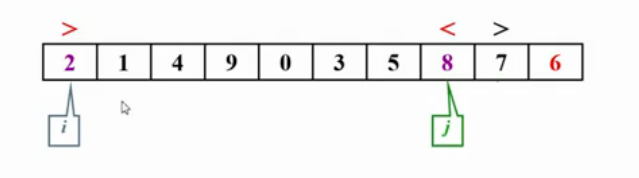
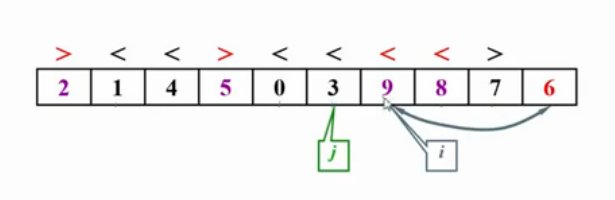
当i对应的元素大于主元，j对应的元素小于主元，停下来，进行交换

当i>j时，停止交换。并把主元与i位置元素交换。选出来的主元，在完成一次子集划分后，主元会被放到最终应在的位置。

小规模数据的处理

因为使用了递归，对于小规模的数据，可能快排还没有如插入排序的简单排序快。
所以我们可以设定一个阈值Cutoff，当递归时的数据规模足够小，我们就停止递归了，直接调用简单排序。

递归

代码：

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<algorithm>
using namespace std;
int median(int* arr, int left, int right){
    int center = (left + right) / 2;
    if (arr[left] > arr[center]){
        swap(arr[left],arr[center]);
    }
    if (arr[left] > arr[right]){
        swap(arr[left],arr[right]);
    }
    if (arr[center] > arr[right]){
        swap(arr[center],arr[right]);
    }
    swap(arr[center],arr[right-1]);
    return arr[right - 1];
}
void insertSort(int* arr,int n){
    int tmp;
    for (int i = 1; i < n; i++){
        tmp = arr[i];
        int j;
        for (j = i; j>0 && arr[j - 1] > tmp; j--){
            arr[j] = arr[j - 1];
        }
        arr[j] = tmp;
    }
}
int cutoff = 5;
void quickSort(int* arr,int left,int right){
    if (cutoff <= (right - left)){
        int pivot = median(arr,left,right);
        int i = left;
        int j = right - 1;
        while (1){
            while (arr[++i] < pivot){
            }
            while (arr[--j]>pivot){
            }
            if (i < j){
                swap(arr[i],arr[j]);
            }
            else{
                break;
            }
        }
        swap(arr[i],arr[right-1]);
        quickSort(arr,left,i-1);
        quickSort(arr,i+1,right);
    }
    else{
        insertSort(arr+left,right-left+1);
    }
}
int main()
{
    int arr[20] = {20,19,18,10,17,16,15,14,13,9,5,6,7,8,1,2,3,11,4,12};
    quickSort(arr,0,19);
    system("pause");
    return 0;
}

非递归，手动利用栈来存储每次分块时快排的起始点。这种写法的执行效率低于递归算法。

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<stack>
using namespace std;
struct Node{
    int low;
    int high;
};//存放待排子列的区间
void insertSort(int* arr, int n){
    int tmp;
    for (int i = 1; i<n; i++){
        tmp = arr[i];
        int j;
        for (j = i; j>0 && arr[j - 1] >= tmp; j--){
            arr[j] = arr[j - 1];
        }
        arr[j] = tmp;
    }
}
int median(int* arr, int left, int right){
    int center = (left + right) / 2;
    if (arr[left] > arr[center]){
        swap(arr[left],arr[center]);
    }
    if (arr[left] > arr[right]){
        swap(arr[left],arr[right]);
    }
    if (arr[center] > arr[right]){
        swap(arr[center],arr[right]);
    }
    swap(arr[center],arr[right-1]);
    return arr[right - 1];
}
int partition(int* arr,int left,int right){
    int pivot = median(arr,left,right);
    int i = left;
    int j = right - 1;
    while (i<j){
        while (arr[++i] < pivot){}
        while (arr[--j] > pivot){}
        if (i < j){
            swap(arr[i],arr[j]);
        }
        else{
            break;
        }
    }
    swap(arr[i],arr[right-1]);
    return i;
}

void quickSort(int* arr,int left,int right){
    stack<Node> s;
    int pivot;
    Node node;
    node.low = left;
    node.high = right;
    s.push(node);
    while (!s.empty()){
        node = s.top();
        s.pop();
        pivot = partition(arr,node.low,node.high);
        if (pivot - 1 > node.low){
            Node node1;
            node1.low = node.low;
            node1.high = pivot - 1;
            s.push(node1);
        }
        if (pivot + 1 < node.high){
            Node node2;
            node2.low = pivot + 1;
            node2.high = node.high;
            s.push(node2);
        }
    }
}
int main()
{
    int arr[20] = { 20, 19, 18, 10, 17, 16, 15, 14, 13, 9, 5, 6, 7, 8, 1, 2, 3, 11, 4, 12 };
    quickSort(arr, 0, 19);
    system("pause");
    return 0;
}