声明：转载随意。
自然常数e，约为2.71828。
e，作为数学常数，是自然对数函数的底数。有时称它为欧拉数（Euler number），以瑞士数学家欧拉命名；
它的其中一个定义是 ，其数值约为（小数点后100位）：“e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274”。
它也等于
。注意，
。
自然常数经常在公式中做指数函数和对数函数的底。
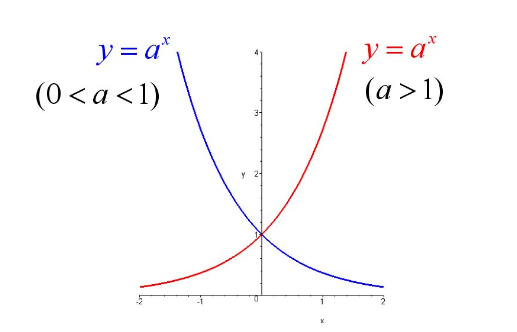
对指数函数和对数函数求导时，就要使用自然常数。
函数
的导数为
。
函数
的导数为
。
参考摘录：http://baike.baidu.com/link?url=iwAX6tx3s2D-U1s3_yaekiydXtulIu8Omv47lHKoegXVEYYhN8i4p5UUAAcV32fnHK37ATA6gEV0g_w5k25ecGmJL3zoUfxIQOPbU1Zwj-hTJlzgxolOsxScvT08IrPw
1903
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
